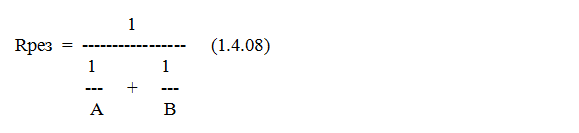Уравнение ОС для экспоненциальной функции. Оос.

Рассмотрим экспоненциальную функцию при ООС. Тогда в блок-схеме на рис. 1.4.9:

p = - η *y - функция обратной передачи (ООС, блок 1), где η = dy/y - коэффициент обратной связи, dy - количество выходного сигнала, подаваемого на входной сумматор,

s = x + p - функция сумматора (блок 2),

y = exp (K * s + B) - функция прямой передачи (блок 3), где К и B - параметры экспоненциальной функции.

Поскольку s = x - η * y, получаем логарифмическое уравнение:

y = exp (K* x – K*η *y + B) (1.4.07).

Теперь сравним формулу (1.4.07) с формулой двухполюсника (1.4.04), представляющего собой включенные последовательно идеальный диод и резистор (см. главу 1.4.2.1):

Ia = exp (K*Ua – K*R_D*Ia + B) (1.4.04).

Мы видим, что коэффициент ООС у нас η = R_D! Функцию ОС можно вычислить через логарифмическое уравнение, применяя алгоритм MidI (см. рис. 1.4.7.,  рис. 1.4.8.). Функция с ООС в подпрограмме MidI представлена для одной переменной.

Реальный полупроводниковый диод моделируется двухполюсником, приведённым на рис. 1.4.5, при этом резистор R_D представляет собой коэффициент, показывающий, какая часть электрического тока будет превращена в тепло. Отсюда можно сделать вывод, что ООС в PN-переходе полупроводникового диода возникает в виде сопротивления R_D, на котором выделяется тепловая энергия (полупроводниковый эффект Зеебека). Эта модель соответствует прямому току диода - прямой ток полупроводникового диода предполагает выделение тепловой энергии на резисторе R_D.

Следует учесть, что логарифмическое уравнение для ВАХ полупроводникового диода в условиях изменения температуры становиться зависимым от 2-х переменных – и температуры, и напряжения.

Определение процессового перехода как функции перехода 2-х процессов, охваченных петлёй ООС.

Моделирование функции, объединяющей два процесса. Процессовый переход.

Очень часто в физике возникает задача построить математическую модель для 2-х процессов, переходящих друг в друга, при изменении аргумента. В радиоэлектронике эти процессы - тепловой и электрический: электрон, являясь носителем и электрической, и тепловой энергии, на равных участвует сразу в этих двух процессах. Рассмотрим математические модели для функции, объединяющей эти 2 процесса.

Функция, моделирующая результирующее сопротивление в схеме с параллельным соединением резисторов.

В качестве примера рассмотрим сначала схему:

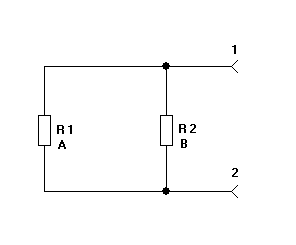
Рис. 1.4.10. Схема двух параллельно соединённых резисторов.

Величина резистора R1 = A, величина резистора R2 = B, где A и B являются некоторыми функциями (процессами). Если величины резисторов R1 = A = const и R2 = B = const, то мы моделируем именно 2 резистора, включенные параллельно. Тогда результирующее сопротивление на разъёмах 1 и 2 определяется известной формулой:

Величины Rрез здесь меньше меньшей величины у резисторов - формула (1.4.08) несёт в себе принцип минимизации результата. По внешнему виду она похожа на рычажные весы, поэтому для краткости будем называть её «формулой весов». Эта формула действительно «взвешивает» две функции A и B и выдаёт результат, меньший меньшего - происходит переход от процесса к процессу по принципу приближения к минимуму от этих двух процессов.

Если параллельные резисторы R1 и R2 имеют ещё и функциональную зависимость от параметра P, то мы получим следующую схему:

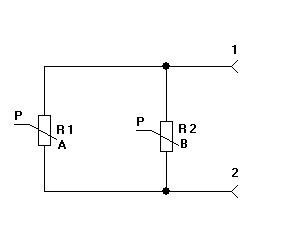
Рис. 1.4.11. Схема двух параллельно соединённых резисторов, функционально зависимых от параметра P (в общем случае A и B - разные функции).

Вариант на рисунке 1.4.11 уже требует дополнительного описания:

величина резистора R1 = A = F1(P),

величина резистора R2 = B = F2(P).

Результирующее значение находим по формуле:

Поскольку функциональные зависимости A и B здесь зависят только от одной переменной P, то такой процессовый переход мы назовём «одномерным».