

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Термоэлектроника – основа для объяснения электронного управления и принципа работы электронных приборов.
Сегодня развитие квантовой механики создало противоречия во всех разделах физики. Примеры:
1. Явления термоэлектронной эмиссии изучаются отдельно от явлений теплопередачи.
2. Явления, происходящие в полупроводниковом диоде, не имеют ничего общего с явлениями в электровакуумном диоде.
3. Закон «3/2» и закон Ричардсона-Дэшмана изучаются отдельно.
4. Явление фотоэффекта изучается отдельно от явлений теплопередачи и термоэлектронной эмиссии.
5. Элементы Пельте изучаются как 2-хэлементные и игнорируется медь как термоэлектрический материал.
6. Токи инжекции не считаются тепловыми токами.
7. Не сформулированы границы применимости правил Киргофа электрической цепи, что создаёт путаницу в теории нелинейных цепей.
8. Управляющие процессы, происходящие в электронных приборах, никак не связаны с тепловыми процессами.
9. Когда изучается транзистор, то сообщается, что электроны преодолевают только электрический барьер, и не сообщается, что электроны преодолевают и тепловой барьер.
10. При передаче тепла фиктивной частицей "фононом" полностью скрываются от исследователя электронно-ядерные взаимодействия.
Всё это необходимо исправить в физике. В данной главе сделана попытка объединить все разделы физики, которые имеют отношение к термоэлектронике. Это первый шаг к созданию новой теории - скорее всего, это будет теория перехода процессов: тепловых и электрических, которая будет построена на основе классической физики и в которой не будет места для квантовой механики. Также недопустимо в новой теории применение всевозможных «статистик» и «распределений», так как это приводит к грубейшим ошибкам. Не зная функций и модели атома, нельзя допускать, чтобы электроны в проводниках и других веществах имели вид идеального газа!
Заключение.
Подведём итог по данной главе:
1. В работе была расширена область применения термоэлектроники.
2. Сделана попытка использовать теорию теплового заряда.
3. Создана новая модель атома, в которой учитывалась теплопередача посредством электронов.
4. Рассмотрены разные виды термоэлектронной эмиссии как процесса теплопередачи.
5. Рассмотрена работа PN-перехода как контакта двух разных веществ, при этом свойства PN-перехода определялись только полярностью термо-ЭДС. В этом смысле термопары уравнивались с полупроводниковыми диодами.
6. Отмечено, что полупроводниковый диод не может называться "кремниевым" или "германиевым" по причине его многослойной конструкции. Также отмечена роль «доноров» и «акцепторов» в создании феномена односторонней проводимости.
7. При рассмотрении транзисторов отмечена асимметрия скрытой электронной эмиссии его PN-переходов.
8. Отмечена связь процессов в полупроводниковом и электровакуумном диоде. Также отмечены ошибки в вопросах исследования электровакуумных диодов.
9. Рассмотрены 2-хэлементные термопарные генераторы термо-ЭДС с точки зрения термоэлектроники. PN-переходы таких генераторов определялись согласно знаку термо-ЭДС.
10. Рассмотрены промышленные "элементы Пельтье", представляющие собой батарею из 3-хэлементных модулей, которая служит генератором «температурного напора». Была отмечена роль меди как термоэлектрического материала, при этом показаны истинные PN-переходы.
1. Элементы термоэлектроники.
1.2. Ошибка в уравнении Шокли для вольт-амперных характеристик прямого тока полупроводниковых диодов.
1.2.1. Графики вольт-амперных характеристик прямого тока полупроводниковых диодов.
Проведём экспериментальные измерения вольт-амперной характеристики (ВАХ) прямого тока кремниевого диода КД213А при температуре 20 градусов Цельсия. График характеристики можно наблюдать в обычном масштабе - ось абсцисс градуируется в Вольтах, ось ординат в Амперах. После построения графика по формуле Шокли можно заметить, что он имеет вид экспоненты. График вольт-амперной характеристики прямого тока обычно имеет вид, подобный графику на рис. 1.2.1:
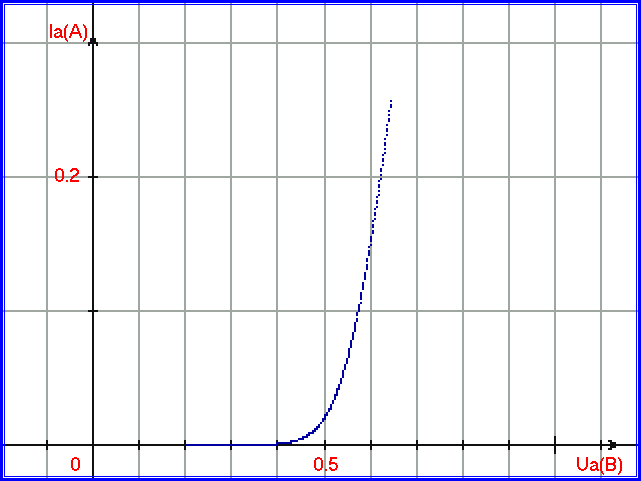 Рис. 1.2.1. Средняя (обычная) ВАХ прямого тока кремниевого полупроводникового диода, измеренная при одной температуре.
Графики экспериментальных измерений построим с помощью точек. График экспериментальной ВАХ прямого тока кремниевого диода КД213А при температуре 20 градусов по Цельсию приведён на рисунке 1.2.2:
Рис. 1.2.1. Средняя (обычная) ВАХ прямого тока кремниевого полупроводникового диода, измеренная при одной температуре.
Графики экспериментальных измерений построим с помощью точек. График экспериментальной ВАХ прямого тока кремниевого диода КД213А при температуре 20 градусов по Цельсию приведён на рисунке 1.2.2:
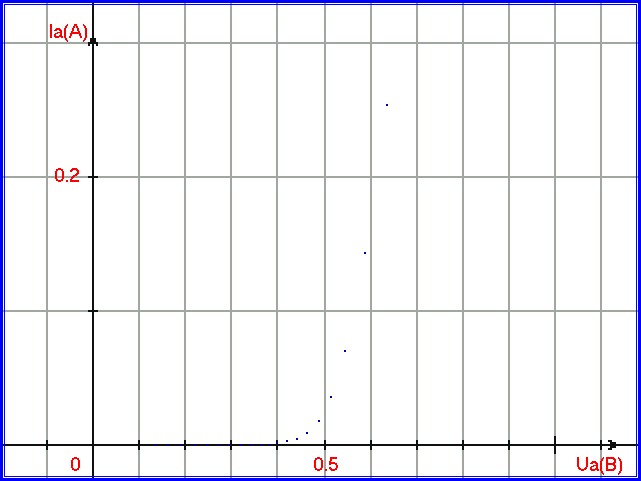 Рис. 1.2.2. График из точек экспериментальных данных вольт-амперной характеристики прямого тока кремниевого диода КД213А.
При наблюдении экспонент для графиков очень удобен полулогарифмический масштаб. Построим тот же график, предварительно прологарифмировав значения тока. Значения тока перед операцией логарифмирования должны быть выражены в Амперах. Логарифмируем в натуральных логарифмах. Простая программа на компьютере легко с этим справится. Если ВАХ диода является идеальной экспонентой, то её графиком в полулогарифмическом масштабе окажется идеальная прямая (уравнение Шокли ВАХ прямого тока и представляет собой такую прямую). На рис. 1.2.3 представлен график обычной ВАХ прямого тока для кремниевого диода в полулогарифмическом масштабе. Ось ординат обозначена как Ln(Ia/1 А) - логарифмировать можно только безразмерную величину, поэтому находим сначала отношение тока анода к одному амперу, после чего производим операцию логарифмирования. Обычно график ВАХ прямого тока в полулогарифмическом масштабе имеет вид, подобный графику на рис. 1.2.3:
Рис. 1.2.2. График из точек экспериментальных данных вольт-амперной характеристики прямого тока кремниевого диода КД213А.
При наблюдении экспонент для графиков очень удобен полулогарифмический масштаб. Построим тот же график, предварительно прологарифмировав значения тока. Значения тока перед операцией логарифмирования должны быть выражены в Амперах. Логарифмируем в натуральных логарифмах. Простая программа на компьютере легко с этим справится. Если ВАХ диода является идеальной экспонентой, то её графиком в полулогарифмическом масштабе окажется идеальная прямая (уравнение Шокли ВАХ прямого тока и представляет собой такую прямую). На рис. 1.2.3 представлен график обычной ВАХ прямого тока для кремниевого диода в полулогарифмическом масштабе. Ось ординат обозначена как Ln(Ia/1 А) - логарифмировать можно только безразмерную величину, поэтому находим сначала отношение тока анода к одному амперу, после чего производим операцию логарифмирования. Обычно график ВАХ прямого тока в полулогарифмическом масштабе имеет вид, подобный графику на рис. 1.2.3:
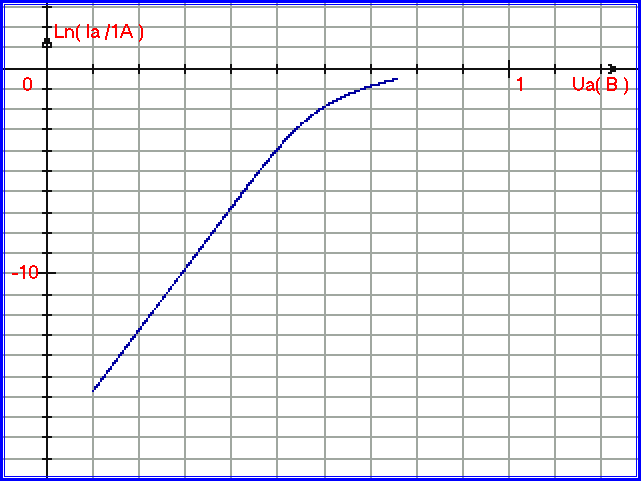 Рис. 1.2.3. Средняя (обычная) ВАХ прямого тока кремниевого полупроводникового диода при одной температуре в полулогарифмическом масштабе.
Построим также график в полулогарифмическом масштабе для точек экспериментальных данных ВАХ прямого тока кремниевого диода КД213А при температуре 20 градусов по Цельсию (рис. 1.2.4):
Рис. 1.2.3. Средняя (обычная) ВАХ прямого тока кремниевого полупроводникового диода при одной температуре в полулогарифмическом масштабе.
Построим также график в полулогарифмическом масштабе для точек экспериментальных данных ВАХ прямого тока кремниевого диода КД213А при температуре 20 градусов по Цельсию (рис. 1.2.4):
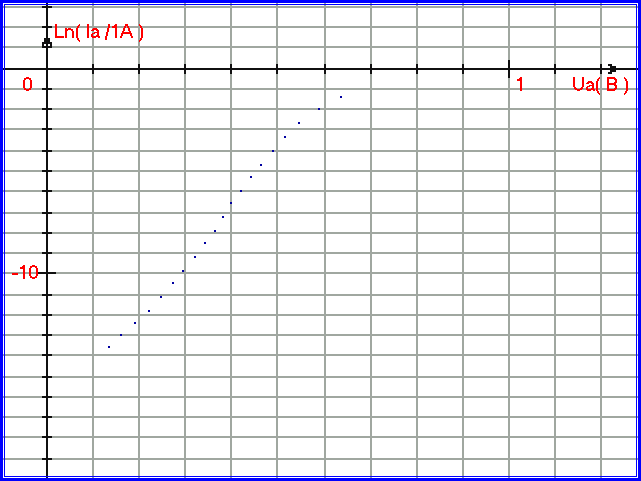 Рис. 1.2.4. График ВАХ прямого тока кремниевого полупроводникового диода КД 213А при температуре 20 градусов по Цельсию в полулогарифмическом масштабе.
На рис. 1.2.4 можно наблюдать, что график имеет изгибы в своей нижней и верхней части, лишь в средней части график похож на прямую линию. Поэтому в данной работе поставлена задача экспериментально проверить, верно ли уравнение Шокли, при этом прямолинейный участок данного графика необходимо выделить и получить для него математическую модель для дальнейшего сравнения с уравнением Шокли.
1.2.2. Моделирование ВАХ прямого тока диода при помощи прямой в полулогарифмическом масштабе.
Определим границы линейного участка по уровням оси ординат:
Рис. 1.2.4. График ВАХ прямого тока кремниевого полупроводникового диода КД 213А при температуре 20 градусов по Цельсию в полулогарифмическом масштабе.
На рис. 1.2.4 можно наблюдать, что график имеет изгибы в своей нижней и верхней части, лишь в средней части график похож на прямую линию. Поэтому в данной работе поставлена задача экспериментально проверить, верно ли уравнение Шокли, при этом прямолинейный участок данного графика необходимо выделить и получить для него математическую модель для дальнейшего сравнения с уравнением Шокли.
1.2.2. Моделирование ВАХ прямого тока диода при помощи прямой в полулогарифмическом масштабе.
Определим границы линейного участка по уровням оси ординат:
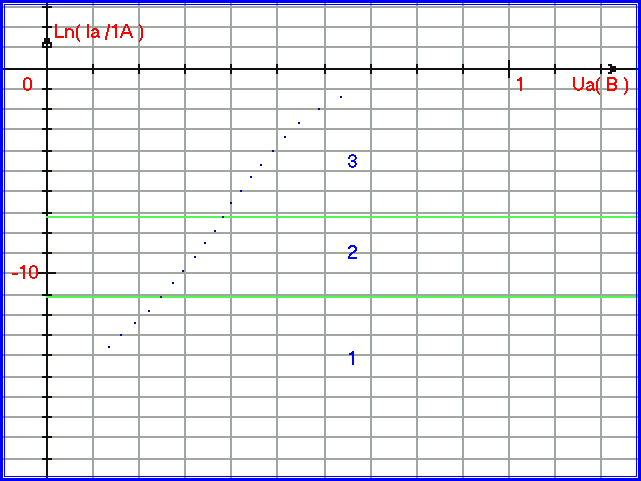 Рис. 1.2.5. 1-й, 2-й и 3-й участки ВАХ прямого тока кремниевого диода КД213А в полулогарифмическом масштабе.
На рис.1.2.5 определён линейный участок (2-й), который ограничен двумя прямыми - они делят плоскость графика на три участка: первый участок – участок малых токов, третий участок – участок больших токов, второй участок - имеет наименьший изгиб, и для него можно построить математическую модель в виде прямой. Математическую модель для участка 2 в полулогарифмическом масштабе можно построить по формуле:
Ln(Ia) = 29,8 • Ua − 18,7
Рис. 1.2.5. 1-й, 2-й и 3-й участки ВАХ прямого тока кремниевого диода КД213А в полулогарифмическом масштабе.
На рис.1.2.5 определён линейный участок (2-й), который ограничен двумя прямыми - они делят плоскость графика на три участка: первый участок – участок малых токов, третий участок – участок больших токов, второй участок - имеет наименьший изгиб, и для него можно построить математическую модель в виде прямой. Математическую модель для участка 2 в полулогарифмическом масштабе можно построить по формуле:
Ln(Ia) = 29,8 • Ua − 18,7
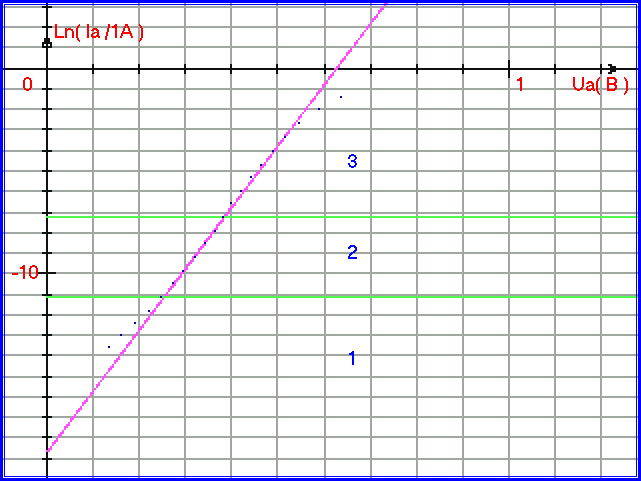 Рис. 1.2.6. Математическая модель 2-го участка ВАХ прямого тока кремниевого диода КД213А в полулогарифмическом масштабе – прямая Ln(Ia)=29,8∙Ua-18,7.
1.2.3. Уравнение Шокли ВАХ прямого тока полупроводникового диода как прямая линия в полулогарифмическом масштабе.
Уравнение Шокли имеет вид:
Iа = Is • (exp((β • e • Uа) / (k • T)) − 1).
Для прямого тока через PN-переход уравнение Шокли имеет вид:
Ia = Is • exp((β • e • Uа) / (k • T)), где:
Is и β — константы (β — некоторый корректирующий коэффициент; выпрямитель называют «идеальным», если β = 1),
e = 1.6 • 10−19 Кл — заряд электрона,
k = 1.38 • 10−23 Дж/ град.С — постоянная Больцмана,
Uа — напряжение на переходе,
T — температура в Кельвинах для 20 град. по Цельсию, т.е. 293 по Кельвину.
Пока нет изменений температуры, приведенная выше математическая модель для КД213А вписывается в уравнение Шокли:
Ln(I) = K • Uа + B.
Ia = exp(K • Uа + B),
где K = (β • e) / (k • T) = β • 39.57065 при T = 293,
B = Ln(Is).
Нам нужно подобрать значение β для обеспечения нужного наклона прямой. Поскольку наша модель описывается уравнением
Ln(Ia) = 29,8 • Ua − 18,7,
то β = 29,8 / 39.57065 = 0,753.
1.2.4. ВАХ двухполюсника - идеального полупроводникового диода, включенного в прямом направлении тока, и резистора.
Диод, ВАХ которого является идеальной экспонентой и описывается уравнением Ia = exp(K • Ua + B), назовём идеальным. Найдём уравнение, которым описывается ВАХ двухполюсника, состоящего из идеального диода VD1 и добавочного резистора RD:
Рис. 1.2.6. Математическая модель 2-го участка ВАХ прямого тока кремниевого диода КД213А в полулогарифмическом масштабе – прямая Ln(Ia)=29,8∙Ua-18,7.
1.2.3. Уравнение Шокли ВАХ прямого тока полупроводникового диода как прямая линия в полулогарифмическом масштабе.
Уравнение Шокли имеет вид:
Iа = Is • (exp((β • e • Uа) / (k • T)) − 1).
Для прямого тока через PN-переход уравнение Шокли имеет вид:
Ia = Is • exp((β • e • Uа) / (k • T)), где:
Is и β — константы (β — некоторый корректирующий коэффициент; выпрямитель называют «идеальным», если β = 1),
e = 1.6 • 10−19 Кл — заряд электрона,
k = 1.38 • 10−23 Дж/ град.С — постоянная Больцмана,
Uа — напряжение на переходе,
T — температура в Кельвинах для 20 град. по Цельсию, т.е. 293 по Кельвину.
Пока нет изменений температуры, приведенная выше математическая модель для КД213А вписывается в уравнение Шокли:
Ln(I) = K • Uа + B.
Ia = exp(K • Uа + B),
где K = (β • e) / (k • T) = β • 39.57065 при T = 293,
B = Ln(Is).
Нам нужно подобрать значение β для обеспечения нужного наклона прямой. Поскольку наша модель описывается уравнением
Ln(Ia) = 29,8 • Ua − 18,7,
то β = 29,8 / 39.57065 = 0,753.
1.2.4. ВАХ двухполюсника - идеального полупроводникового диода, включенного в прямом направлении тока, и резистора.
Диод, ВАХ которого является идеальной экспонентой и описывается уравнением Ia = exp(K • Ua + B), назовём идеальным. Найдём уравнение, которым описывается ВАХ двухполюсника, состоящего из идеального диода VD1 и добавочного резистора RD:
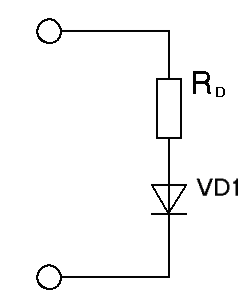 Рис. 1.2.7. Двухполюсник, состоящий из идеального полупроводникового диода и резистора.
Наш идеальный диод VD1 при температуре 20 градусов Цельсия имеет следующее уравнение ВАХ прямого тока (см. выше):
Ln(Ia) = K • Ua + B = 29,8 • Ua − 18,7 (1.2.02).
Запишем уравнение ВАХ прямого тока нашего двухполюсника:
Ua = UD1 + Ur,
где UD1 — напряжение, падающие на идеальном диоде,
Ur — напряжение, падающее на резисторе.
Поскольку
UD1 = (Ln(Ia) − B)/K,
Ur = RD • Ia,
отсюда находим:
Ua = (Ln(Ia) − B) / K + RD • Ia,
Ia = exp(Ua • K - K • RD • Ia + B) (1.2.03)
Получить математическую модель ВАХ двухполюсника можно, решая логарифмическое уравнение (1.2.03) методом подбора. На языке Delphi оно решается при помощи следующей процедуры двоичного поиска:
procedure MidI(Ut, K, B, R: real; var I: real);var Imax, Imin, Up, E: real;begin E:= 0.00001; Imax:= exp(Ut * K + B); Imin:= 0; repeat begin I:= (Imax + Imin) / 2; Up:= I * R + (ln(I) − B) / K; if Up > Ut then Imax:= I else Imin:= I; end until (Up + E > Ut) and (Up − E < Ut);end; Решение логарифмического уравнения (1.2.03) в 20 точках при условии RD = 0,25 Ом позволит нам получить модель 2-го и 3-го участков ВАХ диода КД213А (построена светло-зелёными точками на рис. 1.2.8):
Рис. 1.2.7. Двухполюсник, состоящий из идеального полупроводникового диода и резистора.
Наш идеальный диод VD1 при температуре 20 градусов Цельсия имеет следующее уравнение ВАХ прямого тока (см. выше):
Ln(Ia) = K • Ua + B = 29,8 • Ua − 18,7 (1.2.02).
Запишем уравнение ВАХ прямого тока нашего двухполюсника:
Ua = UD1 + Ur,
где UD1 — напряжение, падающие на идеальном диоде,
Ur — напряжение, падающее на резисторе.
Поскольку
UD1 = (Ln(Ia) − B)/K,
Ur = RD • Ia,
отсюда находим:
Ua = (Ln(Ia) − B) / K + RD • Ia,
Ia = exp(Ua • K - K • RD • Ia + B) (1.2.03)
Получить математическую модель ВАХ двухполюсника можно, решая логарифмическое уравнение (1.2.03) методом подбора. На языке Delphi оно решается при помощи следующей процедуры двоичного поиска:
procedure MidI(Ut, K, B, R: real; var I: real);var Imax, Imin, Up, E: real;begin E:= 0.00001; Imax:= exp(Ut * K + B); Imin:= 0; repeat begin I:= (Imax + Imin) / 2; Up:= I * R + (ln(I) − B) / K; if Up > Ut then Imax:= I else Imin:= I; end until (Up + E > Ut) and (Up − E < Ut);end; Решение логарифмического уравнения (1.2.03) в 20 точках при условии RD = 0,25 Ом позволит нам получить модель 2-го и 3-го участков ВАХ диода КД213А (построена светло-зелёными точками на рис. 1.2.8):
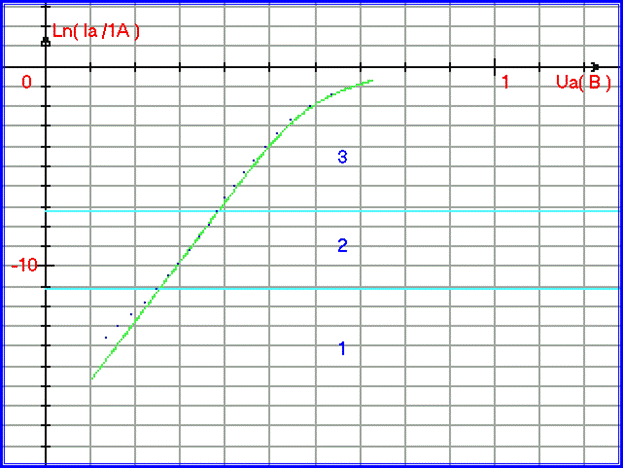 Рис. 1.2.8. Математическая модель 2-го и 3-го участков ВАХ прямого тока кремниевого диода КД213А в полулогарифмическом масштабе.
1.2.5. Зависимость ВАХ прямого тока диода от температуры согласно уравнения Шокли.
Построим ВАХ при изменении температуры согласно уравнению Шокли. Для прямого тока PN-перехода уравнение Шокли имеет вид:
Iа = Is • exp((β • e • Uа) / (k • T))
Если выразить его как:
Iа = exp(K • Uа + B),
тогда:
K = (β • e) / (k • T) = β • 39.57065 при T = 293,
B = Ln(Is).
Для диода КД213А найдено:
β = 0,753
K =29,8
B = −18,7
Параметр B не должен влиять на наклон прямой. В современных моделях этот параметр вдруг становиться температурно-зависимым, что неверно - он не должен влиять на наклон прямой, иначе он становится зависимым и от Uа, температура в уравнении Шокли определена только в знаменателе выражения (β • e) / (k • T). Построим графики по формуле Шокли для температур 10, 20 и 30 градусов по Цельсию для диода КД213А, считая параметр В на заданном участке температур неизменным и равным −18,7. На рис. 1.2.9. по формуле Шокли построены графики для температур -20, 20 и 60 градусов по Цельсию для диода КД213А (график для температур -20 градусов Цельсия показан синими точками, 20 градусов — зелёным, 60 градусов — красным). Графики построены поверх ВАХ экспериментальных данных для диода КД213А при 20 град. Цельсия (синие точки):
Рис. 1.2.8. Математическая модель 2-го и 3-го участков ВАХ прямого тока кремниевого диода КД213А в полулогарифмическом масштабе.
1.2.5. Зависимость ВАХ прямого тока диода от температуры согласно уравнения Шокли.
Построим ВАХ при изменении температуры согласно уравнению Шокли. Для прямого тока PN-перехода уравнение Шокли имеет вид:
Iа = Is • exp((β • e • Uа) / (k • T))
Если выразить его как:
Iа = exp(K • Uа + B),
тогда:
K = (β • e) / (k • T) = β • 39.57065 при T = 293,
B = Ln(Is).
Для диода КД213А найдено:
β = 0,753
K =29,8
B = −18,7
Параметр B не должен влиять на наклон прямой. В современных моделях этот параметр вдруг становиться температурно-зависимым, что неверно - он не должен влиять на наклон прямой, иначе он становится зависимым и от Uа, температура в уравнении Шокли определена только в знаменателе выражения (β • e) / (k • T). Построим графики по формуле Шокли для температур 10, 20 и 30 градусов по Цельсию для диода КД213А, считая параметр В на заданном участке температур неизменным и равным −18,7. На рис. 1.2.9. по формуле Шокли построены графики для температур -20, 20 и 60 градусов по Цельсию для диода КД213А (график для температур -20 градусов Цельсия показан синими точками, 20 градусов — зелёным, 60 градусов — красным). Графики построены поверх ВАХ экспериментальных данных для диода КД213А при 20 град. Цельсия (синие точки):
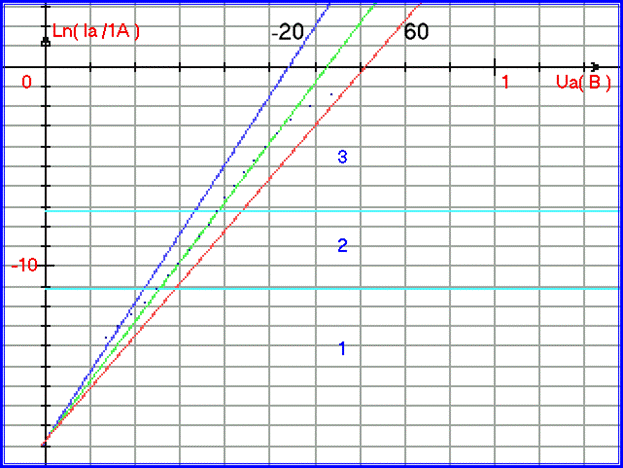 Рис. 1.2.9. Зависимость ВАХ от температуры согласно уравнения Шокли (графики построены поверх экспериментальных данных в полулогарифмическом масштабе).
Изучая зависимость ВАХ прямого тока от температуры согласно уравнения Шокли, можно сделать выводы:
Рис. 1.2.9. Зависимость ВАХ от температуры согласно уравнения Шокли (графики построены поверх экспериментальных данных в полулогарифмическом масштабе).
Изучая зависимость ВАХ прямого тока от температуры согласно уравнения Шокли, можно сделать выводы:
- Графики уравнения Шокли имеют вид расширяющегося пучка прямых от точки, расположенной на оси ординат.
- Более низкие температуры соответствуют более высокому току при одном и том же Ua.
Проведённые в дальнейшем эксперименты с ВАХ в зависимости от температур показывают, что данные свойства уравнения Шокли не соответствуют свойствам ВАХ реальных полупроводниковых диодов. На рис. 1.2.10 приведены графики ВАХ экспериментальных данных диода КД 213А для температуры 10 градусов Цельсия (выполнен синим цветом) и температуры 60 градусов Цельсия (показан красным цветом). Стрелкой указано направление смещения ВАХ при нагревании - такое смещение соответствует реальности (при наблюдении эксперимента):
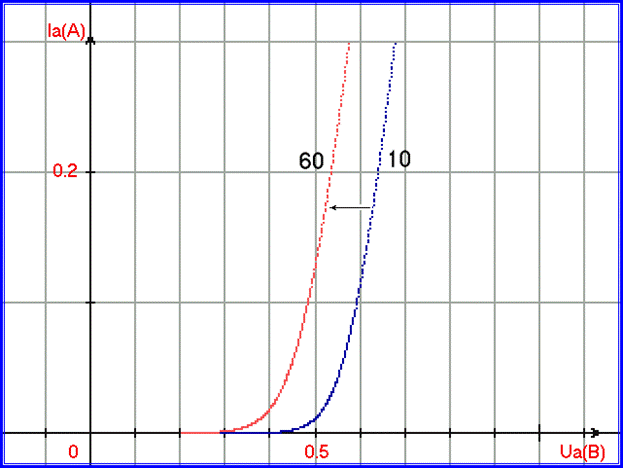 Рис. 1.2.10. Смещение ВАХ диода при нагревании, наблюдаемое при физическом эксперименте (стрелкой указано направление смещения).
На рис. 1.2.11 приведены графики ВАХ диода КД 213А, построенных по формуле Шокли для температуры 10 градусов по Цельсию (выполнен синим цветом) и температуры 60 градусов по Цельсию (выполнен красным цветом). Стрелкой указано направление смещения ВАХ при нагревании, которое не соответствует реальности (при наблюдении физического эксперимента):
Рис. 1.2.10. Смещение ВАХ диода при нагревании, наблюдаемое при физическом эксперименте (стрелкой указано направление смещения).
На рис. 1.2.11 приведены графики ВАХ диода КД 213А, построенных по формуле Шокли для температуры 10 градусов по Цельсию (выполнен синим цветом) и температуры 60 градусов по Цельсию (выполнен красным цветом). Стрелкой указано направление смещения ВАХ при нагревании, которое не соответствует реальности (при наблюдении физического эксперимента):
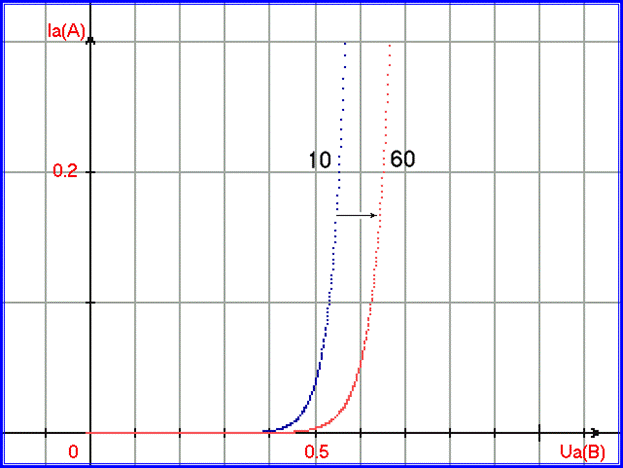 Рис. 1.2.11. Смещение ВАХ прямого тока диода при нагревании, соответствующее уравнению Шокли.
Из приведённых наблюдений можно сделать вывод, что уравнение Шокли для ВАХ прямого тока полупроводникового диода неверно.
1.2.6. Зависимость ВАХ прямого тока от температуры, наблюдаемая в эксперименте, и расчёт математической модели.
Исследуем ВАХ прямого тока при изменении температуры. Для этого измерим ВАХ прямого тока кремниевого диода КД213А при температурах 10, 20, 30, 40, 50, 60 градусов Цельсия. На рис. 1.2.12 построим графики экспериментальных данных в полулогарифмическом масштабе. Точки ВАХ имеют цвет:
Рис. 1.2.11. Смещение ВАХ прямого тока диода при нагревании, соответствующее уравнению Шокли.
Из приведённых наблюдений можно сделать вывод, что уравнение Шокли для ВАХ прямого тока полупроводникового диода неверно.
1.2.6. Зависимость ВАХ прямого тока от температуры, наблюдаемая в эксперименте, и расчёт математической модели.
Исследуем ВАХ прямого тока при изменении температуры. Для этого измерим ВАХ прямого тока кремниевого диода КД213А при температурах 10, 20, 30, 40, 50, 60 градусов Цельсия. На рис. 1.2.12 построим графики экспериментальных данных в полулогарифмическом масштабе. Точки ВАХ имеют цвет:
- ВАХ при температуре 10 градусов Цельсия — зелёный,
- ВАХ при температуре 20 градусов Цельсия — синий,
- ВАХ при температуре 30 градусов Цельсия — красный,
- ВАХ при температуре 40 градусов Цельсия — голубой,
- ВАХ при температуре 50 градусов Цельсия — розовый,
- ВАХ при температуре 60 градусов Цельсия — светло-зелёный,
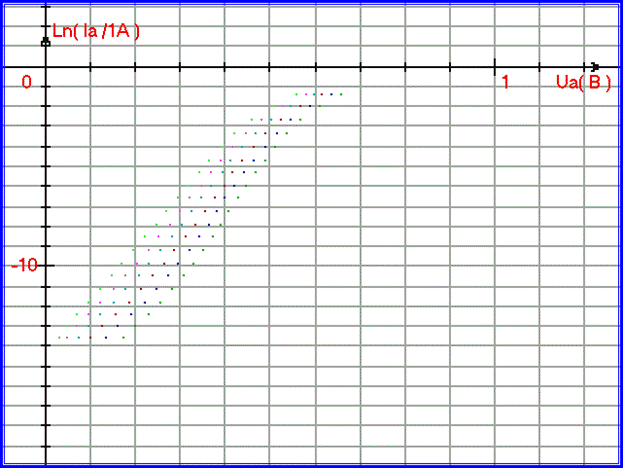 Рис. 1.2.12. Экспериментальные зависимости ВАХ от температуры для диода КД213А (графики построены в полулогарифмическом масштабе).
Рис. 1.2.12. Экспериментальные зависимости ВАХ от температуры для диода КД213А (графики построены в полулогарифмическом масштабе).
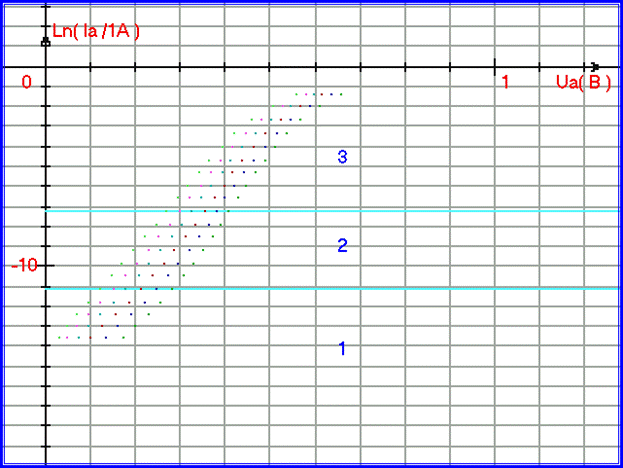 Рис. 1.2.13. Экспериментальные зависимости ВАХ от температуры для диода КД213А (графики построены в полулогарифмическом масштабе). На графике отмечены 3 характерные области участков ВАХ.
Посмотрим на ВАХ на 2-м участке (см. рис. 1.2.13.):
Рис. 1.2.13. Экспериментальные зависимости ВАХ от температуры для диода КД213А (графики построены в полулогарифмическом масштабе). На графике отмечены 3 характерные области участков ВАХ.
Посмотрим на ВАХ на 2-м участке (см. рис. 1.2.13.):
- Графики экспериментальных данных при росте Ua на участке 2 имеют вид сужающегося пучка прямых.
- Более высокие температуры на участке 2 соответствуют более высокому току при одном и том же Ua.
Построив касательные к семейству ВАХ диода КД213А на участке 2, мы обнаружим, что экспериментальные ВАХ представляют собой сужающийся пучок прямых. Найдём уравнение (математическую модель) для пучка этих прямых в зависимости от воздействия температуры на кремниевый диод КД213А на участке 2:
(Ia/1А) = exp(KT • (TF • (Ua − UB) − T • (Ua − UF))) (1.2.04),
где Ia — ток через открытый переход в Амперах,
Ua — напряжение на открытом переходе в Вольтах,
T — температура в Кельвинах,
KT — коэффициент с размерностью Вольт-1•Кельвин-1,
TF — параметр, имеющий размерность температуры в Кельвинах,
UB — параметр, имеющий размерность напряжения в Вольтах,
UF — параметр, имеющий размерность напряжения в Вольтах..
После подстановки этих параметров в уравнение можно получить зависимые от температуры значения параметров прямой:
Ln(Ia/1А) = (K2 • Ua + B2),
где:
K2 = KT • (TF − T) (1.2.05)
B2 = KT • (T • UF − TF • UB) (1.2.06)
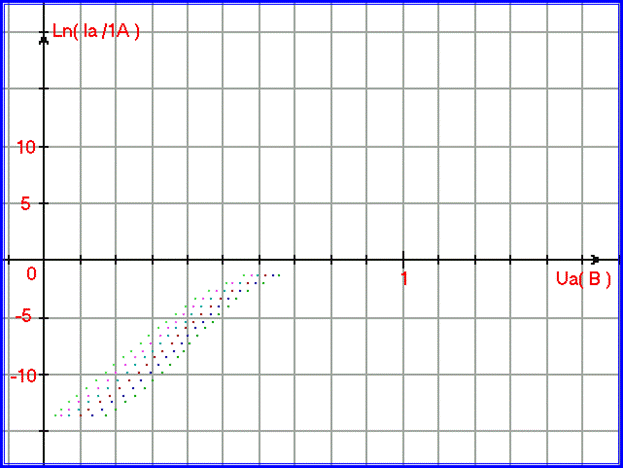 Рис. 1.2.14. То же, что и на рисунке 1.2.13, но в другом масштабе.
Изменение температуры вызывает изменение параметров K2 и B2 прямых. Проведя расчеты для диода КД213А, получим следующие коэффициенты математической модели на 2-м участке ВАХ:
KT = 0,0956 Вольт-1•Кельвин-1,
TF = 605,2 Kельвин,
UF = 1,161 Вольт,
UB = 0,885 Вольт.
Рис. 1.2.14. То же, что и на рисунке 1.2.13, но в другом масштабе.
Изменение температуры вызывает изменение параметров K2 и B2 прямых. Проведя расчеты для диода КД213А, получим следующие коэффициенты математической модели на 2-м участке ВАХ:
KT = 0,0956 Вольт-1•Кельвин-1,
TF = 605,2 Kельвин,
UF = 1,161 Вольт,
UB = 0,885 Вольт.
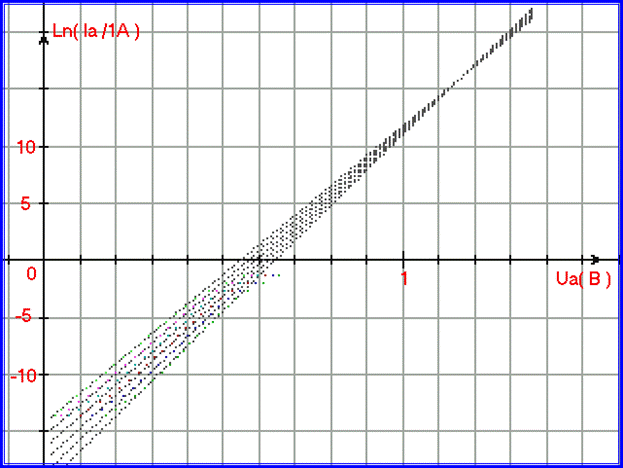 Рис. 1.2.15. Иллюстрация совпадения пучка прямых по новой формуле (1.2.07) и 2-го участка экспериментальных данных для диода КД213А.
На рис. 1.2.15 показаны графики новой математической модели ВАХ диода КД213А:
Ln(Ia/1А) = KT • (T • (UF − Ua) + TF • (Ua − UB)) (1.2.07);
где KT = 0,0956 Вольт-1•Кельвин-1,
TF = 605,2 Kельвин,
UB = 0,885 Вольт,
UF = 1,161 Вольт,
Она почти в точности соответствует сужающемуся пучку прямых (на рис. 1.2.15 видно совпадение модели - серые точки - с экспериментальными данными на 2-м участке ВАХ).
Объединив методы моделирования на 2-м и 3-м участке (см. главу 1.2.4) с учётом температурного воздействия, получим улучшенную математическую модель. Расчёты выполнялись на ЭВМ в системе программирования Delphi с применением процедуры двоичного поиска MidI. Добавочный резистор RD диода КД213А имеет величину RD=0,25 Ом:
Рис. 1.2.15. Иллюстрация совпадения пучка прямых по новой формуле (1.2.07) и 2-го участка экспериментальных данных для диода КД213А.
На рис. 1.2.15 показаны графики новой математической модели ВАХ диода КД213А:
Ln(Ia/1А) = KT • (T • (UF − Ua) + TF • (Ua − UB)) (1.2.07);
где KT = 0,0956 Вольт-1•Кельвин-1,
TF = 605,2 Kельвин,
UB = 0,885 Вольт,
UF = 1,161 Вольт,
Она почти в точности соответствует сужающемуся пучку прямых (на рис. 1.2.15 видно совпадение модели - серые точки - с экспериментальными данными на 2-м участке ВАХ).
Объединив методы моделирования на 2-м и 3-м участке (см. главу 1.2.4) с учётом температурного воздействия, получим улучшенную математическую модель. Расчёты выполнялись на ЭВМ в системе программирования Delphi с применением процедуры двоичного поиска MidI. Добавочный резистор RD диода КД213А имеет величину RD=0,25 Ом:
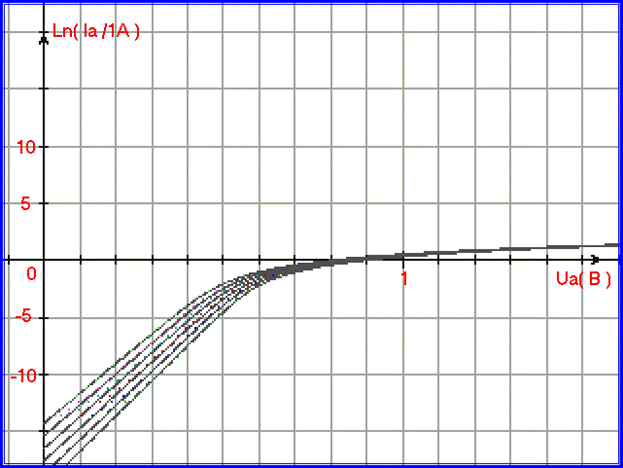 Рис. 1.2.16. Иллюстрация совпадения мат. модели, построенной по формулам (1.1.8.,04), (1.1.6.,02), для 2-го и 3-го участков и экспериментальных данных ВАХ прямого тока диода КД213А (графики построены в полулогарифмическом масштабе).
На рис. 1.2.16. график математической модели построен серыми точками поверх точек экспериментальных данных. Цвет точек экспериментальных данных:
Рис. 1.2.16. Иллюстрация совпадения мат. модели, построенной по формулам (1.1.8.,04), (1.1.6.,02), для 2-го и 3-го участков и экспериментальных данных ВАХ прямого тока диода КД213А (графики построены в полулогарифмическом масштабе).
На рис. 1.2.16. график математической модели построен серыми точками поверх точек экспериментальных данных. Цвет точек экспериментальных данных:
- ВАХ при температуре 10 градусов Цельсия — зелёный,
- ВАХ при температуре 20 градусов Цельсия — синий,
- ВАХ при температуре 30 градусов Цельсия — красный,
- ВАХ при температуре 40 градусов Цельсия — голубой,
- ВАХ при температуре 50 градусов Цельсия — розовый,
- ВАХ при температуре 60 градусов Цельсия — светло-зелёный.
При дальнейшей доработке на базе данной математической модели было получено новое уравнение для ВАХ полупроводникового диода, называемое "эмиссионным уравнением". Его можно вывести, применяя теорию теплового заряда (см. далее).
1.2.7. Заключение
После вывода своего уравнения для ВАХ полупроводникового диода Шокли должен был экспериментально проверить его и дать свою оценку, однако этот этап работы не был проделан. Между тем, многие источники указывают, что уравнение Шокли соответсвует эксперименту. В данной работе было проведено экспериментальное исследование, которое показало неверность уравнения Шокли.
Итоги данной главы:
- Первоначально проведён эксперимент — измерение ВАХ при температуре 20 градусов Цельсия.
- Для математического моделирования ВАХ полупроводникового диода выделены 3 её участка.
- Построена математическая модель 2-го участка.
- Представлено уравнение Шокли для прямого тока.
- Для моделирования 3-го участка использовалась схема последовательного соединения идеального диода и резистора - математическая модель этой цепи описывалась неявным логарифмическим уравнением.
- Приведён алгоритм решения неявного логарифмического уравнения.
- Создана математическая модель ВАХ, объединяющая 2-й и 3-й участок.
- Исследована математическая модель на основе уравнения Шокли при изменении температуры.
- Проведён эксперимент — измерение ВАХ в зависимости от температуры.
- При сравнении математической модели на основе уравнения Шокли при различных температурах и экспериментальных данных обнаружено их несоответствие и сделан вывод, что формула Шокли неверна.
- Создана эмпирическая математическая модель, которая достаточно точно описывает 2-й и 3-й участки ВАХ полупроводникового диода для температур окружающей среды от 10 до 60 градусов Цельсия. Эта математическая модель явилась первым шагом для создания эмиссионнного уравнения.
|
|
|
Элементы термоэлектроники
|



 Рис. 1.2.1. Средняя (обычная) ВАХ прямого тока кремниевого полупроводникового диода, измеренная при одной температуре.
Графики экспериментальных измерений построим с помощью точек. График экспериментальной ВАХ прямого тока кремниевого диода КД213А при температуре 20 градусов по Цельсию приведён на рисунке 1.2.2:
Рис. 1.2.1. Средняя (обычная) ВАХ прямого тока кремниевого полупроводникового диода, измеренная при одной температуре.
Графики экспериментальных измерений построим с помощью точек. График экспериментальной ВАХ прямого тока кремниевого диода КД213А при температуре 20 градусов по Цельсию приведён на рисунке 1.2.2:
 Рис. 1.2.2. График из точек экспериментальных данных вольт-амперной характеристики прямого тока кремниевого диода КД213А.
При наблюдении экспонент для графиков очень удобен полулогарифмический масштаб. Построим тот же график, предварительно прологарифмировав значения тока. Значения тока перед операцией логарифмирования должны быть выражены в Амперах. Логарифмируем в натуральных логарифмах. Простая программа на компьютере легко с этим справится. Если ВАХ диода является идеальной экспонентой, то её графиком в полулогарифмическом масштабе окажется идеальная прямая (уравнение Шокли ВАХ прямого тока и представляет собой такую прямую). На рис. 1.2.3 представлен график обычной ВАХ прямого тока для кремниевого диода в полулогарифмическом масштабе. Ось ординат обозначена как Ln(Ia/1 А) - логарифмировать можно только безразмерную величину, поэтому находим сначала отношение тока анода к одному амперу, после чего производим операцию логарифмирования. Обычно график ВАХ прямого тока в полулогарифмическом масштабе имеет вид, подобный графику на рис. 1.2.3:
Рис. 1.2.2. График из точек экспериментальных данных вольт-амперной характеристики прямого тока кремниевого диода КД213А.
При наблюдении экспонент для графиков очень удобен полулогарифмический масштаб. Построим тот же график, предварительно прологарифмировав значения тока. Значения тока перед операцией логарифмирования должны быть выражены в Амперах. Логарифмируем в натуральных логарифмах. Простая программа на компьютере легко с этим справится. Если ВАХ диода является идеальной экспонентой, то её графиком в полулогарифмическом масштабе окажется идеальная прямая (уравнение Шокли ВАХ прямого тока и представляет собой такую прямую). На рис. 1.2.3 представлен график обычной ВАХ прямого тока для кремниевого диода в полулогарифмическом масштабе. Ось ординат обозначена как Ln(Ia/1 А) - логарифмировать можно только безразмерную величину, поэтому находим сначала отношение тока анода к одному амперу, после чего производим операцию логарифмирования. Обычно график ВАХ прямого тока в полулогарифмическом масштабе имеет вид, подобный графику на рис. 1.2.3:
 Рис. 1.2.3. Средняя (обычная) ВАХ прямого тока кремниевого полупроводникового диода при одной температуре в полулогарифмическом масштабе.
Построим также график в полулогарифмическом масштабе для точек экспериментальных данных ВАХ прямого тока кремниевого диода КД213А при температуре 20 градусов по Цельсию (рис. 1.2.4):
Рис. 1.2.3. Средняя (обычная) ВАХ прямого тока кремниевого полупроводникового диода при одной температуре в полулогарифмическом масштабе.
Построим также график в полулогарифмическом масштабе для точек экспериментальных данных ВАХ прямого тока кремниевого диода КД213А при температуре 20 градусов по Цельсию (рис. 1.2.4):
 Рис. 1.2.4. График ВАХ прямого тока кремниевого полупроводникового диода КД 213А при температуре 20 градусов по Цельсию в полулогарифмическом масштабе.
На рис. 1.2.4 можно наблюдать, что график имеет изгибы в своей нижней и верхней части, лишь в средней части график похож на прямую линию. Поэтому в данной работе поставлена задача экспериментально проверить, верно ли уравнение Шокли, при этом прямолинейный участок данного графика необходимо выделить и получить для него математическую модель для дальнейшего сравнения с уравнением Шокли.
1.2.2. Моделирование ВАХ прямого тока диода при помощи прямой в полулогарифмическом масштабе.
Определим границы линейного участка по уровням оси ординат:
Рис. 1.2.4. График ВАХ прямого тока кремниевого полупроводникового диода КД 213А при температуре 20 градусов по Цельсию в полулогарифмическом масштабе.
На рис. 1.2.4 можно наблюдать, что график имеет изгибы в своей нижней и верхней части, лишь в средней части график похож на прямую линию. Поэтому в данной работе поставлена задача экспериментально проверить, верно ли уравнение Шокли, при этом прямолинейный участок данного графика необходимо выделить и получить для него математическую модель для дальнейшего сравнения с уравнением Шокли.
1.2.2. Моделирование ВАХ прямого тока диода при помощи прямой в полулогарифмическом масштабе.
Определим границы линейного участка по уровням оси ординат:
 Рис. 1.2.5. 1-й, 2-й и 3-й участки ВАХ прямого тока кремниевого диода КД213А в полулогарифмическом масштабе.
На рис.1.2.5 определён линейный участок (2-й), который ограничен двумя прямыми - они делят плоскость графика на три участка: первый участок – участок малых токов, третий участок – участок больших токов, второй участок - имеет наименьший изгиб, и для него можно построить математическую модель в виде прямой. Математическую модель для участка 2 в полулогарифмическом масштабе можно построить по формуле:
Ln(Ia) = 29,8 • Ua − 18,7
Рис. 1.2.5. 1-й, 2-й и 3-й участки ВАХ прямого тока кремниевого диода КД213А в полулогарифмическом масштабе.
На рис.1.2.5 определён линейный участок (2-й), который ограничен двумя прямыми - они делят плоскость графика на три участка: первый участок – участок малых токов, третий участок – участок больших токов, второй участок - имеет наименьший изгиб, и для него можно построить математическую модель в виде прямой. Математическую модель для участка 2 в полулогарифмическом масштабе можно построить по формуле:
Ln(Ia) = 29,8 • Ua − 18,7
 Рис. 1.2.6. Математическая модель 2-го участка ВАХ прямого тока кремниевого диода КД213А в полулогарифмическом масштабе – прямая Ln(Ia)=29,8∙Ua-18,7.
1.2.3. Уравнение Шокли ВАХ прямого тока полупроводникового диода как прямая линия в полулогарифмическом масштабе.
Уравнение Шокли имеет вид:
Iа = Is • (exp((β • e • Uа) / (k • T)) − 1).
Для прямого тока через PN-переход уравнение Шокли имеет вид:
Ia = Is • exp((β • e • Uа) / (k • T)), где:
Is и β — константы (β — некоторый корректирующий коэффициент; выпрямитель называют «идеальным», если β = 1),
e = 1.6 • 10−19 Кл — заряд электрона,
k = 1.38 • 10−23 Дж/ град.С — постоянная Больцмана,
Uа — напряжение на переходе,
T — температура в Кельвинах для 20 град. по Цельсию, т.е. 293 по Кельвину.
Пока нет изменений температуры, приведенная выше математическая модель для КД213А вписывается в уравнение Шокли:
Ln(I) = K • Uа + B.
Ia = exp(K • Uа + B),
где K = (β • e) / (k • T) = β • 39.57065 при T = 293,
B = Ln(Is).
Нам нужно подобрать значение β для обеспечения нужного наклона прямой. Поскольку наша модель описывается уравнением
Ln(Ia) = 29,8 • Ua − 18,7,
то β = 29,8 / 39.57065 = 0,753.
1.2.4. ВАХ двухполюсника - идеального полупроводникового диода, включенного в прямом направлении тока, и резистора.
Диод, ВАХ которого является идеальной экспонентой и описывается уравнением Ia = exp(K • Ua + B), назовём идеальным. Найдём уравнение, которым описывается ВАХ двухполюсника, состоящего из идеального диода VD1 и добавочного резистора RD:
Рис. 1.2.6. Математическая модель 2-го участка ВАХ прямого тока кремниевого диода КД213А в полулогарифмическом масштабе – прямая Ln(Ia)=29,8∙Ua-18,7.
1.2.3. Уравнение Шокли ВАХ прямого тока полупроводникового диода как прямая линия в полулогарифмическом масштабе.
Уравнение Шокли имеет вид:
Iа = Is • (exp((β • e • Uа) / (k • T)) − 1).
Для прямого тока через PN-переход уравнение Шокли имеет вид:
Ia = Is • exp((β • e • Uа) / (k • T)), где:
Is и β — константы (β — некоторый корректирующий коэффициент; выпрямитель называют «идеальным», если β = 1),
e = 1.6 • 10−19 Кл — заряд электрона,
k = 1.38 • 10−23 Дж/ град.С — постоянная Больцмана,
Uа — напряжение на переходе,
T — температура в Кельвинах для 20 град. по Цельсию, т.е. 293 по Кельвину.
Пока нет изменений температуры, приведенная выше математическая модель для КД213А вписывается в уравнение Шокли:
Ln(I) = K • Uа + B.
Ia = exp(K • Uа + B),
где K = (β • e) / (k • T) = β • 39.57065 при T = 293,
B = Ln(Is).
Нам нужно подобрать значение β для обеспечения нужного наклона прямой. Поскольку наша модель описывается уравнением
Ln(Ia) = 29,8 • Ua − 18,7,
то β = 29,8 / 39.57065 = 0,753.
1.2.4. ВАХ двухполюсника - идеального полупроводникового диода, включенного в прямом направлении тока, и резистора.
Диод, ВАХ которого является идеальной экспонентой и описывается уравнением Ia = exp(K • Ua + B), назовём идеальным. Найдём уравнение, которым описывается ВАХ двухполюсника, состоящего из идеального диода VD1 и добавочного резистора RD:
 Рис. 1.2.7. Двухполюсник, состоящий из идеального полупроводникового диода и резистора.
Наш идеальный диод VD1 при температуре 20 градусов Цельсия имеет следующее уравнение ВАХ прямого тока (см. выше):
Ln(Ia) = K • Ua + B = 29,8 • Ua − 18,7 (1.2.02).
Запишем уравнение ВАХ прямого тока нашего двухполюсника:
Ua = UD1 + Ur,
где UD1 — напряжение, падающие на идеальном диоде,
Ur — напряжение, падающее на резисторе.
Поскольку
UD1 = (Ln(Ia) − B)/K,
Ur = RD • Ia,
отсюда находим:
Ua = (Ln(Ia) − B) / K + RD • Ia,
Ia = exp(Ua • K - K • RD • Ia + B) (1.2.03)
Получить математическую модель ВАХ двухполюсника можно, решая логарифмическое уравнение (1.2.03) методом подбора. На языке Delphi оно решается при помощи следующей процедуры двоичного поиска:
procedure MidI(Ut, K, B, R: real; var I: real);var Imax, Imin, Up, E: real;begin E:= 0.00001; Imax:= exp(Ut * K + B); Imin:= 0; repeat begin I:= (Imax + Imin) / 2; Up:= I * R + (ln(I) − B) / K; if Up > Ut then Imax:= I else Imin:= I; end until (Up + E > Ut) and (Up − E < Ut);end; Решение логарифмического уравнения (1.2.03) в 20 точках при условии RD = 0,25 Ом позволит нам получить модель 2-го и 3-го участков ВАХ диода КД213А (построена светло-зелёными точками на рис. 1.2.8):
Рис. 1.2.7. Двухполюсник, состоящий из идеального полупроводникового диода и резистора.
Наш идеальный диод VD1 при температуре 20 градусов Цельсия имеет следующее уравнение ВАХ прямого тока (см. выше):
Ln(Ia) = K • Ua + B = 29,8 • Ua − 18,7 (1.2.02).
Запишем уравнение ВАХ прямого тока нашего двухполюсника:
Ua = UD1 + Ur,
где UD1 — напряжение, падающие на идеальном диоде,
Ur — напряжение, падающее на резисторе.
Поскольку
UD1 = (Ln(Ia) − B)/K,
Ur = RD • Ia,
отсюда находим:
Ua = (Ln(Ia) − B) / K + RD • Ia,
Ia = exp(Ua • K - K • RD • Ia + B) (1.2.03)
Получить математическую модель ВАХ двухполюсника можно, решая логарифмическое уравнение (1.2.03) методом подбора. На языке Delphi оно решается при помощи следующей процедуры двоичного поиска:
procedure MidI(Ut, K, B, R: real; var I: real);var Imax, Imin, Up, E: real;begin E:= 0.00001; Imax:= exp(Ut * K + B); Imin:= 0; repeat begin I:= (Imax + Imin) / 2; Up:= I * R + (ln(I) − B) / K; if Up > Ut then Imax:= I else Imin:= I; end until (Up + E > Ut) and (Up − E < Ut);end; Решение логарифмического уравнения (1.2.03) в 20 точках при условии RD = 0,25 Ом позволит нам получить модель 2-го и 3-го участков ВАХ диода КД213А (построена светло-зелёными точками на рис. 1.2.8):
 Рис. 1.2.8. Математическая модель 2-го и 3-го участков ВАХ прямого тока кремниевого диода КД213А в полулогарифмическом масштабе.
1.2.5. Зависимость ВАХ прямого тока диода от температуры согласно уравнения Шокли.
Построим ВАХ при изменении температуры согласно уравнению Шокли. Для прямого тока PN-перехода уравнение Шокли имеет вид:
Iа = Is • exp((β • e • Uа) / (k • T))
Если выразить его как:
Iа = exp(K • Uа + B),
тогда:
K = (β • e) / (k • T) = β • 39.57065 при T = 293,
B = Ln(Is).
Для диода КД213А найдено:
β = 0,753
K =29,8
B = −18,7
Параметр B не должен влиять на наклон прямой. В современных моделях этот параметр вдруг становиться температурно-зависимым, что неверно - он не должен влиять на наклон прямой, иначе он становится зависимым и от Uа, температура в уравнении Шокли определена только в знаменателе выражения (β • e) / (k • T). Построим графики по формуле Шокли для температур 10, 20 и 30 градусов по Цельсию для диода КД213А, считая параметр В на заданном участке температур неизменным и равным −18,7. На рис. 1.2.9. по формуле Шокли построены графики для температур -20, 20 и 60 градусов по Цельсию для диода КД213А (график для температур -20 градусов Цельсия показан синими точками, 20 градусов — зелёным, 60 градусов — красным). Графики построены поверх ВАХ экспериментальных данных для диода КД213А при 20 град. Цельсия (синие точки):
Рис. 1.2.8. Математическая модель 2-го и 3-го участков ВАХ прямого тока кремниевого диода КД213А в полулогарифмическом масштабе.
1.2.5. Зависимость ВАХ прямого тока диода от температуры согласно уравнения Шокли.
Построим ВАХ при изменении температуры согласно уравнению Шокли. Для прямого тока PN-перехода уравнение Шокли имеет вид:
Iа = Is • exp((β • e • Uа) / (k • T))
Если выразить его как:
Iа = exp(K • Uа + B),
тогда:
K = (β • e) / (k • T) = β • 39.57065 при T = 293,
B = Ln(Is).
Для диода КД213А найдено:
β = 0,753
K =29,8
B = −18,7
Параметр B не должен влиять на наклон прямой. В современных моделях этот параметр вдруг становиться температурно-зависимым, что неверно - он не должен влиять на наклон прямой, иначе он становится зависимым и от Uа, температура в уравнении Шокли определена только в знаменателе выражения (β • e) / (k • T). Построим графики по формуле Шокли для температур 10, 20 и 30 градусов по Цельсию для диода КД213А, считая параметр В на заданном участке температур неизменным и равным −18,7. На рис. 1.2.9. по формуле Шокли построены графики для температур -20, 20 и 60 градусов по Цельсию для диода КД213А (график для температур -20 градусов Цельсия показан синими точками, 20 градусов — зелёным, 60 градусов — красным). Графики построены поверх ВАХ экспериментальных данных для диода КД213А при 20 град. Цельсия (синие точки):
 Рис. 1.2.9. Зависимость ВАХ от температуры согласно уравнения Шокли (графики построены поверх экспериментальных данных в полулогарифмическом масштабе).
Изучая зависимость ВАХ прямого тока от температуры согласно уравнения Шокли, можно сделать выводы:
Рис. 1.2.9. Зависимость ВАХ от температуры согласно уравнения Шокли (графики построены поверх экспериментальных данных в полулогарифмическом масштабе).
Изучая зависимость ВАХ прямого тока от температуры согласно уравнения Шокли, можно сделать выводы:
 Рис. 1.2.10. Смещение ВАХ диода при нагревании, наблюдаемое при физическом эксперименте (стрелкой указано направление смещения).
На рис. 1.2.11 приведены графики ВАХ диода КД 213А, построенных по формуле Шокли для температуры 10 градусов по Цельсию (выполнен синим цветом) и температуры 60 градусов по Цельсию (выполнен красным цветом). Стрелкой указано направление смещения ВАХ при нагревании, которое не соответствует реальности (при наблюдении физического эксперимента):
Рис. 1.2.10. Смещение ВАХ диода при нагревании, наблюдаемое при физическом эксперименте (стрелкой указано направление смещения).
На рис. 1.2.11 приведены графики ВАХ диода КД 213А, построенных по формуле Шокли для температуры 10 градусов по Цельсию (выполнен синим цветом) и температуры 60 градусов по Цельсию (выполнен красным цветом). Стрелкой указано направление смещения ВАХ при нагревании, которое не соответствует реальности (при наблюдении физического эксперимента):
 Рис. 1.2.11. Смещение ВАХ прямого тока диода при нагревании, соответствующее уравнению Шокли.
Из приведённых наблюдений можно сделать вывод, что уравнение Шокли для ВАХ прямого тока полупроводникового диода неверно.
1.2.6. Зависимость ВАХ прямого тока от температуры, наблюдаемая в эксперименте, и расчёт математической модели.
Исследуем ВАХ прямого тока при изменении температуры. Для этого измерим ВАХ прямого тока кремниевого диода КД213А при температурах 10, 20, 30, 40, 50, 60 градусов Цельсия. На рис. 1.2.12 построим графики экспериментальных данных в полулогарифмическом масштабе. Точки ВАХ имеют цвет:
Рис. 1.2.11. Смещение ВАХ прямого тока диода при нагревании, соответствующее уравнению Шокли.
Из приведённых наблюдений можно сделать вывод, что уравнение Шокли для ВАХ прямого тока полупроводникового диода неверно.
1.2.6. Зависимость ВАХ прямого тока от температуры, наблюдаемая в эксперименте, и расчёт математической модели.
Исследуем ВАХ прямого тока при изменении температуры. Для этого измерим ВАХ прямого тока кремниевого диода КД213А при температурах 10, 20, 30, 40, 50, 60 градусов Цельсия. На рис. 1.2.12 построим графики экспериментальных данных в полулогарифмическом масштабе. Точки ВАХ имеют цвет:
 Рис. 1.2.12. Экспериментальные зависимости ВАХ от температуры для диода КД213А (графики построены в полулогарифмическом масштабе).
Рис. 1.2.12. Экспериментальные зависимости ВАХ от температуры для диода КД213А (графики построены в полулогарифмическом масштабе).
 Рис. 1.2.13. Экспериментальные зависимости ВАХ от температуры для диода КД213А (графики построены в полулогарифмическом масштабе). На графике отмечены 3 характерные области участков ВАХ.
Посмотрим на ВАХ на 2-м участке (см. рис. 1.2.13.):
Рис. 1.2.13. Экспериментальные зависимости ВАХ от температуры для диода КД213А (графики построены в полулогарифмическом масштабе). На графике отмечены 3 характерные области участков ВАХ.
Посмотрим на ВАХ на 2-м участке (см. рис. 1.2.13.):
 Рис. 1.2.14. То же, что и на рисунке 1.2.13, но в другом масштабе.
Изменение температуры вызывает изменение параметров K2 и B2 прямых. Проведя расчеты для диода КД213А, получим следующие коэффициенты математической модели на 2-м участке ВАХ:
KT = 0,0956 Вольт-1•Кельвин-1,
TF = 605,2 Kельвин,
UF = 1,161 Вольт,
UB = 0,885 Вольт.
Рис. 1.2.14. То же, что и на рисунке 1.2.13, но в другом масштабе.
Изменение температуры вызывает изменение параметров K2 и B2 прямых. Проведя расчеты для диода КД213А, получим следующие коэффициенты математической модели на 2-м участке ВАХ:
KT = 0,0956 Вольт-1•Кельвин-1,
TF = 605,2 Kельвин,
UF = 1,161 Вольт,
UB = 0,885 Вольт.
 Рис. 1.2.15. Иллюстрация совпадения пучка прямых по новой формуле (1.2.07) и 2-го участка экспериментальных данных для диода КД213А.
На рис. 1.2.15 показаны графики новой математической модели ВАХ диода КД213А:
Ln(Ia/1А) = KT • (T • (UF − Ua) + TF • (Ua − UB)) (1.2.07);
где KT = 0,0956 Вольт-1•Кельвин-1,
TF = 605,2 Kельвин,
UB = 0,885 Вольт,
UF = 1,161 Вольт,
Она почти в точности соответствует сужающемуся пучку прямых (на рис. 1.2.15 видно совпадение модели - серые точки - с экспериментальными данными на 2-м участке ВАХ).
Объединив методы моделирования на 2-м и 3-м участке (см. главу 1.2.4) с учётом температурного воздействия, получим улучшенную математическую модель. Расчёты выполнялись на ЭВМ в системе программирования Delphi с применением процедуры двоичного поиска MidI. Добавочный резистор RD диода КД213А имеет величину RD=0,25 Ом:
Рис. 1.2.15. Иллюстрация совпадения пучка прямых по новой формуле (1.2.07) и 2-го участка экспериментальных данных для диода КД213А.
На рис. 1.2.15 показаны графики новой математической модели ВАХ диода КД213А:
Ln(Ia/1А) = KT • (T • (UF − Ua) + TF • (Ua − UB)) (1.2.07);
где KT = 0,0956 Вольт-1•Кельвин-1,
TF = 605,2 Kельвин,
UB = 0,885 Вольт,
UF = 1,161 Вольт,
Она почти в точности соответствует сужающемуся пучку прямых (на рис. 1.2.15 видно совпадение модели - серые точки - с экспериментальными данными на 2-м участке ВАХ).
Объединив методы моделирования на 2-м и 3-м участке (см. главу 1.2.4) с учётом температурного воздействия, получим улучшенную математическую модель. Расчёты выполнялись на ЭВМ в системе программирования Delphi с применением процедуры двоичного поиска MidI. Добавочный резистор RD диода КД213А имеет величину RD=0,25 Ом:
 Рис. 1.2.16. Иллюстрация совпадения мат. модели, построенной по формулам (1.1.8.,04), (1.1.6.,02), для 2-го и 3-го участков и экспериментальных данных ВАХ прямого тока диода КД213А (графики построены в полулогарифмическом масштабе).
На рис. 1.2.16. график математической модели построен серыми точками поверх точек экспериментальных данных. Цвет точек экспериментальных данных:
Рис. 1.2.16. Иллюстрация совпадения мат. модели, построенной по формулам (1.1.8.,04), (1.1.6.,02), для 2-го и 3-го участков и экспериментальных данных ВАХ прямого тока диода КД213А (графики построены в полулогарифмическом масштабе).
На рис. 1.2.16. график математической модели построен серыми точками поверх точек экспериментальных данных. Цвет точек экспериментальных данных:



