Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формула Ейлера для визначення критичної сили стиснутого стрижняСодержание книги
Поиск на нашем сайте
Припустимо, що під дією сили
Рис. 2. До визначення критичної сили стиснутого стрижня Віднесемо скривлену вісь стрижня до прямокутної системи координат, вибравши початок координат у точці Припустимо, що критична сила
Тут У розрахунок приймається найменша твердість стрижня На відміну від поперечного вигину при поздовжньому в правій частині цього рівняння варто ставити знак «мінус», так як абсолютна величина згинального моменту
а знак прогину завжди протилежний знаку другій похідній, тобто знаки моменту Підставивши в рівняння (3) вираз (4) для згинального моменту, одержимо
або
Увівши позначення
перепишемо рівняння (6) так:
Ми одержали однорідне лінійне диференціальне рівняння, загальний інтеграл якого, як відомо, представляється гармонійною функцією
Постійні інтегрування
З першої граничної умови виходить, що
Із другої умови одержуємо
Якщо допустити, що
Це рішення відповідає однієї з можливих форм рівноваги стиснутого стрижня, а саме — прямолінійній формі. Нас же цікавить значення сили
Корінь цього рівняння
де Однак перший корінь
Тоді з рівняння (14.7) одержимо вираз для стискаючої сили:
Рівняння (13) являє собою формулу, уперше отриману Ейлером. Практично нас цікавить найменше значення поздовжньої стискаючої сили, при якому стає можливим поздовжній згин. Найменше значення критичної сили
Вертаючись до рівнянь (10) і (12), одержимо рівняння вигнутої осі стрижня при малих деформаціях:
Найбільший прогин стрижня
Графік цієї залежності показано на рис. 3. Максимум
Рис. 3. Пружна лінія стиснутого стрижня Найменше значення аргументу, при якому косинус дорівнює нулю, буде
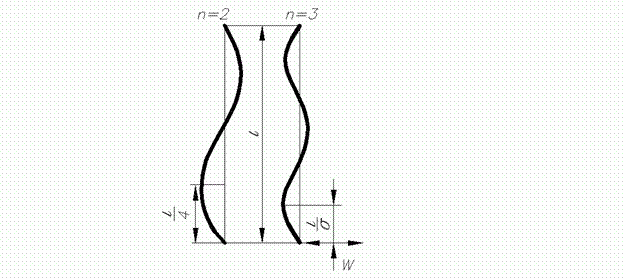
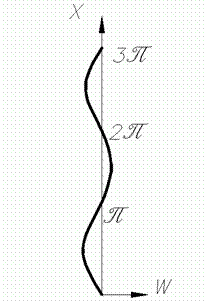
Якщо Зі співвідношення (16) або з рівняння (15) і рис. 4 виходить, що
Рис. 4. Різне число напівхвиль синусоїди
|
|||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 167; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.006 с.) |
||||||||||||||||||||||||||||||||||||||||||

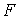 , величина якого трохи перевищує критичну силу
, величина якого трохи перевищує критичну силу 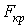 , стрижень із шарнірно закріпленими кінцями (рис. 2,а) злегка зігнувся (рис. 2,б).
, стрижень із шарнірно закріпленими кінцями (рис. 2,а) злегка зігнувся (рис. 2,б).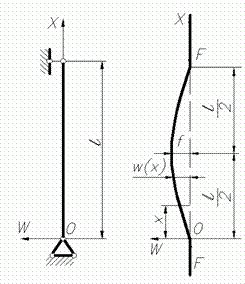
 .
. .
.
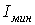 — найменший момент інерції перетину стрижня.
— найменший момент інерції перетину стрижня.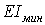 , так як очевидно, що прогин відбудеться перпендикулярно до осі найменшої жорсткості, якщо решта умов для згину у всіх площинах однакові, як у розглянутому випадку.
, так як очевидно, що прогин відбудеться перпендикулярно до осі найменшої жорсткості, якщо решта умов для згину у всіх площинах однакові, як у розглянутому випадку.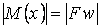 ,
,
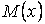 й другої похідної
й другої похідної 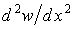 протилежні при будь-якому напрямку
протилежні при будь-якому напрямку 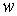 .
.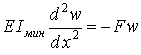 ,
,
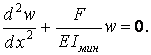
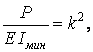
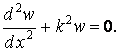
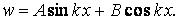
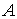 й
й 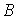 повинні бути підібрані так, щоб задовольняти граничним умовам
повинні бути підібрані так, щоб задовольняти граничним умовам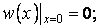
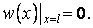
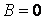 , тобто
, тобто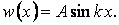
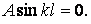
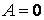 , то прогин буде тотожно дорівнювати нулю, тобто
, то прогин буде тотожно дорівнювати нулю, тобто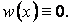
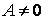 , те при скривленій формі стрижня повинне виконуватися рівність
, те при скривленій формі стрижня повинне виконуватися рівність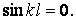
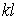 може мати нескінченна безліч значень:
може мати нескінченна безліч значень: 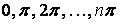 , тобто
, тобто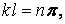
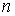 — довільне ціле число.
— довільне ціле число.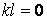 відпадає, тому що він не відповідає вихідним даним задачі. Таким чином,
відпадає, тому що він не відповідає вихідним даним задачі. Таким чином,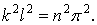

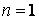 й
й  :
: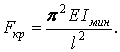
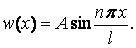
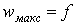 при
при 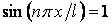 . Тоді
. Тоді 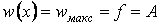 . Отже, рівняння пружної лінії стислого стрижня має вигляд
. Отже, рівняння пружної лінії стислого стрижня має вигляд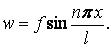
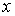 , для якого
, для якого 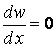 , тобто
, тобто 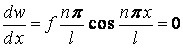 , або
, або 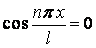 .
.
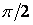 , виходить
, виходить 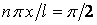 , звідки
, звідки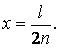
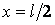 , а максимум
, а максимум