
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Головні осі й головні моменти інерціїСодержание книги
Поиск на нашем сайте
Осі, щодо яких відцентровий момент інерції дорівнює нулю, називаються головними осями (іноді їх називають головними осями інерції). Через будь-яку точку, узяту в площині перетину, можна провести в загальному випадку дві головних осі (у деяких окремих випадках їх може бути незліченна безліч). Для того щоб переконатися в справедливості цього твердження, розглянемо, як змінюється відцентровий момент інерції при повороті осей на 90° (рис.2.9).
Рис.5. До визначення положення головних осей Для довільної площадки
У процесі повороту осей, мабуть, відцентровий момент інерції змінюється безупинно, і, отже, при деякому положенні осей він стає рівним нулю. Ці осі і є головними. Головні осі можна провести через будь-яку точку перетину, але практичний інтерес представляють тільки ті з них, які проходять через центр ваги перетину; вони називаються головними центральними осями. У загальному випадку перетину довільної форми для визначення положення головних центральних осей необхідно провести спеціальне дослідження. Зараз обмежимося розглядом досить важливих окремих випадків перетинів, що мають, щонайменше, одну вісь симетрії (рис.6).
Рис.6. Головні центральні осі при наявності симетрії Проведемо через центр ваги перетину вісь
де Очевидно,
тому що для будь-якої елементарної площадки, розташованої праворуч від осі симетрії, є відповідна їй розташована ліворуч, для якої добуток координат відрізняється лише знаком. Таким чином, відцентровий момент інерції щодо осей Наведений доказ залишається в силі, якщо вісь, перпендикулярна осі симетрії, проходить і не через центр ваги перетину, тобто вісь симетрії й кожна їй перпендикулярна утворять систему головних осей. Осьові моменти інерції щодо головних центральних осей називаються головними центральними (або скорочено головними) моментами інерції.Щодо однієї з головних осей момент інерції максимальний, щодо іншої — мінімальний. Наприклад, для перетину, зображеного на рис.6, максимальним є момент інерції Таким чином, та обставина, що один з головних моментів інерції максимальний, а інший мінімальний, можна розглядати як пояснення того, що вони (і відповідні осі) називаються головними. Рівність же нулю відцентрового моменту інерції щодо головних осей - зручна ознака для їхнього знаходження. Деякі типи перетинів, наприклад, коло, квадрат, правильний шестикутник і ін. (рис.7), мають незліченну безліч головних центральних осей. Для цих перетинів будь-яка центральна вісь є головною.
Рис.7. Перетини з незліченною безліччю головних центральних осей Не приводячи доказу, укажемо, що у випадку, якщо два головних центральних моменти інерції перетину рівні між собою, то в цього перетину будь-яка центральна вісь головна й всі головні центральні моменти інерції однакові.
|
|||||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 135; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.49.243 (0.008 с.) |

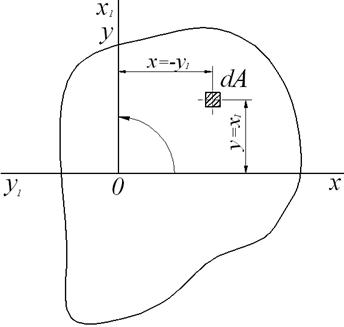
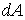 , узятої в першому квадранті системи осей
, узятої в першому квадранті системи осей 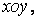 обидві координати, а, отже, і їхній добуток, додатній. У новій системі координат, поверненої щодо первісної на 90°, добуток координат розглянутої площадки від'ємний. Абсолютна величина цього добутку не змінюється, тобто
обидві координати, а, отже, і їхній добуток, додатній. У новій системі координат, поверненої щодо первісної на 90°, добуток координат розглянутої площадки від'ємний. Абсолютна величина цього добутку не змінюється, тобто 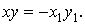 Очевидно, те ж має місце й для будь-якої іншої елементарної площадки. Значить і знак суми
Очевидно, те ж має місце й для будь-якої іншої елементарної площадки. Значить і знак суми 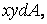 який уявляє собою відцентровий момент інерції перетину, при повороті осей на 90° змінюється на протилежний, тобто
який уявляє собою відцентровий момент інерції перетину, при повороті осей на 90° змінюється на протилежний, тобто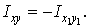
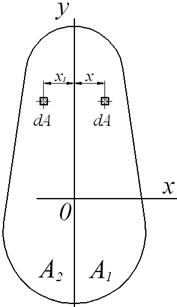
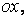 перпендикулярну осі симетрії
перпендикулярну осі симетрії 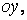 й визначимо відцентровий момент інерції
й визначимо відцентровий момент інерції 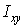 . Скористаємося відомим з курсу математики властивістю визначеного інтеграла (інтеграл суми дорівнює сумі інтегралів) і представимо
. Скористаємося відомим з курсу математики властивістю визначеного інтеграла (інтеграл суми дорівнює сумі інтегралів) і представимо 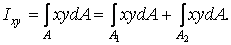
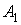 й
й 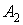 — частини площі перетину, розташовані відповідно праворуч і ліворуч від осі симетрії.
— частини площі перетину, розташовані відповідно праворуч і ліворуч від осі симетрії.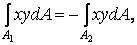
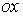 і
і 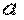 виявився рівним нулю, тобто це головні осі. Отже, для знаходження головних осей симетричного перетину досить знайти положення його центра ваги. Однієї з головних центральних осей є вісь симетрії, друга - їй перпендикулярна.
виявився рівним нулю, тобто це головні осі. Отже, для знаходження головних осей симетричного перетину досить знайти положення його центра ваги. Однієї з головних центральних осей є вісь симетрії, друга - їй перпендикулярна.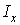 . Звичайно, говорячи про екстремальність головних моментів інерції, мається на увазі лише їхнє порівняння з іншими моментами інерції, обчисленими щодо осей, що проходять через ту ж точку перетину.
. Звичайно, говорячи про екстремальність головних моментів інерції, мається на увазі лише їхнє порівняння з іншими моментами інерції, обчисленими щодо осей, що проходять через ту ж точку перетину.



