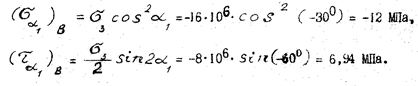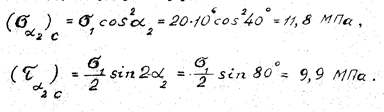Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Аналіз напруженого стану при одновісьовому розтязі. Максимальні дотичні напруження.Содержание книги
Поиск на нашем сайте
Лінійний напружений стан має місце в точках стержня, який розтягують або стискують поздовжньою силою. Розглянемо стержень призматичної форми з площею поперечного перерізу А, навантажений - зосередженими розтягуючими силами F /рис. 4/. На достатній відстані від місця прикладання сили /відповідно до принципу Сен-Венана /виберемо точку В і проведемо через цю точку поперечний переріз. Нормальна напруга в будь-якій точці цього перерізу,в тому числі і в точці В, визначається за отриманою раніше формулою
Рис. 4. До визначення напруги в точці В при лінійному напруженому стані.
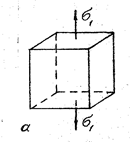
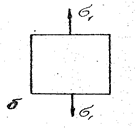
Рис. 5. Зображення лінійного напруженого стану: а – в просторі, б – на площині.
Оскільки при розтягу стержня його напружений стан однорідний, то для дослідження напруження на різних похилих площадках уявно вирізаний паралелепіпед може бути довільних розмірів, в тому числі і такий, що мав за грань поперечний переріз стержня А0. На верхній і нижній гранях паралелепіпеда паралельних площині А0, діють розтягуючі напруги, які визначаються формулою /11/. На всіх бічних гранях нормальні напруги відсутні, тому що відсутні діючі сили. Дотичні напруження на всіх гранях дорівнюють нулю, оскільки розтягуючі сили F не утворюють зсуву виділених граней паралелепіпеда. Оскільки на гранях паралелепіпеда відсутні дотичні напруги, то нормальні напруження тут будуть головними, і відповідно до формули /11/ дістанемо σ1 = у = F/A0, σ2 = 0, σ3 = 0 тобто кожна точка виділеного паралелепіпеда перебуває в лінійному напруженому стані /рис.5 а/. Надалі елемент, що перебуває в лінійному або плоскому напруженому стані, будемо зображати перерізом паралелепіпеда у вигляді плоскої фігури /рис.5,б/. У такий спосіб зображення лінійного і плоского напружених станів можна ввести більш просте правило знаків для дотичних напружень, не пов’язане з вибором системи координат: дотичні напруження на площині додатні, якщо вони намагаються повернути розглядуваний елемент відносно довільної точки, взятої всередині елемента за ходом годинникової стрілки, і від’ємні – якщо проти годинникової стрілки. Розглянемо як розподілені напруження на площині похилого перерізу. Для цього проведемо площину, нормаль nб, до якої віссю х паралелепіпеда утворює кут α /рис. 6/ На похилій площині Аα повну напругу Рα, зумовлену силами F, можна визначати за формулою:
Оскільки площина
Рис. 6. Визначення напружень σα,τ α при лінійному напруженому стані.
де враховано, що F/A0 = σ1. Проекція повної напруги
Користуючись рівнянням /14/, можна простежити за зміною значень нормального напруження на площадках, що мають різний нахил. Так, із збільшенням кута Отже, найбільше значення нормального напруження маємо на головній площадці, де Проекція напружень
Відповідно до формули (15) найбільшу дотичне напруження виникає на площадці з sin 2α = 1, тобто для якої 2α = 90° і α = 45°. Значить, на площадці, нормаль до якої з напрямом поздовжньої осі х утворює кут 45°, дотичні напруження досягають найбільших значень
При стиску головні напруження мають значення σ1 = σ2 = 0; σ3 = -F /A0. Тоді напружений стан у точці стержня визначається, як і при розтягу, лише в них замість σ1 необхідно підставляти σ3.
Приклад 1. Визначити нормальні і дотичні напруги в точці В перерізу 1-1 і в точці С перерізу 2-2 стержня, якщо його площа поперечного перерізу Ао = 20 • 10-4 м2, α1 = 300, α2 = 40°. Стержень навантажений зовнішніми силами F1 = 40 кН і F2 = 72 кН так, як показано на рис.2.6,а.
Розв'язання. Перш за все розбиваємо стержень на ділянки і, використовуючи метод перерізів, визначимо значення поздовжніх сил N1, N2 на кожній із них: N1 = F1 - F2 = 40 – 72 = - 32 кН /стиск/. Побудуємо епюру нормальних сил /рис 7,б/. Знайдемо нормальну напругу в поперечному перерізі, що проходить через точку В:
Зазначимо, що оскільки на даній ділянці виділений елемент підлягає стиску, то в точці В маємо напругу σх = σ3. Аналогічно напруга в поперечному перерізі, що проходить через точку С, буде
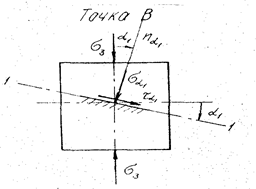
Елементи, виділені на ділянках точок В і С, головні напруги σ3 і σ1 , а також похилі площини та невідомі поки напруження на них, показані на рис.2.7, 2.8. Визначимо нормальні
Рис. 7. Епюра нормальної сили N в стержні навантаженому силами F1 і F2
Рис.8. Схема до визначання напружень
Рис. 9. Схема до визначення напруг
Відносно напряму осі х /або
Аналогічно, враховуючи знак кута α2, визначаємо напруження на похилій площині, яка утворена перерізом 2-2:
Питання для самоконтролю
1. Дати визначення лінійного, плоского і об'ємного напружених станів. Навести приклади. 2. Які правила знаків вводяться для нормальних і дотичних напруг? 3. Доведіть, що сума нормальних напруг на двох довільних взаємно перпендикулярних площадках, що проходять через дану точку навантаженого тіла, величина стала. 4. Що таке головні площини і головні напруги?
Заняття № 37 Тема: Розтяг і стиск План 1. Випробування матеріалів на розтяг. Діаграма розтягу зразків з низьковуглецевої сталі, її характеристики. 2. Характеристики пластичності. 3. Закон розвантаження і повторного навантаження. 4. Діаграми розтягу і стиску крихких і пластичних матеріалів. ЛІТЕРАТУРА основна ЛІТЕРАТУРА додаткова Студенти повинні знати: характеристики механічних властивостей матеріалів, закон навантаження, розвантаження та повторного навантаження матеріалів, значення небезпечних Студенти повинні вміти: визначати характеристики міцності та пластичності, визначати небезпечні напруження.
|
||||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 157; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.129.8 (0.01 с.) |

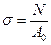 , (11)
, (11)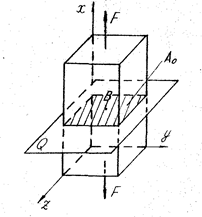
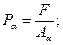 (12)
(12)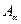 (12) зв'язана з А0 співвідношенням
(12) зв'язана з А0 співвідношенням 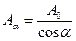 , то:
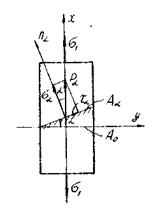
, то: 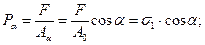 (13)
(13) 
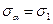 на нормаль nα утворює нормальне напруження
на нормаль nα утворює нормальне напруження 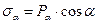 , або:
, або: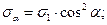 (14)
(14)  від 0 до 90° напруження σ зменшується від значення
від 0 до 90° напруження σ зменшується від значення 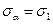
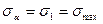 (при α=0).
(при α=0).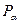 на площадку
на площадку 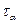 , яку можна визначити за формулою
, яку можна визначити за формулою 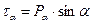 , або:
, або: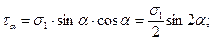 (15)
(15) 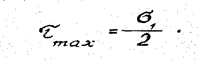 /16/
/16/
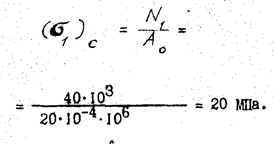
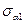 і дотичні
і дотичні 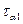 напруження на похилій площині, утвореній перерізом 1-1.
напруження на похилій площині, утвореній перерізом 1-1.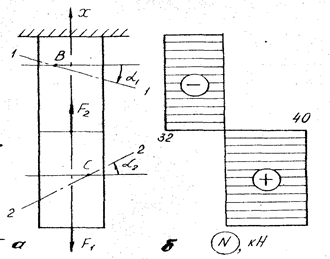
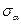 і
і 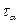 в точці В стержня, зображеного на рис.7
в точці В стержня, зображеного на рис.7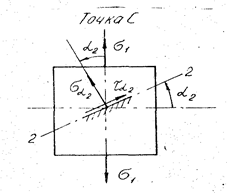
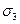 / нормаль nα, утворює кут α1, який відраховується за годинниковою стрілкою. Тому, підставляючи кут α1 в формули /14/ і /15/, його необхідно брати із знаком "мінус". Тоді за формулами /14/ і /15/
/ нормаль nα, утворює кут α1, який відраховується за годинниковою стрілкою. Тому, підставляючи кут α1 в формули /14/ і /15/, його необхідно брати із знаком "мінус". Тоді за формулами /14/ і /15/