
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Внутрішні зусилля при крученні. Крутний моментСодержание книги
Поиск на нашем сайте
Внутрішні крутні моменти в поперечних перерізах валу визначаються методом перерізів з умови рівноваги відсіченої частини вала: ΣМz = 0. Крутний момент у довільному поперечному перерізі валу дорівнює алгебраїчній сумі зовнішніх моментів, що скручують (включаючи і реакції закріплення), прикладених до нього по одну сторону від розглянутого перерізу. У найпростішому випадку, коли вал, навантажений по краях тільки двома зовнішніми моментами, що рівні один одному за величиною і зворотними з напрямком, крутний момент у будь-якому поперечному перерізі вала за величиною дорівнює цим зовнішнім моментам.
У більш складних випадках, коли до вала прикладені кілька зовнішніх моментів, крутні моменти у поперечних перерізах будуть неоднакові на різних ділянках вала. При розрахунках на міцність і жорсткість знак моменту, що крутить, не має особливого значення, однак для зручності прийняте наступне правило знаків: крутний момент, вважається додатним, якщо при погляді в торець відсіченої частини вала, зовнішній момент представляється спрямованим по годинниковій стрілці. Додатні і від’ємні напрямки моменту, що крутить, показані на рис.4. Зміну крутних моментів по довжині вала зручно представляти за допомогою епюр моментів, які будуються згідно загальнім правилам. При побудові епюр моментів варто мати на увазі, що в перерізі, у якому на вал діє зовнішній зосереджений момент, ордината епюри міняється стрибкоподібно на величину, рівну значенню цього моменту.
Рис. 4 Якщо прямий вал знаходиться у стані спокою чи рівномірного обертання, то алгебраїчна сума всіх зовнішніх моментів, прикладених до нього дорівнює нулю. При розрахунку валів у ряді випадків величини зовнішніх моментів, що скручують, визначають за величиною споживаної потужності і по швидкості обертання вала. Якщо вал робить за хвилину n оборотів, то кут повороту вала за 1 секунду, виражений у радіанах, дорівнює
Робота моменту, що скручує, Мскр за 1 сек, тобто потужність Р, що передається валом, дорівнює добутку величини моменту, що скручує, на кут повороту вала в радіанах за секунду:
Звідси, якщо потужність виражена в кН·м, знаходимо:
Розглянемо методику побудови епюр крутних моментів на прикладі. Нехай вал АВ /рис.5,а/ обертається рівномірно. Тоді алгебраїчна сума крутильних моментів, прикладених до шківів, дорівнює нулю: Т1 + Т2 + Т3 + Т4 = 0. Розбиваємо вал на силові ділянки: І, ІІ, ІІІ, ІV, V. Межами кожної з них є перерізи, на яких розміщені шківи, а також початок і кінець вала. Оскільки тертям в підшипниках нехтуємо, то в довільному перерізі на ділянках І і V крутний момент дорівнює нулю, тобто Мк1 = 0, МкV=0.
Рис.5. Епюра крутних моментів навантаженого вала
Проведемо довільний поперечний переріз на ділянці ІІ вала в межах 0 ≤
Рис.6. Схема до визначення величини крутного момента в перерізі через крутильні моменти /ліва відрізана частина вала/
Користуючись визначенням крутного момента на другій ділянці, можна сформулювати такий порядок визначення Мк в поперечних перерізах вала.
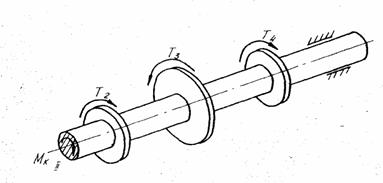
Рис.7. Схема до визначення величини крутного момента в перерізі через крутильні моменти /права відрізана частина вала/
1. Площиною, перпендикулярною до осі вала, розтинають його в потрібному перерізі. 2. Записують крутний момент у перерізі як алгебраїчну суму крутильних моментів, розміщених по один із боків перерізу. В цьому разі в рівняння для Мк крутильний момент Т записують із знаком "плюс", якщо, дивлячись на переріз, він повертає відсічену частину вала проти годинникової стрілки, із знаком "мінус"- якщо за годинниковою стрілкою. Провівши довільні розтини на інших силових ділянках вала, отримаємо відповідно:
Значення крутних моментів на різних ділянках вала зручно зображати в вигляді епюри, тобто графіка, що показує, як змінюється крутний момент під час переходу від перерізу до перерізy вздовж вала. Під час побудови епюр крутних моментів користуються загальними правилами побудови епюр.
На рис.5,б зображена епюра крутних моментів вала, що показаний на рис.5,а. Аналізуючи побудовану епюру, звертаємо увагу на те, що до вала прикладено крутильний момент Т3 = 400 Нм, найбільший крутий момент в перерізах вала на перевищує 200 Нм. Саме цю величину, а не Т3 = 400 Нм необхідно використати в розрахунках на міцність і короткість вала.
Запитання для самоконтролю
1. Який вид деформації називається крученням? Яка величина в кількісною характеристикою деформації кручення? 2. Сформулюйте правило знаків для крутного момента Мк. 3. Як визначається напруга в поперечному перерізі вала при крученні? Який характер її розподілу по площі поперечного перерізу?
Заняття № 48 Тема: Кручення План 1. Кручення прямого бруса круглого перерізу. Основні гіпотези. Напруження в поперечному перерізі брусу. Кут закручення. Полярні моменти інерції для круга та кільця. Момент опору.
Студент повинен знати: Закон Гука. Внутрішні силові фіктори при крученні. Визначення дотичних напружень. Визначення кутів закручування, умову міцності та жорсткості при крученні. Студент повинен вміти: визначати напруження та кути закручування при деформації. ЛІТЕРАТУРА ОСНОВНА [ 2 ] §§ 4,1 - 4,2; [12] §§ 4.2 ЛІТЕРАТУРА ДОДАТКОВА 1. Кручення прямого бруса круглого перерізу. Основні гіпотези. Напруження в поперечному перерізі брусу. Кут закручення. Полярні моменти інерції для круга та кільця. Момент опору. Кручення – це один з простих видів навантаження (деформування) бруса, при якому у поперечному перерізі бруса діє тільки внутрішній крутний момент ( Розглянемо задачу кручення круглого вала (рис. 8) з геометричної, статичної та фізичної сторін. Теоретичні і експериментальні дослідження деформації кручення круглого вала дають підстави прийняти таку геометричну модель (рис. 8 а): 1 Вісь вала при крученні залишається прямолінійною. 2 Поперечні перерізи вала, плоскі до деформації, залишаються в своїй площині і лише повертаються навколо осі вала. Таким чином, відстані між поперечними перерізами вала у процесі деформації не змінюються. 3 Радіуси перерізу залишаються при крученні прямолінійними.
Рис. 8 – Модель кручення круглого вала Кручення у відповідності з цією моделлю подається як результат зсувів, визначених взаємним обертанням перерізів. Кут закручення
Рівняння (5) встановлює закон зростання кутових деформацій Розглянемо статичну сторону задачі. Зробимо переріз на довільній відстані
У цьому рівнянні шуканою величиною є закон розподілу дотичних напружень Фізична сторона задачі представлена законом Гука при зсуві
З розв’язувальної системи рівнянь (5) – (7) після підстановки (5) у (7), а потім у (6) маємо:
звідкіля отримає розрахункову формулу для погонного кута закручення: де добуток Повний кут закручення
Якщо вал має декілька ділянок, що відрізняються розмірами перерізів і значенням крутного моменту, то повний кут закручення дорівнює алгебраїчній сумі кутів закручення окремих ділянок. Після підстановки (9) у (5), а потім у (7) отримаємо загальну формулу дотичних напружень у довільній точці перерізу закручуваного вала: Таким чином, дотичні напруження при крученні зростають за лінійним законом пропорційно відстані точки перерізу від осі вала, згідно з епюрою Максимальні напруження діють у найвіддаленіших від осі точках перерізу, при
де Умова міцності при крученні
де При необхідності перевіряють також умову жорсткості вала
де В цих формулах внутрішній крутний момент Питання для самоконтролю 1. Запишіть умову міцності при крученні. Які три типи задач вона дозволяє розв'язувати? 2. Що таке жорсткість перерізу при крученні? 3. Напишіть формулу для визначення відносного і повного кута закручування. 4. Поясніть, чому вал кільцевого перерізу при крученні економічніший за вал суцільного перерізу. 5. Порядок розрахунку вала на міцність і жорсткість. 6. Як обчислити величину осідання циліндричної гвинтової пружини при стиску? 7. Як зміняться дотичні напруги в пружині /за інших однакових величин/, якщо діаметр дроту збільшити /зменшити/ удачі?
Заняття № 49 Тема: Кручення. План 1. Три види розрахунків на міцність та жорсткість. Студент повинен знати: сутність розрахунків на міцність та жорсткість, основні формули. Студент повинен вміти: визначати напруження та кути закручування при деформації, а таж проводити проектні та перевірочні розрахунки на міцність і жорсткість при деформації кручення.
ЛІТЕРАТУРА ОСНОВНА ЛІТЕРАТУРА ДОДАТКОВА
Розрахунки на міцність при крученні
Із умови міцності витікають три види розрахунків на міцність:
1. Перевірочний розрахунок При розрахунку на жорсткість по заданих навантаженнях і геометричних характеристиках вала визначаються найбільші дотичні напруження і порівнюється з допустимими. При цьому найбільші дотичні напруження визначаються в небезпечному перерізі, в якому крутний момент найбільший по абсолютній величині. Для визначення небезпечного перерізу зручно будувати епюру крутних моментів.
де
Проектний розрахунок Для проведення проектного розрахунку перш за все з умови міцності /13/ визначають полярний момент опору:
Потім, враховуючи формули для визначення осьового моменту опору поперечного перерізу, знаходять діаметри: А) для вала суцільного круглого перерізу:
Б) для вала кільцевого поперечного перерізу:
|
||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 343; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.253.199 (0.011 с.) |

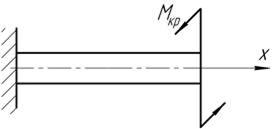 Рис. 3
Рис. 3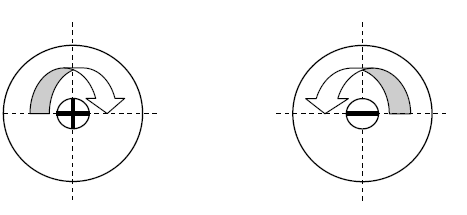
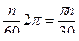
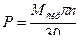
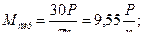 (кНм)
(кНм)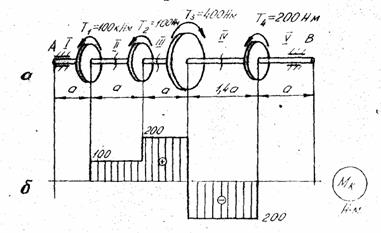
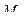 ≤ а. Частина вала зліва від перерізу /рис.6/ буде розміщена в рівновазі під дією крутильного момента Т1 і крутного момента в перерізі
≤ а. Частина вала зліва від перерізу /рис.6/ буде розміщена в рівновазі під дією крутильного момента Т1 і крутного момента в перерізі 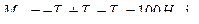 , тобто такий же, як і зліва.
, тобто такий же, як і зліва.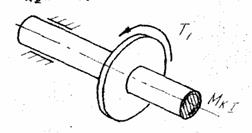
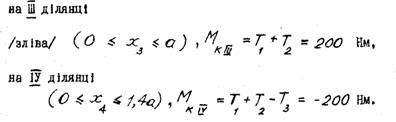
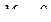 ). Брус, навантажений крутним моментом, називають валом (незалежно від форми перерізу).
). Брус, навантажений крутним моментом, називають валом (незалежно від форми перерізу).
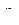 вважаємо лінійною функцією
вважаємо лінійною функцією  , тобто погонний (відносний) кут закручення
, тобто погонний (відносний) кут закручення  не змінюється по довжині вала:
не змінюється по довжині вала: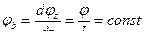 . (3)
. (3) Прямолінійна твірна
Прямолінійна твірна  (рис. 8 а), нанесена на поверхні вала, перетворюється у гвинтову лінію
(рис. 8 а), нанесена на поверхні вала, перетворюється у гвинтову лінію 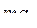 . Для неї відносний зсув (кут зсуву)
. Для неї відносний зсув (кут зсуву)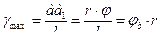 . (4)
. (4)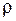 , то твірна
, то твірна 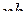 на його поверхні перетворюється у гвинтову лінію
на його поверхні перетворюється у гвинтову лінію 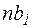 . При закрученні на той же кут
. При закрученні на той же кут 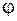 дуга
дуга 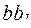 менша, ніж дуга
менша, ніж дуга  , тому і відносний зсув буде меншим:
, тому і відносний зсув буде меншим: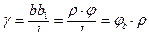 . (5)
. (5)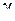 пропорційно відстані
пропорційно відстані 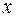 від затиснення (рис. 8 а). При зсуві в поперечних перерізах вала виникають тільки дотичні напруження. Виділимо на перерізі (рис. 5, б) нескінченно малу площадку
від затиснення (рис. 8 а). При зсуві в поперечних перерізах вала виникають тільки дотичні напруження. Виділимо на перерізі (рис. 5, б) нескінченно малу площадку 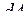 на відстані
на відстані 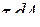 , яка діє на цій площадці, створює відносно осі вала елементарний момент
, яка діє на цій площадці, створює відносно осі вала елементарний момент  . Повний момент внутрішніх сил (внутрішній крутний момент)
. Повний момент внутрішніх сил (внутрішній крутний момент)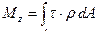 . (6)
. (6)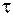 , а момент
, а момент 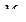 вважаємо вже визначеним за зовнішніми навантаженнями з умов рівноваги відрізаної частини вала.
вважаємо вже визначеним за зовнішніми навантаженнями з умов рівноваги відрізаної частини вала.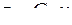 . (7)
. (7)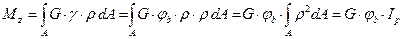 , (8)
, (8)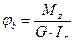 , (9)
, (9)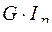 називається жорсткістю при крученні.
називається жорсткістю при крученні. (10)
(10)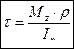 (11)
(11)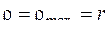 :
: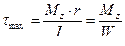 , (12)
, (12)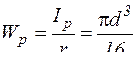 – полярний момент опору.
– полярний момент опору.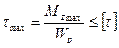 , (13)
, (13)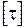 – допустиме напруження при крученні;
– допустиме напруження при крученні; 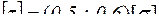 .
.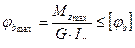 , (14)
, (14)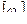 – допустимий погонний кут закручення.
– допустимий погонний кут закручення.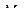 у довільному перерізі дорівнює алгебраїчній сумі зовнішніх крутних моментів, розташованих з однієї сторони від перерізу.
у довільному перерізі дорівнює алгебраїчній сумі зовнішніх крутних моментів, розташованих з однієї сторони від перерізу.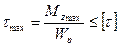
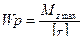 ; (15)
; (15) (16)
(16)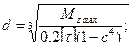 Де
Де 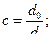 (17)
(17)


