
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритм восстановления u по V или V по U.
Поскольку действительная и мнимая части взаимосвязаны условиями Коши-Римана, то достаточно одной её части, чтобы восстановить вторую часть, а далее всю функцию Например, нам известна
Итак, алгоритм: 1. Проверить выполнение уравнения Лапласа (иначе 2. Вычислить криволинейный интеграл. 3. В полученной функции Задача 30. Дано Решение. Сначала проверяем уравнение Лапласа.
Итак, найдём криволинейный интеграл
Если известно, что Ответ.
Задача 31. Дано Решение. Сначала проверим уравнение Лапласа
Их сумма равна 0. Уравнение Лапласа выполняется. Поэтому данная
При этом, если дано Итак, Получить вид Ответ.
Практика 4 (неделя с 21 по 27 сентября). Задача 32. А. Найти Решение. Проверим уравнение Лапласа.
Сумма вторых производных равна 0. Ищем При произвольном выборе начальной точки,
Итак,
Для сравнения - старым методом:
Ответ.
|
|||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 98; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.96.224 (0.013 с.) |
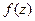 .
.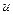 . Тогда
. Тогда 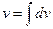 =
= 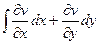 , это криволинейный интеграл 2 рода для векторного поля
, это криволинейный интеграл 2 рода для векторного поля 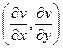 от фиксированной точки, например (0,0) до произвольной
от фиксированной точки, например (0,0) до произвольной 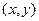 . Нам неизвестны эти частные производные, как и сама функция
. Нам неизвестны эти частные производные, как и сама функция 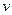 , однако их можно заменить на известные, по условиям Коши-Римана.
, однако их можно заменить на известные, по условиям Коши-Римана.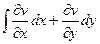 =
= 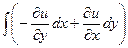 и далее вычислить.
и далее вычислить.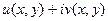 выразить
выразить 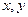 по формулам:
по формулам: 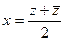 ,
, 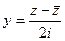 . При правильном вычислении сократятся все
. При правильном вычислении сократятся все 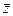 и останется только
и останется только 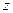 .
.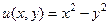 . Найти мнимую часть и восстановить вид функции
. Найти мнимую часть и восстановить вид функции 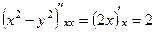 ,
, 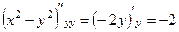 , сумма 2-й производных равна 0, то есть
, сумма 2-й производных равна 0, то есть 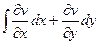 =
= 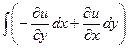 , где
, где 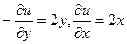 .
.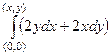 . Сделаем это с помощью интегрирования по ломаной, как при вычислении потенциала поля.
. Сделаем это с помощью интегрирования по ломаной, как при вычислении потенциала поля.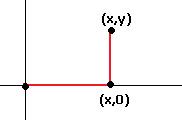
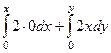 =
= 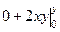 =
= 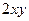 .
.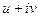 =
= 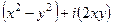 , то далее найти вид
, то далее найти вид 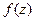 - делали в задаче 29,
- делали в задаче 29, 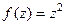
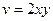 .
. 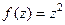
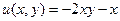 ,
, 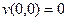 . Найти
. Найти 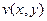 .
.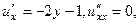
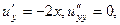 в сумме 0.
в сумме 0.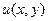 может являться одной из компонент какой-либо комплексной функции. Далее надо вычислить
может являться одной из компонент какой-либо комплексной функции. Далее надо вычислить 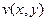 , найдём её в виде потенциала от её градиента:
, найдём её в виде потенциала от её градиента: 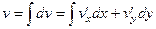 то есть в виде потенциала векторного поля
то есть в виде потенциала векторного поля 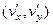 . Дело в том, что в такой записи можно заменить производные от неизвестной функции
. Дело в том, что в такой записи можно заменить производные от неизвестной функции 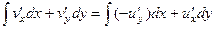 . А первые производные от
. А первые производные от 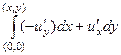 =
= 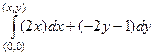 =
= 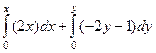 =
=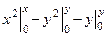 =
= 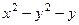 , а так как начальная точка (0,0) была взята произвольно, могла быть и иная точка, то надо записать с точностью до константы:
, а так как начальная точка (0,0) была взята произвольно, могла быть и иная точка, то надо записать с точностью до константы: 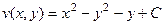 .
.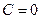 .
.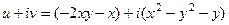 .
. 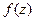 - см. задачу 28:
- см. задачу 28: 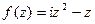 .
. 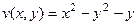 .
. 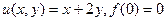 .
.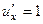
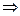
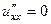 ,
, 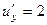
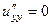 .
.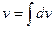 =
= 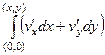 =
= 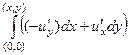 =
= 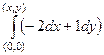 =
= 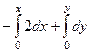 =
= 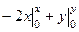 =
= 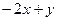 .
.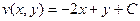 , из условия
, из условия 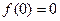 определим константу
определим константу 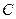 . Если
. Если 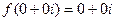 то
то 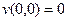 , тогда
, тогда 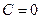 .
.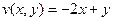 .
.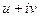 =
= 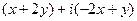 =
= 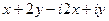 =
= 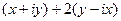 . Здесь можно даже не пользоваться формулами
. Здесь можно даже не пользоваться формулами 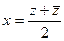 ,
, 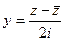 , ведь мы уже сумели получить
, ведь мы уже сумели получить 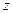 в первой скобке, а во 2-й
в первой скобке, а во 2-й 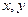 в обратном порядке и одна с минусом, если домножить и поделить на
в обратном порядке и одна с минусом, если домножить и поделить на 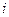 , то также удастся получить выражение с
, то также удастся получить выражение с 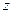 .
. =
= 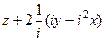 =
= 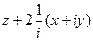 =
= 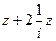 =
= 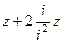 =
= 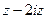 .
. 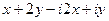 =
= 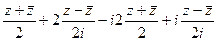 =
=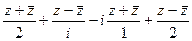 =
= 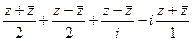 =
=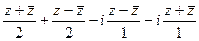 =
= 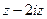 .
. 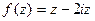 .
.


