
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Практика 1 (неделя до 6 сентября).Стр 1 из 7Следующая ⇒
Приходовский М.А. Математика - 3 семестр Курс практических занятий Учебное пособие Группы 519-1-2, 529, 539. Томск ТУСУР 2020 Оглавление по темам
Оглавление по номерам практик Практика № 1...................................................... 3 Практика № 2........................................................11 Практика № 3........................................................20 Практика № 4........................................................28 Практика № 5........................................................35 Практика № 6........................................................42 Практика № 7........................................................48 Практика № 8........................................................54 Практика № 9........................................................
Практика 1 (неделя до 6 сентября). Комплексные числа Задача 1. Умножить и поделить в алгебраической форме числа Решение. Умножим эти числа.
Поделим, с помощью умножения на сопряжённое:
Ответ. Задача 2. Умножить и поделить Решение.
Ответ. Задача 3. Разделить 1) с помощью умножения на сопряжённое число 2) в тригонометрической форме. 3) в показательной форме. Решение. 1) 2) Построим чертёж, найдём модуль и аргумент каждого из 2 чисел.
Модули ищутся по теореме Пифагора и равны Аргументы: Итак, Делим их модули и вычитаем аргументы.
3) Ответ.
Задача 4. Умножить 1) с помощью обычного раскрытия скобок. 2) в тригонометрической форме. 3) в показательной форме. Решение. 1) 2) Построим чертёж и найдём тригонометрическую форму каждого из чисел.
Умножаются их модули и складываются аргументы.
3) Ответ.
Задача 5. Вычислить в показательной форме Решение.
Для 1-го числа: Тогда Ответ. Дом. задание. Задачу 5 можно самостоятельно решить без показательной формы, умножением на сопряжённое. Задача 6. Возвести в степень: Решение. Перейдём к показательной форме, для этого сначала найдём модуль и аргумент числа
Чертёж, показывающий, расположение
Ответ. Задача 7. Возвести в степень в показательной форме: Решение. Сначала построим чертёж и найдём
По чертежу видно, что угол здесь на 45 град. меньше чем 180, то есть 135 градусов, то есть
Ответ
Задача 8. Возвести в степень Решение. Аналогично прошлой задаче, сначала переводим в показательную форму. Угол здесь 30 градусов, то есть
Тогда Теперь можем отнять полный оборот
Домашняя задача. Как в задаче 8, возвести в степень Задача 9. Вычислить Решение. Представим каждое число в показательной форме.
Задача 10. Вычислить Решение. Представим в показательной форме каждое из чисел.
Ответ.
Домашняя задача. Вычислить Корни из комплексных чисел. Вспомнить формулу: Задача 11. Вычислить Решение. Для числа По формуле
Ответ.
Задача 12. Вычислить Решение. Сначала запишем число в тригонометрической форме.
Ответ.
Задача 13. Вычислить Решение. Формула: Сначала найдём модуль и аргумент исходного числа.
Тогда
Чертёж:
Ответ. Условия Коши-Римана. В следующей серии задач надо представить функцию в виде
Задача 21. Решение. Заметим, что условия Коши-Римана не выполнены, даже 1-е:
Ответ. Задача 22. Функцию Решение.
Поэтому Заметим, что здесь нарушено уже даже 1-е условие Коши-Римана:
Ответ.
Задача 23. Решение. Раскроем скобки и перегруппируем слагаемые, чтобы сначала шли именно те, в которых нет мнимой единицы
Условия Коши-Римана не выполняются, даже 1-е из них:
Ответ.
Задача 24. Решение. Далее по формуле Эйлера
Проверим выполнение условий Коши-Римана.
Они совпадают (1-е условие Коши-Римана).
Они противоположны (2-е условие Коши-Римана). Ответ. Задача 25. Решение. Домножили на сопряжённое, чтобы в знаменателе получилось некое единое действительное число, а разбиение на Re и Im осталось только в числителе. Тогда дробь можно будет разбить на сумму или разность двух дробей.
- внутри
Проверим условия Коши-Римана
Первое условие выполнено.
Ответ.
Задача 26. Решение. Если
далее раскроем по формуле Эйлера: ... = воспользуемся чётностью косинуса и нечётностью синуса: ... =
тогда Это можно ещё записать в таком виде, используя гиперболические синус и косинус: Проверим условия Коши-Римана.
Первое условие выполнено.
Ответ.
Задача 27. Решение.
Проверим условия Коши-Римана.
Условия Коши-Римана выполнены. Ответ.
Обратная задача: Восстановление функции Примечание. С помощью формул Задача 28. Дано: Решение. Вспомним, что: и применим эти выражения в записи
= =
Ответ.
Задача 29. Дано: Решение. Подставим
Ответ.
Интегральная формула Коши. Следующая серия задач решается с помощью формул Коши:
Задача 41 (из лекц.). Вычислить Решение. Окружность радиуса 1,5. Следовательно, точка разрыва 1 внутри, а точка
Ответ. Задача 42. Вычислить Решение. Здесь, в отличие от прошлого примера, уже не 2 а 3-я степень.
Ответ. Пример 43. Доказать Решение. Здесь по обобщённой интегральной формуле Коши при любом n получается, что нужно рассматривать
Далее будут комбинированные задачи, состоящие из нескольких подзадач, где контур проводится сначала вокруг той или иной точки разрыва, а затем вокруг всех этих точек. Задача 44. Вычислить А) Решение. В знаменателе разложим на множители, и станет видно, что корни многочлена там 2 и
Если контур радиуса 0,5 окружает одну из точек, то надо применить интегральную формулу Коши, где точка
А) Б) В) В третьем пункте, где контур окружает уже обе точки, достаточно будет воспользоваться теоремой Коши и суммировать результаты двух предыдущих пунктов. Получится Ответы. А) Задача 45. Вычислить А) Решение. В каждом случае применяем интегральную формулу Коши к той или иной точке разрыва функции, 2, 3 и 5. Убирая соответствующий множитель из знаменателя, затем подставляем в оставшуюся часть функции это число. А) Б) В) Если радиус 6, то все 3 точки находятся внутри контура. Суммируем все 3 результата: Г) В последнем случае, лишь две из трёх точек внутри контура: Д) Ответы. А)
Задача 46. Вычислить Решение.
Ответ. 0. Задача 47. Вычислить А) Решение.
|
|||||||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 101; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.8.42 (0.257 с.) |
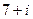 и
и 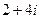 .
.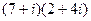 =
= 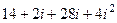 =
=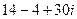 =
= 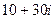 .
.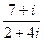 =
= 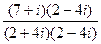 =
= 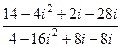 =
= 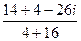 =
= 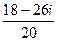 =
= 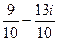 =
= 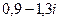 .
.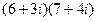 .
.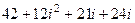 =
= 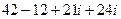 =
= 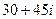 .
.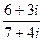 =
= 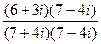 =
= 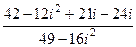 =
= 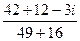 =
= 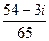 .
.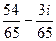 .
. 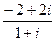 тремя способами:
тремя способами: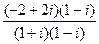 =
= 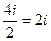 .
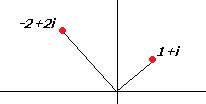
.
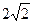 и
и 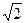 .
.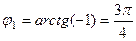 ,
, 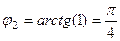 .
.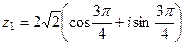
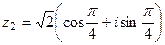 .
.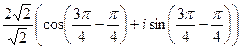 =
=  =
=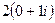 =
= 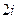 .
. 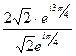 =
= 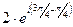 =
= 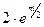 =
= 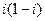 тремя способами:
тремя способами: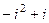 =
= 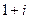 .
.
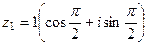
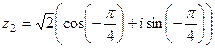 .
.
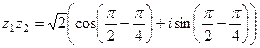 =
= 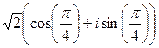 =
=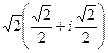 =
= 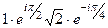 =
= 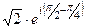 =
= 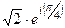 , а далее раскроем по формуле Эйлера
, а далее раскроем по формуле Эйлера 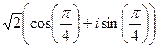 =
= 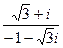 .
.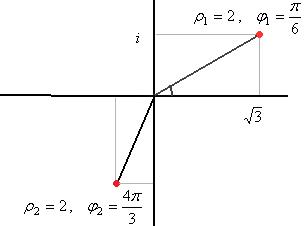
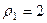 ,
, 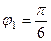 . Для 2-го:
. Для 2-го: 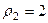 ,
, 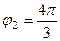 .
. 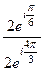 =
= 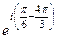 =
= 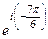 =
= 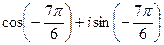 , прибавим
, прибавим 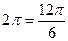 , для удобства вычисления. Итак,
, для удобства вычисления. Итак, 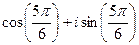 =
= 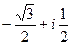 .
.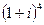 .
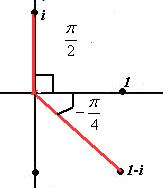
.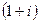 с помощью чертежа. Число в 1-й четверти, угол 45 градусов.
с помощью чертежа. Число в 1-й четверти, угол 45 градусов.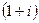 на плоскости, это число выделено красным цветом:
на плоскости, это число выделено красным цветом: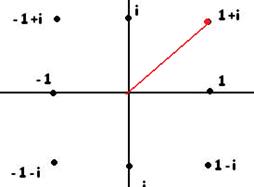
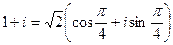 =
= 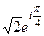 . По формуле Муавра,
. По формуле Муавра, 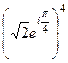 =
=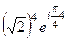 =
= 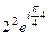 =
= 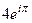 =
= 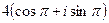 =
= 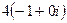 =
= 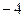 .
. 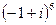 .
.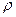 и
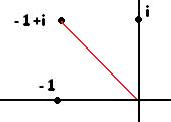
и 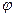 .
.
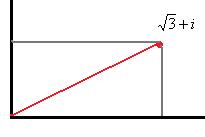
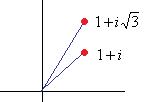
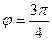 , Проекции красной линии на координатные оси имеют длину 1 (каждая), поэтому
, Проекции красной линии на координатные оси имеют длину 1 (каждая), поэтому 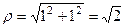 . Тогда
. Тогда 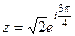 ,
, 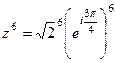 =
=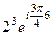 =
= 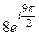 =
= 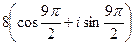 , мы можем отбросить 1 или более полных оборотов, при этом синус и косинус не изменятся, то есть отнять
, мы можем отбросить 1 или более полных оборотов, при этом синус и косинус не изменятся, то есть отнять 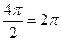 , либо
, либо 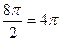 . Тогда угол
. Тогда угол 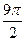 эквивалентен
эквивалентен 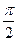 , и остаётся вычислить:
, и остаётся вычислить: 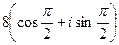 =
= 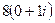 =
= 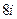 .
.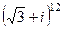 .
. 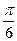 , модуль
, модуль 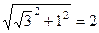 . Итак,
. Итак, 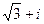 =
= 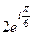 .
.
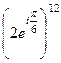 =
= 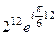 =
= 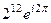 =
= 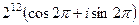
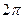 , косинус и синус при этом не меняются. тогда получим
, косинус и синус при этом не меняются. тогда получим 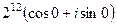 =
= 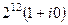 =
= 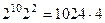 =
= 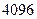 . Ответ.
. Ответ. 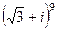 . Ответ.
. Ответ. 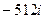
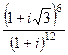
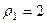 ,
, 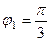 ,
, 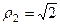 ,
, 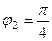 .
.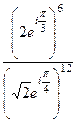 =
= 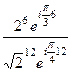 =
= 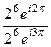 =
= 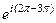 =
= 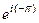 =
= 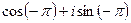 но можно произвольно прибавить
но можно произвольно прибавить 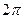 , ведь от этого не изменятся синус и косинус, поэтому
, ведь от этого не изменятся синус и косинус, поэтому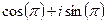 =
= 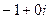 =
= 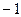 . Ответ.
. Ответ. 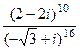 .
. 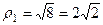 ,
, 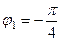 и
и 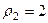 ,
, 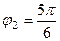 . Тогда
. Тогда =
= 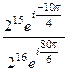 =
= 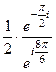 здесь в числителе прибавили угол
здесь в числителе прибавили угол 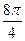 , кратный
, кратный 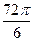 . Далее,
. Далее, 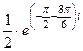 =
= 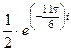 =
= 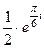 =
= 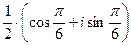 =
= 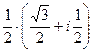 =
= 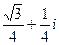 .
.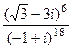 . Ответ.
. Ответ. 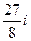
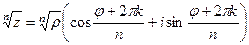 .
.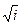 .
.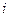 :
: 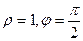 .
.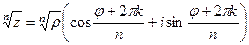 получаем
получаем 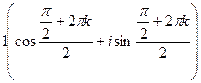 =
= 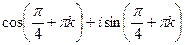 , значений будет всего 2.
, значений будет всего 2.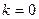 :
: 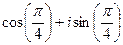 =
= 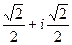 ,
,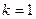 :
: 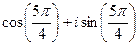 =
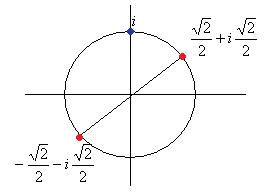
= 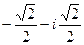 .
.
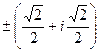
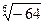 .
.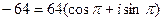 . Тогда
. Тогда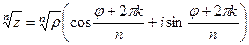
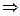
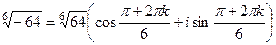 =
=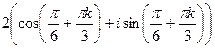 . Начертим окружность радиуса 2 и отметим там 6 точек, первой соответствует угол 300, остальные больше на 600, 1200 и так далее.
. Начертим окружность радиуса 2 и отметим там 6 точек, первой соответствует угол 300, остальные больше на 600, 1200 и так далее. 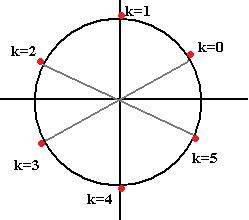
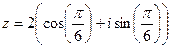
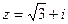
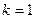
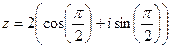
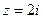
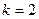
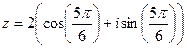
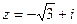
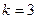
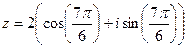
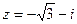
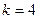
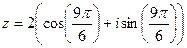

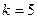
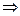
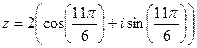
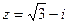 .
.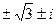 и
и 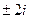 .
.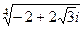
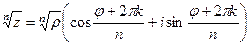 .
.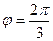 (т.к. 90 градусов и ещё 30 во второй четверти),
(т.к. 90 градусов и ещё 30 во второй четверти),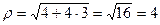 .
.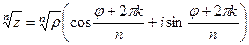 =
= 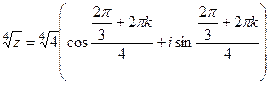 =
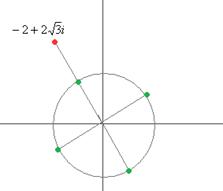
= 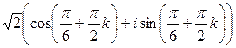 таким образом, 4 точки лежат на окружности, углы 300, 1200, 2100, 3000 (по +900 добавить 4 раза). Отмечены на чертеже зелёным. Здесь 4 корня:
таким образом, 4 точки лежат на окружности, углы 300, 1200, 2100, 3000 (по +900 добавить 4 раза). Отмечены на чертеже зелёным. Здесь 4 корня: :
: 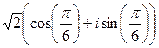 =
= 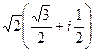 =
= 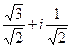 .
. 
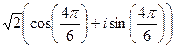 =
= 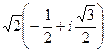 =
= 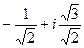 .
. 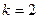 :
: 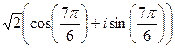 =
= 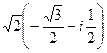 =
= 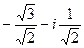 .
. 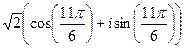 =
= 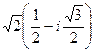 =
=  .
. 
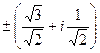 и
и 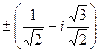 .
.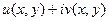 , а также проверить выполнение условий Коши-Римана.
, а также проверить выполнение условий Коши-Римана.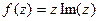 представить в виде
представить в виде 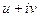 , и проверить выполнение условий Коши-Римана.
, и проверить выполнение условий Коши-Римана. 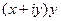 =
= 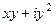
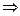
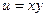 ,
, 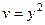 .
.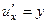 ,
, 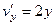 не равны между собой.
не равны между собой.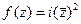 представить в виде
представить в виде  =
= 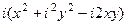 =
=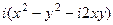 =
= 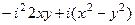 =
= 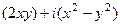 .
.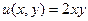 ,
, 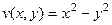 .
.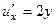 ,
, 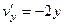 .
.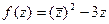 представить в виде
представить в виде 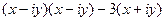
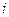 , а затем те, в которых она есть.
, а затем те, в которых она есть.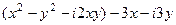 =
= 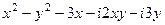 =
=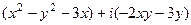
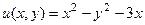 .
. 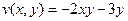 .
.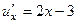 .
. 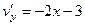 , они противоположны, а должны совпадать.
, они противоположны, а должны совпадать.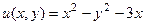 .
. 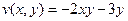 .
.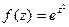 представить в виде
представить в виде 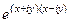 =
= 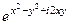 =
= 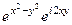
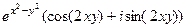 =
=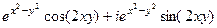 .
.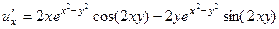
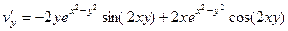
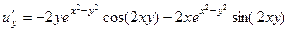
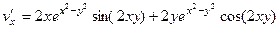
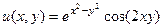 ,
, 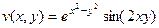 .
.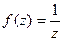 представить в виде
представить в виде 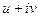 , проверить условия Коши-Римана.
, проверить условия Коши-Римана.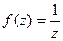 =
= 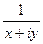 =
= 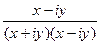
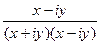 =
= 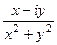 =
= 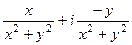 ,
,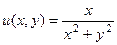 ,
, 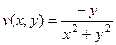 .
. 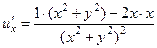 =
= 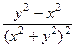
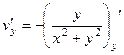 =
= 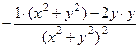 =
= 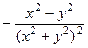 =
= 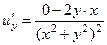 ,
, 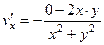 =
= 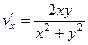 , они противоположны, второе условие выполнено.
, они противоположны, второе условие выполнено.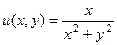 ,
, 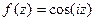 представить в виде
представить в виде 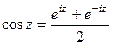 , то
, то 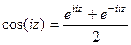 =
=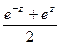 =
= 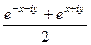 =
= 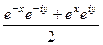
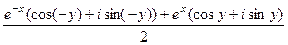 =
=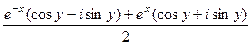 =
=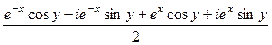 =
=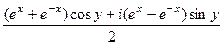 =
= 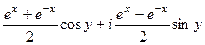 ,
,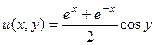 ,
, 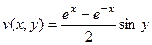 .
.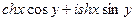 .
.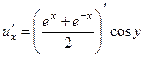 =
= 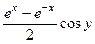
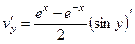 =
= 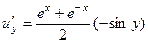
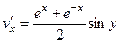 , они противоположны, второе условие выполнено.
, они противоположны, второе условие выполнено.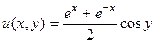 ,
, 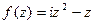 представить в виде
представить в виде 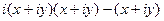 =
=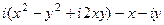 =
= 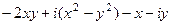 =
= 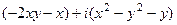 , тогда
, тогда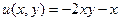 ,
, 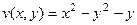 .
.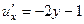
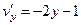 совпадают;
совпадают; 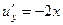
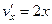 противоположные.
противоположные. 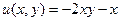 ,
, 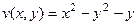 .
.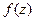 по разложению
по разложению 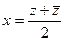 ,
, 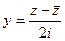 .
.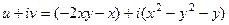 . Восстановить функцию
. Восстановить функцию 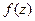 . (обратная к задаче 27).
. (обратная к задаче 27).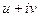 .
.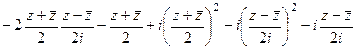 =
=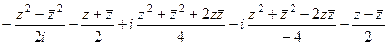 =
= =
=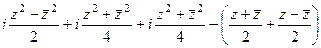 =
=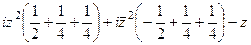 =
= 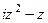
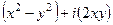 . Найти вид
. Найти вид 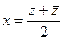 ,
, 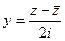 .
.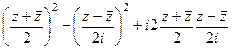 =
= 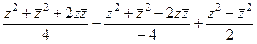 =
=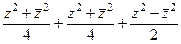 =
= 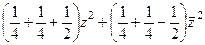 =
= 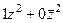 =
= 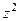 . Итак,
. Итак, 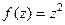 .
.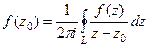 и
и 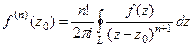 .
.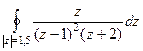 .
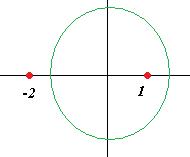
.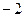 снаружи, поэтому для неё считать не надо. Однако упустить множитель
снаружи, поэтому для неё считать не надо. Однако упустить множитель 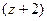 при записи нельзя, ведь в функции он остаётся.
при записи нельзя, ведь в функции он остаётся. 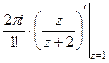 =
= 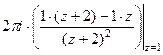 =
= 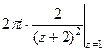 =
= 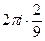 =
= 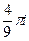 .
.
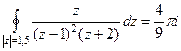 .
.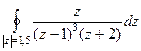 .
.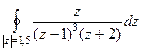 =
= 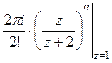 =
= 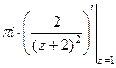 =
=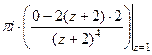 =
= 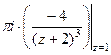 =
= 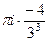 =
= 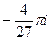 .
.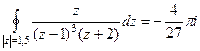 .
.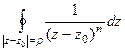 = 0 для целого
= 0 для целого 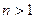 .
.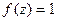 . Но ведь любая производная от константы 1 есть 0. Поэтому результат 0.
. Но ведь любая производная от константы 1 есть 0. Поэтому результат 0.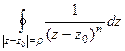 = 0 для
= 0 для 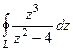 , где контур
, где контур 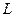 :
: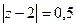 Б)
Б) 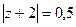 В)
В) 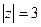 .
.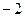 .
.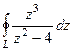 =
= 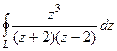 .
.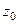 одна из них, а именно, в первом пункте
одна из них, а именно, в первом пункте 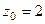 , а во втором
, а во втором 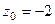 . Надо убрать из знаменателя соответствующую скобку, и присвоить конкретное
. Надо убрать из знаменателя соответствующую скобку, и присвоить конкретное 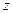 в оставшейся части функции.
в оставшейся части функции. 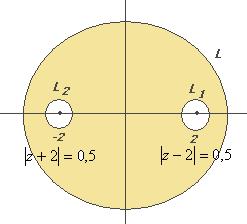
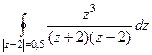 =
= 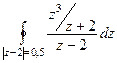 =
= 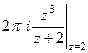 =
= 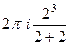 =
= 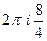 =
= 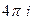 .
.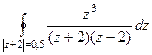 =
= 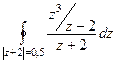 =
= 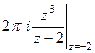 =
= 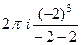 =
= 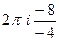 =
= 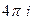 .
.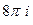 .
.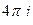 Б)
Б) 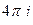 В)
В) 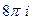 .
.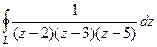 , где контур
, где контур 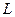 :
: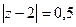 Б)
Б) 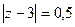 В)
В) 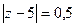 Г)
Г) 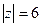 Д)
Д) 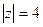 .
.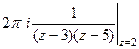 =
= 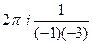 =
= 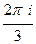 .
.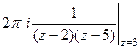 =
= 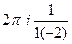 =
= 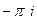 .
.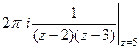 =
= 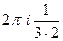 =
= 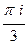 .
.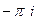 +
+ 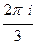
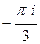 .
.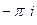 В)
В) 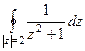 .
.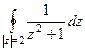 =
= 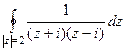 . Здесь две особые точки, это
. Здесь две особые точки, это 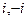 , они являются полюсами 1 порядка. Тогда в каждой из этих точек применим интегральную формулу Коши.
, они являются полюсами 1 порядка. Тогда в каждой из этих точек применим интегральную формулу Коши.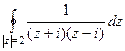 =
= 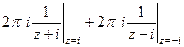 =
=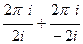 =
= 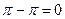 .
.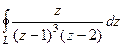 , где контур
, где контур 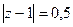 В)
В) 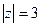 .
.


