
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Практика 6 (неделя с 5 по 11 октября).
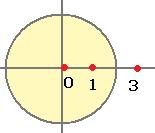
Задача 51. Вычислить Решение. Внутри окружности радиуса 2 лежат 2 из 3 особых точек, а именно, 0 и 1, точка 3 снаружи.
Поэтому интегральную формулу Коши применяем только к двум точкам.
Предварительно вычислим производную.
Далее,
Задача 52. Вычислить Решение. Ответ.
Особые точки и вычеты. Задача 53. Найти все особые точки и определить их тип для функции Решение. Здесь нужно сначала преобразовать выражение в знаменателе, выделить множители, соответствующие каждому корню.
Ответ. Полюсы 1-го порядка: Задача 54. Найти все особые точки и определить их тип для функции Решение. Разложим знаменатель на множители,
При Ответ. Полюсы 1-го порядка: Задача 55. Исследовать тип особой точки Решение. Здесь в знаменателе 3-я степень, но в этой точке в числителе тоже 0, и он влияет на итоговый порядок полюса. Надо в числителе разложить в ряд, чтобы остались одни лишь только степенные функции, потом вынесем за скобку минимальную степень, и это будет определять порядок нуля в числителе.
В числителе и знаменателе нули соответственно 1-го и 3-го порядка. После сокращения на
Ответ. Задача 56. Исследовать тип особой точки Решение. Во-первых, сразу видно, что
Ответ.
Напомним формулы вычисления вычетов (из лекций).
Она следует из формулы Коши:
Она следует из формулы Коши: Задача 57. Вычислить вычет Эквивалентная формулировка: вычислить Решение. Точка
Ответ. Замечание. По интегральной формуле Коши то же самое: Задача 58. Вычислить вычет Решение. Точка
Более конкретно эта формулы выглядит так:
Ответ. Задача 59. Вычислить вычет Решение. Несмотря на то, что видим здесь
Таким образом, Тогда
Ответ.
Задача 60. Вычислить вычеты во всех особых точках и в Решение. Особые точки здесь 1 и
Для вычисления
Ответ.
Задача 61. Вычислить вычет Решение. Здесь 7 это полюс 3-го порядка. Тогда надо использовать формулу Итак,
Задача 62. Вычислить вычет Решение. Заметим, что здесь всего одна особая точка в плоскости, это
|
|||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 93; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.236.62 (0.016 с.) |
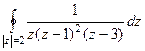 .
.
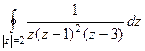 =
= 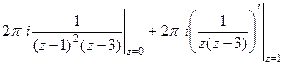 .
.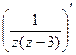 =
= 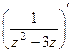 =
= 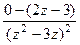 =
= 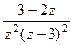 .
.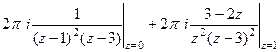 =
=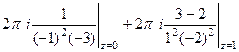 =
= 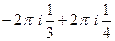 =
=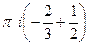 =
= 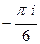 . Ответ.
. Ответ. 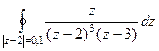 .
.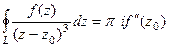 , тогда
, тогда 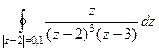 =
= 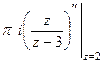 =
= 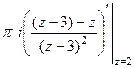 =
= 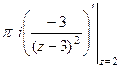 =
= 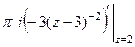 =
= 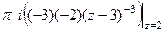 =
= 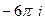
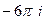 .
.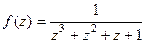 .
.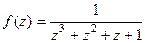 =
= 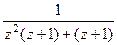 =
= 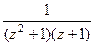 =
= 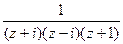 . Таким образом, полюсы 1-го порядка:
. Таким образом, полюсы 1-го порядка: 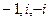 .
.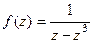 .
.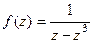 =
= 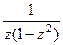 =
= 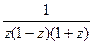 .
.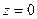 ,
, 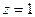 ,
, 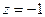 нули 1-го порядка в знаменателе, тогда для функции это полюсы 1 порядка.
нули 1-го порядка в знаменателе, тогда для функции это полюсы 1 порядка.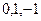 .
.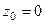 для
для 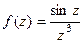 .
.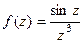 =
= 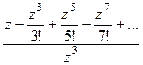 =
= 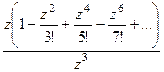
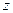 видно, что полюс 2 порядка, так как в скобках осталась функция, не стремящаяся к 0 в
видно, что полюс 2 порядка, так как в скобках осталась функция, не стремящаяся к 0 в 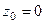 .
.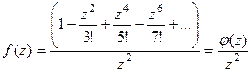 .
.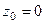 полюс 2 порядка.
полюс 2 порядка.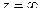 для
для 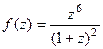 .
.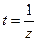 , этим самым мы получим возможность вместо
, этим самым мы получим возможность вместо 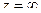 исследовать точку
исследовать точку 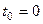 .
.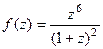
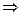
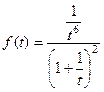 =
= 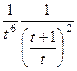 =
= 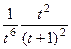 =
=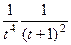 . Итак, в знаменателе осталось
. Итак, в знаменателе осталось 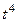 . Точка
. Точка 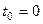 полюс 4-го порядка. Значит,
полюс 4-го порядка. Значит, 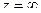 полюс 4-го порядка.
полюс 4-го порядка.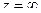 полюс 4-го порядка.
полюс 4-го порядка.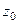 полюс порядка 1:
полюс порядка 1: 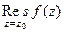 =
= 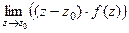 .
.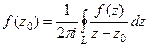
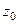 полюс порядка m:
полюс порядка m: 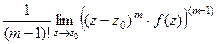 .
.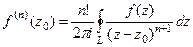 .
.
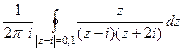 .
.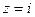 является полюсом 1-го порядка. Вычисляем по формуле
является полюсом 1-го порядка. Вычисляем по формуле 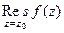 =
= 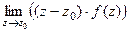 .
.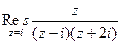 =
= 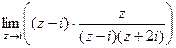 =
= 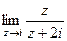 =
= 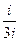 =
= 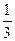 .
.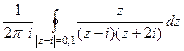 =
= 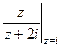 =
= 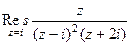
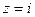 является полюсом 2-го порядка. Вычисляем по формуле
является полюсом 2-го порядка. Вычисляем по формуле 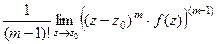 при
при 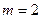 .
.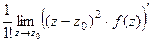 . В этом конкретном примере получается
. В этом конкретном примере получается 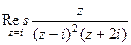 =
= 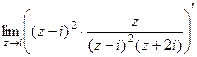 =
=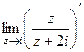 =
= 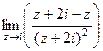 =
= 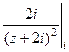 =
= 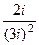 =
= 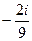 .
.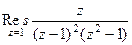
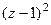 , тем не менее, полюс
, тем не менее, полюс 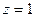 не 2-го порядка, потому что в другом множителе тоже присутствует
не 2-го порядка, потому что в другом множителе тоже присутствует 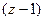 .
. 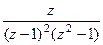 =
= 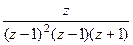 =
= 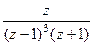 .
.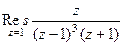 =
= 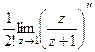 =
= 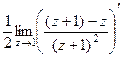 =
=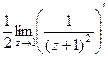 =
= 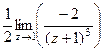 =
= 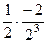 =
= 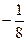 .
. для функции
для функции 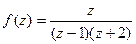 .
.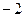 , полюсы 1 порядка.
, полюсы 1 порядка.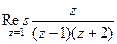 =
= 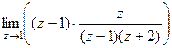 =
= 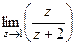 =
= 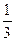 .
.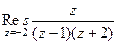 =
= 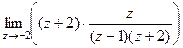 =
= 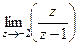 =
= 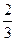 .
.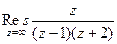 использовать тот факт, что
использовать тот факт, что 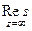 противоположен сумме всех вычетов в конечных особых точках. Тогда
противоположен сумме всех вычетов в конечных особых точках. Тогда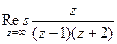 =
= 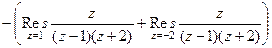 =
= 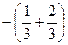 =
= 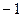 .
.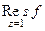 =
= 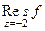 =
= 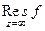 =
= 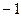 .
.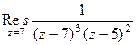 .
.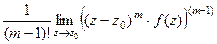 , которая при
, которая при 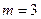 выглядит так:
выглядит так: 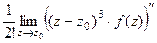 .
.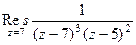 =
= 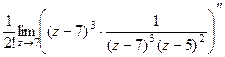 =
=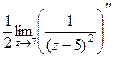 =
= 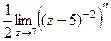 =
= 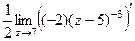 = =
= = 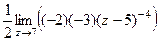 =
= 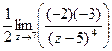 =
= 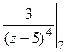 =
=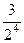 =
= 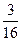 . Ответ.
. Ответ. 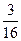 .
.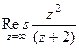 .
.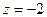 . Таким образом, вычет в
. Таким образом, вычет в  .
. 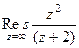 =
= 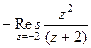 =
= 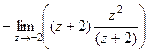 =
= 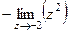 =
= 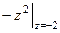 =
= 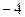 . Ответ.
. Ответ. 


