
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Способ 2. По формуле Ньютона-Лейбница.Содержание книги Поиск на нашем сайте
Заметив, что функция
Ответ. Домашняя задача. Вычислить
Задача 38. Вычислить Решение. Здесь тоже можно вычислять как без, так и по формуле Ньютона-Лейбница. Но разница в объёме вычислений будет огромная. Так как функция аналитическая, нам не важно, соединены точки по дуге окружности или по какой-то другой линии, на самом деле результат зависит только от первообразной в начальной и конечной точках. Сделаем по формуле Ньютона-Лейбница.
Ответ. Для сравнения, № 38 можно решить в качестве домашней задачи и без формулы Ньютона-Лейбница.
Задача 39. Вычислить Решение. Здесь сумма степенных функций, они являются аналитическими. Поэтому используем формулу Ньютона-Лейбница.
Отдельно вычислим
Тогда Ответ. Задача 40. Вычислить Решение. Можно применять формулу Ньютона-Лейбница, так как функция
Ответ. Домашняя задача. Вычислить Решение. Вычислим квадрат и куб этого числа.
Тогда
Практика 5 (неделя с 28 сентября по 4 октября). Интегральная формула Коши. Следующая серия задач решается с помощью формул Коши:
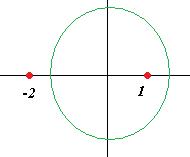
Задача 41 (из лекц.). Вычислить Решение. Окружность радиуса 1,5. Следовательно, точка разрыва 1 внутри, а точка
Ответ. Задача 42. Вычислить Решение. Здесь, в отличие от прошлого примера, уже не 2 а 3-я степень.
Ответ. Пример 43. Доказать Решение. Здесь по обобщённой интегральной формуле Коши при любом n получается, что нужно рассматривать
Далее будут комбинированные задачи, состоящие из нескольких подзадач, где контур проводится сначала вокруг той или иной точки разрыва, а затем вокруг всех этих точек. Задача 44. Вычислить А) Решение. В знаменателе разложим на множители, и станет видно, что корни многочлена там 2 и
Если контур радиуса 0,5 окружает одну из точек, то надо применить интегральную формулу Коши, где точка
А) Б) В) В третьем пункте, где контур окружает уже обе точки, достаточно будет воспользоваться теоремой Коши и суммировать результаты двух предыдущих пунктов. Получится Ответы. А) Задача 45. Вычислить А) Решение. В каждом случае применяем интегральную формулу Коши к той или иной точке разрыва функции, 2, 3 и 5. Убирая соответствующий множитель из знаменателя, затем подставляем в оставшуюся часть функции это число. А) Б) В) Если радиус 6, то все 3 точки находятся внутри контура. Суммируем все 3 результата: Г) В последнем случае, лишь две из трёх точек внутри контура: Д) Ответы. А)
Задача 46. Вычислить Решение.
Ответ. 0. Задача 47. Вычислить А) Решение. А) Б) В этом случае корень знаменателя имеет кратность 3, так что придётся считать с помощью 2-й производной. Конкретизируем обобщённую формулу Коши для 3 степени:
В) Ответы. А) Задача 48. Вычислить А) Решение. А) Б) В) 0 + Ответы. А) 0 Б)
Задача 49. Вычислить А) Решение. Так как здесь в интеграле уже изначально есть множитель А) Б) В) В отличие от двух первых точек, здесь в знаменателе корень 2-го порядка, поэтому подставляем
Г) По интегральной теореме Коши, сумма интегралов по трём предыдущим контурам: Ответы. А) Задача 50. Вычислить Решение. Здесь две особые точки,
Ответ. 0.
|
||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 133; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.136.19.203 (0.007 с.) |

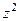 аналитическая, т.е. для неё выполняются условия Коши-Римана, можно не раскрывать скобки предыдущим способом, а вычислить первообразную по
аналитическая, т.е. для неё выполняются условия Коши-Римана, можно не раскрывать скобки предыдущим способом, а вычислить первообразную по 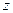 в начальной и конечной точке.
в начальной и конечной точке.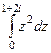 =
= 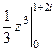 =
= 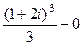 , а дальше всё сводится просто к вычислению степени комплексного числа.
, а дальше всё сводится просто к вычислению степени комплексного числа.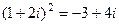
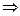
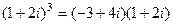 =
= 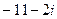 , тогда
, тогда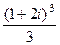 =
= 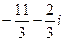 .
.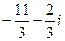
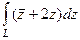 , где
, где 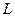 дуга параболы
дуга параболы 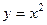 (от точки 0 до
(от точки 0 до 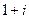 ). Ответ.
). Ответ. 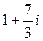 .
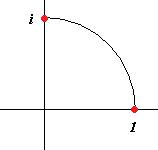
.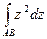 по участку единичной окружности в 1-й четверти от 1 до
по участку единичной окружности в 1-й четверти от 1 до 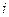 .
.
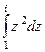 =
= 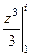 =
= 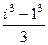 =
= 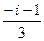 =
= 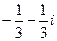 .
.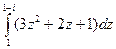 .
.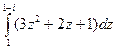 =
= 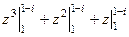 =
= 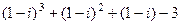 .
.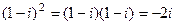 ,
,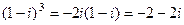 .
.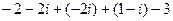 =
= 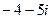 .
.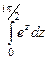 .
.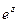 аналитическая.
аналитическая.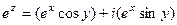 , тогда:
, тогда: 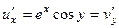 ,
, 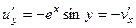 .
.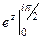 =
= 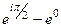 =
= 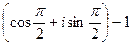 =
= 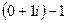 =
=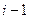 =
= 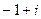 .
.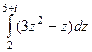 . Ответ.
. Ответ. 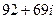 .
.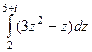 =
= 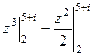 =
= 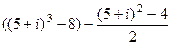 .
.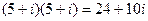 ,
,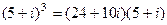 =
= 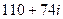 .
.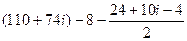 =
= 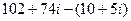 =
=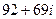 . Ответ.
. Ответ. 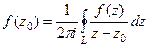 и
и 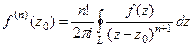 .
.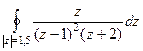 .
.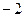 снаружи, поэтому для неё считать не надо. Однако упустить множитель
снаружи, поэтому для неё считать не надо. Однако упустить множитель 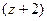 при записи нельзя, ведь в функции он остаётся.
при записи нельзя, ведь в функции он остаётся. 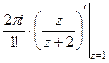 =
= 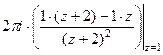 =
= 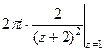 =
= 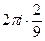 =
= 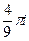 .
.
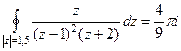 .
.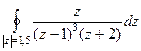 .
.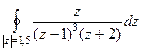 =
= 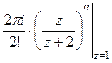 =
= 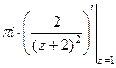 =
=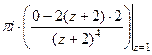 =
= 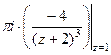 =
= 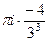 =
= 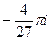 .
.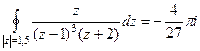 .
.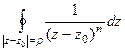 = 0 для целого
= 0 для целого 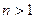 .
.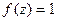 . Но ведь любая производная от константы 1 есть 0. Поэтому результат 0.
. Но ведь любая производная от константы 1 есть 0. Поэтому результат 0.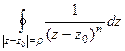 = 0 для
= 0 для 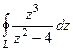 , где контур
, где контур 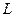 :
: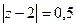 Б)
Б) 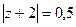 В)
В) 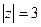 .
.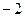 .
.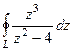 =
= 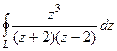 .
.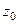 одна из них, а именно, в первом пункте
одна из них, а именно, в первом пункте 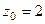 , а во втором
, а во втором 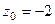 . Надо убрать из знаменателя соответствующую скобку, и присвоить конкретное
. Надо убрать из знаменателя соответствующую скобку, и присвоить конкретное 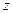 в оставшейся части функции.
в оставшейся части функции. 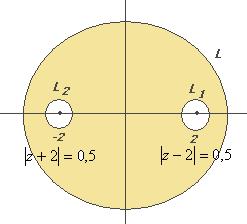
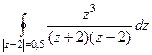 =
= 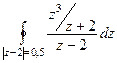 =
= 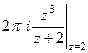 =
= 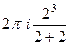 =
= 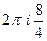 =
= 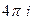 .
.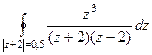 =
= 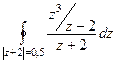 =
= 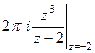 =
= 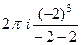 =
= 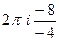 =
= 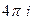 .
.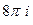 .
.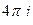 Б)
Б) 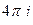 В)
В) 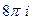 .
.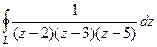 , где контур
, где контур 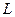 :
: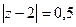 Б)
Б) 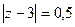 В)
В) 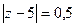 Г)
Г) 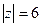 Д)
Д) 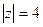 .
.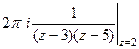 =
= 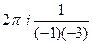 =
= 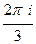 .
.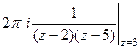 =
= 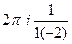 =
= 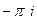 .
.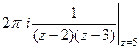 =
= 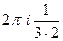 =
= 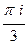 .
.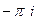 +
+ 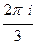
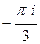 .
.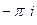 В)
В) 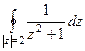 .
.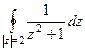 =
= 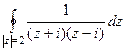 . Здесь две особые точки, это
. Здесь две особые точки, это 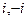 , они являются полюсами 1 порядка. Тогда в каждой из этих точек применим интегральную формулу Коши.
, они являются полюсами 1 порядка. Тогда в каждой из этих точек применим интегральную формулу Коши.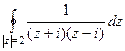 =
= 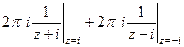 =
=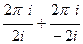 =
= 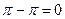 .
.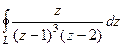 , где контур
, где контур 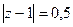 В)
В) 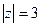 .
.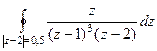 =
= 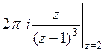 =
= 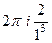 =
= 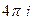 .
.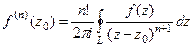 , при n=2:
, при n=2: 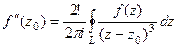 . Тогда
. Тогда 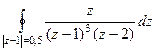 =
= 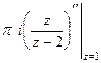 =
=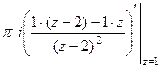 =
= 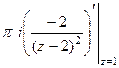 =
= 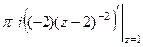 =
= 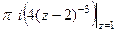 =
= 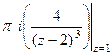 =
= 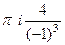 =
= 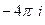 .
.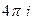 Б)
Б) 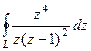 , где контур
, где контур 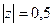 Б)
Б) 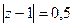 В)
В) 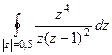 =
= 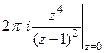 =
= 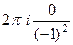 = 0.
= 0.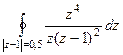 =
= 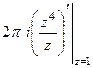 =
= 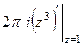 =
= 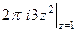 =
= 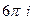 .
.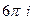 =
= 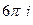 .
.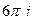 В)
В) 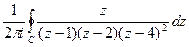 , где контур С:
, где контур С: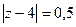 Г)
Г) 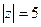 .
.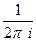 , то домножать на
, то домножать на 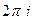 в правой части не нужно.
в правой части не нужно.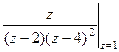 =
= 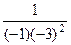 =
=  .
.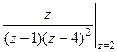 =
= 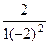 =
= 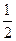 .
.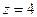 не сразу, а после вычисления производной.
не сразу, а после вычисления производной. 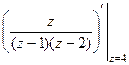 =
= 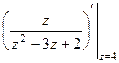 =
= 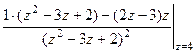 =
= 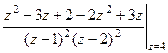 =
= 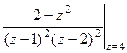 =
= 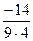 =
= 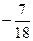 .
.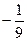 +
+ 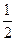
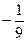 Б)
Б) 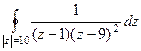 .
.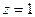 полюс 1-го порядка и
полюс 1-го порядка и 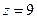 полюс 2-го порядка. Для 2-й точки надо применять обобщённую формулу Коши (с производной).
полюс 2-го порядка. Для 2-й точки надо применять обобщённую формулу Коши (с производной).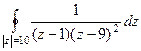 =
= 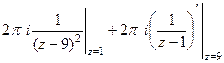 =
=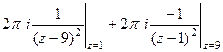 =
=  =
=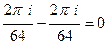 .
.


