
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача 17-А (рекомендуемое д-з).Содержание книги Поиск на нашем сайте
Дано Это действие, обратное к тому, что в задаче 17. Поэтому очевидно, что в ответе должно получиться
Задача 18. Найти все значения Решение. Используем формулу
Ответ.
Задача 19. Вычислить Решение. Применяем формулу Ответ. Заметим, что
Задача 20. Решить уравнение Решение. Введём замену
1) решим это уравнение и найдём 2) учитывая Квадратичное уравнение решаем через дискриминант, здесь Далее,
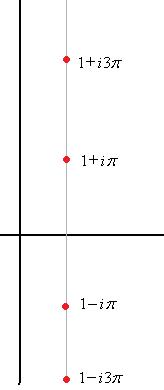
Получилось две бесконечных последовательности точек, одна выше а другая ниже действительной прямой. По горизонтали расстояние между соседними ровно Чертёж:
Замечание. Если число в правой части уменьшать до 1, то обе эти последовательности сближаются и в итоге соединятся в одну, расположенную на действительной прямой. Это будут в таком случае уже давно знакомые решения равенства Общий случай. Если
Практика 3 (неделя с 14 по 20 сентября).
Условия Коши-Римана. В следующей серии задач надо представить функцию в виде
Задача 21. Решение. Заметим, что условия Коши-Римана не выполнены, даже 1-е:
Ответ. Задача 22. Функцию Решение.
Поэтому Заметим, что здесь нарушено уже даже 1-е условие Коши-Римана:
Ответ.
Задача 23. Решение. Раскроем скобки и перегруппируем слагаемые, чтобы сначала шли именно те, в которых нет мнимой единицы
Условия Коши-Римана не выполняются, даже 1-е из них:
Ответ.
Задача 24. Решение. Далее по формуле Эйлера
Проверим выполнение условий Коши-Римана.
Они совпадают (1-е условие Коши-Римана).
Они противоположны (2-е условие Коши-Римана). Ответ. Задача 25. Решение. Домножили на сопряжённое, чтобы в знаменателе получилось некое единое действительное число, а разбиение на Re и Im осталось только в числителе. Тогда дробь можно будет разбить на сумму или разность двух дробей.
- внутри
Проверим условия Коши-Римана
Первое условие выполнено.
Ответ.
Задача 26. Решение. Если
далее раскроем по формуле Эйлера: ... = воспользуемся чётностью косинуса и нечётностью синуса: ... =
тогда Это можно ещё записать в таком виде, используя гиперболические синус и косинус: Проверим условия Коши-Римана.
Первое условие выполнено.
Ответ.
Задача 27. Решение.
Проверим условия Коши-Римана.
Условия Коши-Римана выполнены. Ответ.
Обратная задача: Восстановление функции Примечание. С помощью формул Задача 28. Дано: Решение. Вспомним, что: и применим эти выражения в записи
= =
Ответ.
Задача 29. Дано: Решение. Подставим
Ответ.
|
|||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 192; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.4.152 (0.009 с.) |

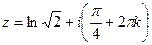 , вычислить
, вычислить 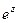 .
.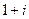
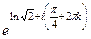 =
= 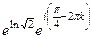 =
= 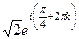 =
= 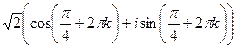 =
= 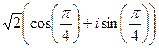 =
=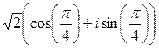 =
= 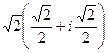 =
= 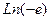 .
. 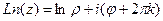 .
.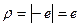 . Так как
. Так как 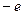 это действительное отрицательное число, то значит,
это действительное отрицательное число, то значит, 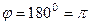 . Итак,
. Итак, 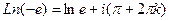 =
= 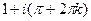 . Таким образом, это точки в комплексной плоскости, имеющие вид:
. Таким образом, это точки в комплексной плоскости, имеющие вид: 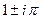 ,
, 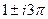 ,
, 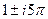 ,...
,...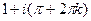 .
.
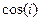 .
.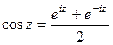 , где аргумент вместо
, где аргумент вместо 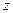 подставим
подставим 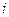 . Тогда
. Тогда 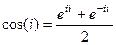 =
= 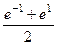 =
= 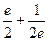 .
.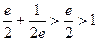 , то есть модули значений косинуса вне действительной оси не ограничены отрезком
, то есть модули значений косинуса вне действительной оси не ограничены отрезком 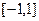 .
.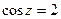 .
.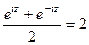
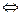
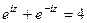
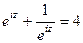 .
.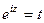 , при этом получаем
, при этом получаем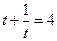
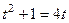
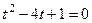 . Задача разбивается на 2 шага
. Задача разбивается на 2 шага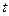 ,
,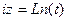 и далее найдём
и далее найдём 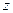 .
.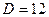 , тогда
, тогда 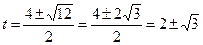 . Оба значения
. Оба значения 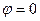 .
.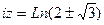
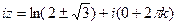
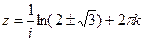 =
= 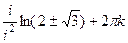 =
= 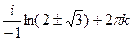 =
= 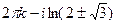 .
.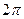 .
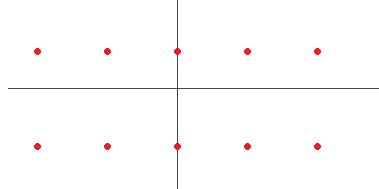
.
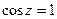 , т.е.
, т.е. 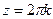 .
.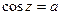 то
то 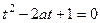 ,
, 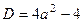 ,
, 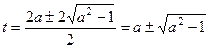 . Тогда
. Тогда 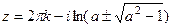 , что при
, что при 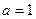 порождает
порождает 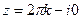 .
.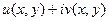 , а также проверить выполнение условий Коши-Римана.
, а также проверить выполнение условий Коши-Римана.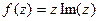 представить в виде
представить в виде 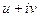 , и проверить выполнение условий Коши-Римана.
, и проверить выполнение условий Коши-Римана. 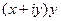 =
= 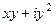
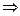
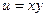 ,
, 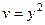 .
.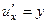 ,
, 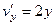 не равны между собой.
не равны между собой.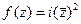 представить в виде
представить в виде  =
= 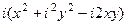 =
=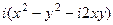 =
= 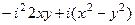 =
= 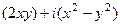 .
.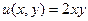 ,
, 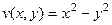 .
.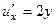 ,
, 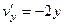 .
.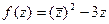 представить в виде
представить в виде 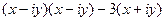
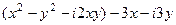 =
= 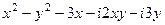 =
=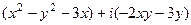
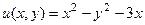 .
. 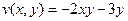 .
.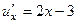 .
. 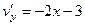 , они противоположны, а должны совпадать.
, они противоположны, а должны совпадать.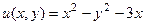 .
. 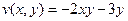 .
.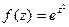 представить в виде
представить в виде 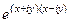 =
= 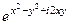 =
= 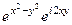
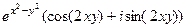 =
=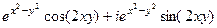 .
.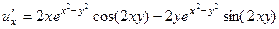
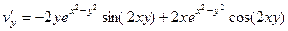
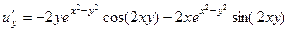
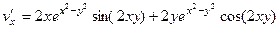
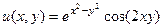 ,
, 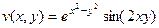 .
.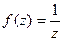 представить в виде
представить в виде 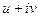 , проверить условия Коши-Римана.
, проверить условия Коши-Римана.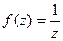 =
= 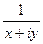 =
= 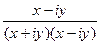
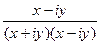 =
= 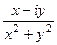 =
= 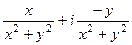 ,
,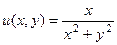 ,
, 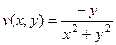 .
. 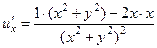 =
= 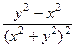
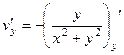 =
= 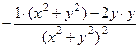 =
= 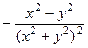 =
= 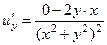 ,
, 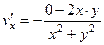 =
= 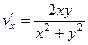 , они противоположны, второе условие выполнено.
, они противоположны, второе условие выполнено.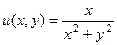 ,
, 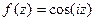 представить в виде
представить в виде 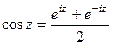 , то
, то 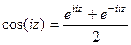 =
=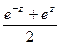 =
= 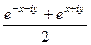 =
= 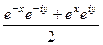
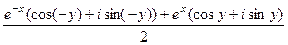 =
=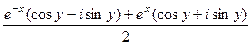 =
=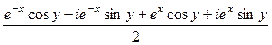 =
=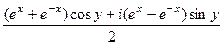 =
= 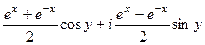 ,
,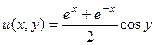 ,
, 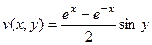 .
.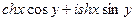 .
.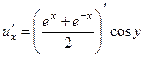 =
= 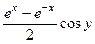
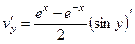 =
= 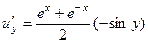
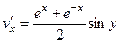 , они противоположны, второе условие выполнено.
, они противоположны, второе условие выполнено.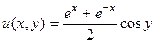 ,
, 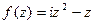 представить в виде
представить в виде 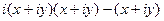 =
=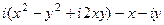 =
= 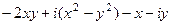 =
= 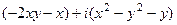 , тогда
, тогда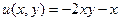 ,
, 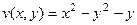 .
.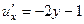
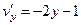 совпадают;
совпадают; 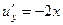
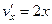 противоположные.
противоположные. 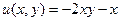 ,
, 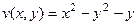 .
.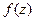 по разложению
по разложению 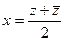 ,
, 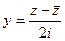 .
.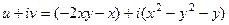 . Восстановить функцию
. Восстановить функцию 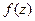 . (обратная к задаче 27).
. (обратная к задаче 27).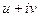 .
.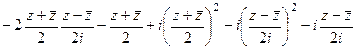 =
=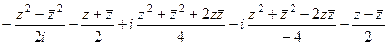 =
= =
=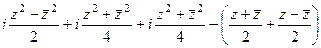 =
=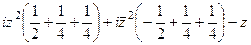 =
= 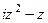
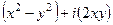 . Найти вид
. Найти вид 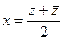 ,
, 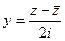 .
.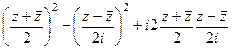 =
= 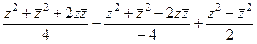 =
=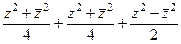 =
= 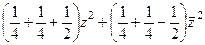 =
= 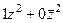 =
= 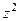 . Итак,
. Итак, 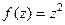 .
.


