
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциальные уравнения I порядка однородные
Уравнение вида Решение уравнения ищем с помощью замены переменной:
Пример 5.3. Найти общее решение ДУ: Решение. Сделаем замену Подставим значения
Разделим переменные и интегрируем:
Сделаем замену переменной:
То есть, Пример 5.4. Найти общее решение ДУ: Решение. ДУ можно записать в виде Сделаем замену переменной Подставим значения
Сделаем обратную замену переменной и получим общее решение ДУ: Дифференциальные уравнения I порядка линейные
Решение линейного ДУ уравнение (5.10) ищем в виде произведения двух функций
Функцию
Из первого уравнения находим переменную v:
Из второго уравнения находим переменную u:
Пример 5.5. Найти общее решение ДУ: Решение. Решение ищем в виде произведения двух функций Подставляя в
Сведем это уравнение к системе уравнений: Из первого уравнения системы находим функцию v:
Из второго уравнения системы найдем переменную u:
Находим общее решение линейного ДУ первого порядка:
Пример 5.6. Найти общее решение ДУ: Решение. Решение ищем в виде произведения функций
Приведем уравнение к системе ДУ: Из первого уравнения системы
Из второго уравнения системы имеем:
Находим общее решение линейного ДУ первого порядка:
Основные понятия дифференциальных уравнений второго порядка Дифференциальное уравнение второго порядка
можно решить путем понижения порядка и интегрированием. Так
5.5. Дифференциальные уравнения второго порядка Дифференциальное уравнение второго порядка
которое не содержит явно неизвестную функцию у, с помощью подстановки
сводится к уравнению первого порядка относительно функции р (х). Решив это уравнение, найдем Пример 5.7. Найти общее решение дифференциального уравнения Решение. Это уравнение является дифференциальным уравнением второго порядка, которое допускает понижение порядка. Интегрируя его, получим Пример 5.8. Найти общее решение дифференциального уравнения Решение. Данное дифференциальное уравнение второго порядка не содержит явно неизвестную функцию у. Поэтому следует воспользоваться подстановкой (5.16): Полученное уравнение является линейным дифференциальным уравнением первого порядка относительно р. Найдем его решение методом вариации произвольной постоянной, полагая Предположим, что в полученном решении произвольная постоянная С является неизвестной функцией от переменной х, т.е.
Решение (5.5) подставим в неоднородное дифференциальное уравнение, для чего вначале найдем производную Это дифференциальное уравнение с разделяющимися переменными, разделив которые получим: Возвращаясь к искомой функции у, получим Пример 5.9. Найти общее решение дифференциального уравнения Решение. Данное дифференциальное уравнение второго порядка не содержит явно неизвестную функцию у. Поэтому следует воспользоваться подстановкой (5.16): Полученное уравнение является дифференциальным уравнением первого порядка c разделяющимися переменными, разделив которые получим Возвращаясь к искомой функции у, получим имеем уравнения второго порядка будет иметь вид: 5.5. Дифференциальные уравнения второго порядка Дифференциальное уравнение второго порядка
которое не содержит явно переменную х, с помощью подстановки
сводится к уравнению первого порядка Его общее решение можно получить в виде Пример 5.10. Найти общее решение дифференциального уравнения Решение. Данное уравнение является дифференциальным уравнением второго порядка, которое не содержит явно переменную х. Решим его с помощью подстановки (5.16): После возвращения к переменной у, получим вновь дифференциальное уравнение первого порядка с разделяющимися переменными: Разделив переменные, получим
Пример 5.11. Найти общее решение дифференциального уравнения Решение. Данное уравнение является дифференциальным уравнением второго порядка, которое не содержит явно переменную х. Решим его с помощью подстановки (5.16): Разделив переменные, получим
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 93; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.169.94 (0.023 с.) |
 такая, что:
такая, что:
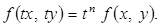
 называется однородным, если функции
называется однородным, если функции 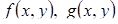 - однородные функции одного порядка.
- однородные функции одного порядка.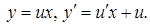
 .
.
 в ДУ.
в ДУ.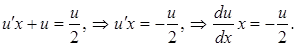



 .
.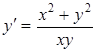 ,
,  .
.

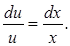

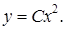

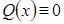 , то линейное ДУ называется однородным.
, то линейное ДУ называется однородным.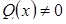 , то линейное ДУ называется неоднородным.
, то линейное ДУ называется неоднородным.
 Подставляя, получим уравнение:
Подставляя, получим уравнение:
 можно выбрать произвольно, то есть приведем уравнение к системе ДУ уравнений:
можно выбрать произвольно, то есть приведем уравнение к системе ДУ уравнений: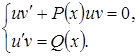



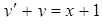 .
. тогда
тогда 


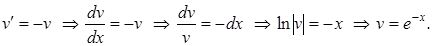

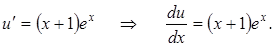

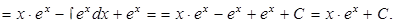

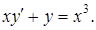
 Подставляя, получим уравнение:
Подставляя, получим уравнение:

 находим функцию v:
находим функцию v:



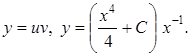
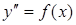 (5.14)
(5.14) , где С 1 – произвольная постоянная. Интегрируя еще раз, получим общее решение дифференциального уравнения (14) в виде
, где С 1 – произвольная постоянная. Интегрируя еще раз, получим общее решение дифференциального уравнения (14) в виде  , которое содержит две произвольных постоянных С 1 и С 2.
, которое содержит две произвольных постоянных С 1 и С 2.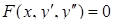 .
. , (5.15)
, (5.15) ,
,  (5.16)
(5.16) или
или 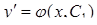 . Таким образом, получаем уравнение первого порядка относительно неизвестной функции у, решение которого будет иметь вид
. Таким образом, получаем уравнение первого порядка относительно неизвестной функции у, решение которого будет иметь вид  .
.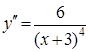 , а также частное решение, удовлетворяющее начальным условиям
, а также частное решение, удовлетворяющее начальным условиям 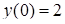 ,
,  .
. или
или  . Интегрируя еще раз полученное дифференциальное уравнение первого порядка (5.3)
. Интегрируя еще раз полученное дифференциальное уравнение первого порядка (5.3)  , найдем общее решение исходного дифференциального уравнения второго порядка
, найдем общее решение исходного дифференциального уравнения второго порядка  . Для нахождения частного решения заданного дифференциального уравнения, удовлетворяющего начальным условиям
. Для нахождения частного решения заданного дифференциального уравнения, удовлетворяющего начальным условиям  = 1. В результате получим систему уравнений
= 1. В результате получим систему уравнений 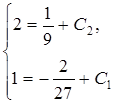 , решив которую, найдем
, решив которую, найдем 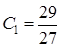 ,
, 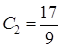 . Затем найденные значения произвольных постоянных подставим в общее решение дифференциального уравнения (5.4) и получим решение рассматриваемой задачи Коши, т.е. частное решение заданного дифференциального уравнения, удовлетворяющее начальным условиям
. Затем найденные значения произвольных постоянных подставим в общее решение дифференциального уравнения (5.4) и получим решение рассматриваемой задачи Коши, т.е. частное решение заданного дифференциального уравнения, удовлетворяющее начальным условиям 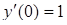 , в виде:
, в виде: 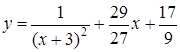 .
.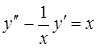 .
.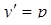 ,
,  , тогда исходное уравнение примет вид
, тогда исходное уравнение примет вид 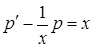 .
.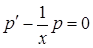 , откуда разделив переменные, получим
, откуда разделив переменные, получим  , затем после интегрирования найдем
, затем после интегрирования найдем  .
. .
.  . В результате получим равенство
. В результате получим равенство 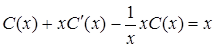 или после преобразований имеем
или после преобразований имеем  .
. , откуда имеем
, откуда имеем  . Поставив полученное решение в формулу (5.5), найдем общее решение линейного дифференциального уравнения
. Поставив полученное решение в формулу (5.5), найдем общее решение линейного дифференциального уравнения 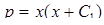 .
. , откуда имеем
, откуда имеем  . Тогда общее решение данного дифференциального уравнения второго порядка будет иметь вид
. Тогда общее решение данного дифференциального уравнения второго порядка будет иметь вид  .
.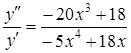 .
. ,
,  .
.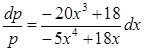 . После интегрирования найдем
. После интегрирования найдем 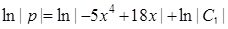 ,
, 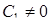 или
или  .
.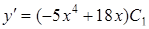 , откуда
, откуда . Тогда общее решение данного дифференциального
. Тогда общее решение данного дифференциального .
. .
.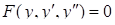 , (5.17)
, (5.17)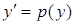 ,
,  ,
, 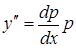 (5.18)
(5.18) относительно функции р, зависящей от переменной у.
относительно функции р, зависящей от переменной у. или
или 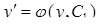 , а значит после разделения переменных
, а значит после разделения переменных  . Интегрируя последнее равенство, получим общий интеграл дифференциального уравнения (5.17)
. Интегрируя последнее равенство, получим общий интеграл дифференциального уравнения (5.17) 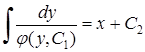 .
. .
. ,
,  и будет являться дифференциальным уравнением первого порядка с разделяющимися переменными, разделив которые получим
и будет являться дифференциальным уравнением первого порядка с разделяющимися переменными, разделив которые получим 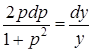 . Затем после интегрирования имеем
. Затем после интегрирования имеем 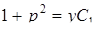 .
. .
. , откуда найдем
, откуда найдем  . Это и будет общий интеграл данного дифференциального уравнения второго порядка.
. Это и будет общий интеграл данного дифференциального уравнения второго порядка. .
.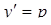 ,
,  и будет являться дифференциальным уравнением первого порядка с разделяющимися переменными, разделив которые получим
и будет являться дифференциальным уравнением первого порядка с разделяющимися переменными, разделив которые получим  . Затем после интегрирования имеем
. Затем после интегрирования имеем  . После возвращения к переменной у, получим вновь дифференциальное уравнение первого порядка с разделяющимися переменными:
. После возвращения к переменной у, получим вновь дифференциальное уравнение первого порядка с разделяющимися переменными:  .
. , откуда найдем
, откуда найдем  или
или 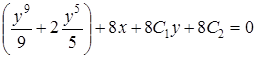 . Это и будет общий интеграл данного дифференциального уравнения второго порядка.
. Это и будет общий интеграл данного дифференциального уравнения второго порядка.


