Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы решения линейных уравнений
Рассмотрим систему трех линейных уравнений с тремя неизвестными
Чтобы решить систему (1.17), из коэффициентов при неизвестных и свободных членов составим определители третьего порядков Определитель (D), составленный из коэффициентов при неизвестных называется главным определителем системы и имеет вид:
Определители
При решении системы уравнений (1.17) могут быть три случая:
Пример 1.11. Решить систему уравнений по формулам Крамера:
Решение. а) Находим определители системы
По формулам Крамера (1.19) имеем:
Возьмем второе и третье уравнение системы: Эти уравнения содержат отличный от нуля минор второго порядка:
Имеем где Система имеет бесчисленное множество решений: Метод обратной матрицы Задана система, содержащая
Введем матрицы: Матрицу
Допустим, что матрица
Замечание. Решение системы уравнений в матричной форме возможно только тогда, когда матрица системы квадратная и невырожденная. Пример 1.12. Решить систему уравнений матричным методом:
Решение. Имеем Найдем определитель матрицы Найдем обратную матрицу
По формуле (1.15) обратная матрица имеет вид:
По формуле (1.22) находим решение системы линейных уравнений:
То есть, Метод Гаусса Метод последовательного исключения неизвестных. С помощью элементарных преобразований систему уравнений приводят к треугольному виду, из которой последовательно находят все переменные. При решении системы линейных уравнений удобнее приводить к треугольному виду расширенную матрицу этой системы, то есть матрицу, образованную присоединением к матрице коэффициентов столбец свободных членов.
Пример 1.13. Решить системы линейных уравнений методом Гауcса:
Решение.
~ Таким образом, получим систему линейных уравнений:
Которая имеет единственное решение:
Отсюда система линейных уравнений имеет вид:
В последнем уравнении свободный член равен двум, а коэффициенты при неизвестных равны нулю, то есть система несовместна.
|
||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 62; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.174.156 (0.008 с.) |
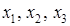 :
: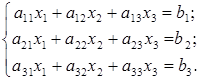
 .
.
 образовываются из определителя
образовываются из определителя  (1.17) соответственно заменою первого, второго и третьего столбцов столбцом свободных членов:
(1.17) соответственно заменою первого, второго и третьего столбцов столбцом свободных членов: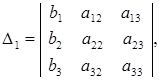
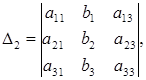

 тогда система (1.17) имеет единственное решение, которое можно найти по формулам Крамера (1.19):
тогда система (1.17) имеет единственное решение, которое можно найти по формулам Крамера (1.19):

 и хотя бы один из определителей
и хотя бы один из определителей  не равен нулю, то система (1.17) не имеет решений.
не равен нулю, то система (1.17) не имеет решений.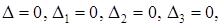 то система (1.17) имеет бесчисленное множество решений.
то система (1.17) имеет бесчисленное множество решений.


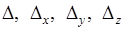 :
:
 ,
, 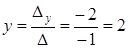 ,
, 
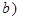 Находим определитель системы
Находим определитель системы 
 (согласно свойству определителей 2).
(согласно свойству определителей 2).

 ;
;  ;
;  ,
, - произвольное действительное число.
- произвольное действительное число. ,
,  ,
, 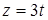 .
.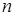 линейных уравнений с
линейных уравнений с 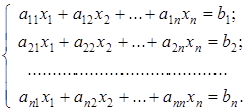
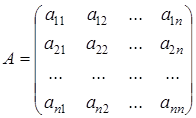 ;
; 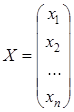 ;
; 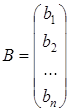 .
.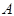 , составленную из коэффициентов системы (1.20), называют основной матрицей, матрицу-столбец
, составленную из коэффициентов системы (1.20), называют основной матрицей, матрицу-столбец 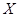 – матрицею неизвестных, а матрицу-столбец
– матрицею неизвестных, а матрицу-столбец 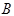 – матрицею свободных членов. Согласно правилу умножения двух матриц, систему (1.20) можно записать одним матричным уравнением с неизвестной матрицей
– матрицею свободных членов. Согласно правилу умножения двух матриц, систему (1.20) можно записать одним матричным уравнением с неизвестной матрицей 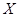 :
: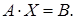
 . Умножим обе части равенства (1.21) на
. Умножим обе части равенства (1.21) на 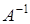 слева:
слева:  . Поскольку
. Поскольку 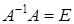 и
и 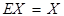 , то матричная запись решения системы имеет вид:
, то матричная запись решения системы имеет вид:
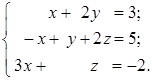
 ;
; 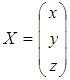 ;
; 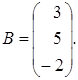
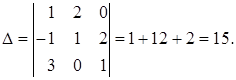
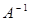 к матрице
к матрице  Для этого выпишем алгебраические дополнения к матрице
Для этого выпишем алгебраические дополнения к матрице 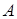 по формуле (1.14):
по формуле (1.14):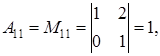

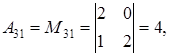

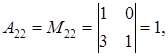
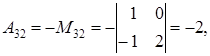

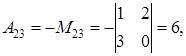
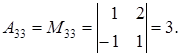
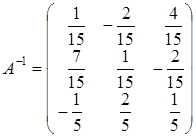 .
.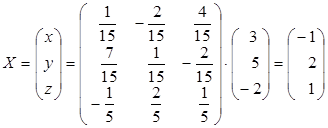 .
. ,
, 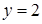 ,
, 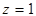 .
.
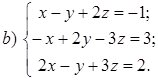
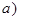 Выполним элементарные преобразования над строками расширенной матрицы данной системы:
Выполним элементарные преобразования над строками расширенной матрицы данной системы: ~
~  ~
~  ~
~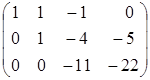 ~
~ 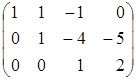 .
.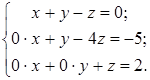
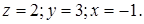
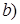 Имеем:
Имеем: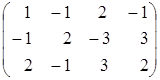 ~
~ 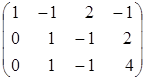 ~
~ 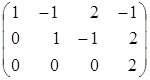 .
.