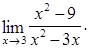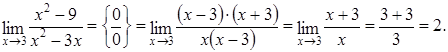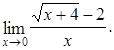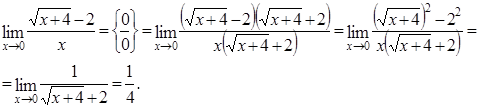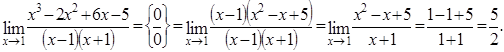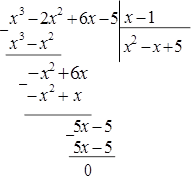Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 1. Элементы линейной алгебрыСтр 1 из 7Следующая ⇒
И.В. Гречина
МАТЕМАТИКА
(ЭЛЕКТРОННЫЙ КОНСПЕКТ ЛЕКЦИЙ (КРАТКИЙ))
Донецк 2019 ГО ВПО «ДонНУЭТ»
СОДЕРЖАНИЕ: ВВЕДЕНИЕ. 5 Смысловой модуль І 1.3. Системы линейных уравнений. 13 1.4. Методы решения линейных уравнений.. 13 Лекция 2. ПРЕДЕЛЫ. НЕПРЕРЫВНОСТЬ ФУНКЦИИ. 18 2.1. Функции. 18 2.2. Предел числовой последовательности и функции. 19 2.3. Раскрытие неопределенностей. 20 2.4. Замечательные пределы. 22 2.5. Непрерывность функции. 23 Лекция 3. дифференциальное исчисление. 25 3.1. Дифференциальное исчисление функции одной переменной. 25 3.2. Производная сложной функции. 26 3.3. Производная неявной функции. 27 3.4. Производная параметрически заданной функции. 27 3.5. Логарифмическое дифференцирование. 28 3.6. Производная функции старших порядков. 29 3.7. Основные понятия. 30 3.8. Исследование функции. 32 Лекция 4. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ. 36 4.1. Основные понятия. Таблица интегралов. 36 4.2. Метод замены переменной. 37 4.3. Метод интегрирования по частям. 38 4.4. Определенный интеграл. Его свойства. 40 4.5. Несобственный интеграл с бесконечными пределами. 41 4.6. Несобственный интеграл от разрывных функций. 42 Смысловой модуль ІІ 44 Дифференциальные уравнения. Ряды. Основы теории вероятности и математической статистики. 44 Лекция 5. Дифференциальные уравнения.. 44 5.1. Дифференциальные уравнения с разделяющимися переменными 44 5.2. Дифференциальные уравнения I порядка однородные. 46 5.3. Дифференциальные уравнения I порядка линейные. 47 5.4. Основные понятия дифференциальных уравнений второго порядка 48 5.5. Дифференциальные уравнения второго порядка 5.5. Дифференциальные уравнения второго порядка 5.7. Линейные дифференциальные уравнения II порядка с постоянными коэффициентами. 52 ТЕМА 6. ЧИСЛОВЫЕ И СТЕПЕННЫЕ РЯДЫ. 6.1. Основные понятия. 6.2. Необходимое условие сходимости числового ряда. 6.3. Достаточные условия сходимости числового ряда. 6.4. Знакопеременные ряды. 6.5. Признак Лейбница. 6.6. Степенные ряды. ЛЕКЦИЯ 7. ОСНОВНЫЕ ПОНЯТИЯ И ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ. 7.1. Основные понятия теории вероятностей. 7.2. Теоремы сложения. 7.3. Теоремы умножения. 7.4. Формула полной вероятности. 7.5. Формулы Бейеса. Ошибка! Закладка не определена. Тема 8. Повторные НЕЗАВИСИМЫЕ испытания.. Ошибка! Закладка не определена.
8.1. Формула Бернулли. Ошибка! Закладка не определена. 8.2. Формула Пуассона. Ошибка! Закладка не определена. 8.3. Локальная теорема Лапласа. Ошибка! Закладка не определена. 8.4. Интегральная теорема Лапласа. Ошибка! Закладка не определена. Тема 9. Случайные величины и их характеристики.. Ошибка! Закладка не определена. 9.1. Понятие случайной величины. Ошибка! Закладка не определена. 9.2. Функция распределения и плотность распределения. Ошибка! Закладка не определена. 9.3. Числовые характеристики случайных величин. Ошибка! Закладка не определена. ПРИЛОЖЕНИЕ 1. 55 ПРИЛОЖЕНИЕ 2. 59 ПРИЛОЖЕНИЕ 3. Ошибка! Закладка не определена. ПРИЛОЖЕНИЕ 4. Ошибка! Закладка не определена. РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА..
ЛЕКЦИЯ 1. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ План: 1.1. Матрицы 1.2. Определители 1.3. Системы линейных уравнений 1.4. Методы решения линейных уравнений
Матрицы
Виды матриц:
Символы Элементы
Треугольная матрица сверху Треугольная матрица снизу
Свойства операции транспонирования:
Например:
Действия над матрицами:
Пример 1.1. Найти сумму матриц Решение. Так как матрицы
Пример 1.2. Найти произведение матрицы Решение.
Замечание. Операция умножения двух матриц возможна, если количество столбцов первой матрицы Замечание. Пример 1.3. Найти произведение матриц Решение. Количество столбцов матрицы
Пример 1.4. Найти произведение двух матриц Решение. Количество столбцов матрицы
Квадратной матрице можно поставить в соответствие число, которое называется определителем этой матрицы. Прямоугольная матрица определителя не имеет. В матрице
Определители
Основные свойства определителей: 1. Значение определителя не изменится, если все его строки заменить соответствующими столбцами (столбцы при этом заменяются соответствующими строками). 2. Определитель, имеющий нулевую строку (столбец) равен нулю. 3. Если определитель имеет две одинаковые строки (столбцы), то он равен нулю. 4. При перестановке двух строк (столбцов) определитель изменяет знак. 5. Общий множитель элементов некоторого столбца (строки) можно вынести за знак определителя. 6. Для умножения определителя 7. Определитель не меняется, если к элементам одной строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на это число. 8. Определитель, имеющий две пропорциональные строки (столбцы), равен нулю. 9. Если в определителе некоторая (например, і -й) строка является суммой двух слагаемых, то этот определитель можно представить в виде суммы двух определителей, у которых все строки, кроме і -й, будут такие же, как в данном определителе, а і -я строка первого определителя состоит из первого слагаемого і -й строки исходного определителя, а і -я строка второго определителя состоит из второго слагаемого і -й строки исходного определителя.
Например, минором элемента
На практике, определители 3-го и старше порядков находятся по теореме Лапласа разложением по элементам строки (столбца).
Например, разложение определителя (1.13) по элементам второго столбца имеет вид:
де
Определитель третьего порядка можно находить по правилу треугольника или правилу Саррюса (рис. 1.1).
Рисунок 1.1 – Правило треугольников
Можно воспользоваться правилом дописывания двух столбцов для вычисления определителя 3-го порядка (рис. 1.2) по алгоритму: 1. Дописывают к определителю с правой стороны два первых его столбца. 2. Начиная с левого верхнего угла перемножают все элементы, расположенные вдоль главной диагонали определителя и складывают с аналогичными произведениями всех элементов, которые находятся на двух других диагоналях, параллельных главной. 3. Аналогично перемножают все элементы, которые расположены на диагоналях, параллельных побочной, начиная с верхнего правого угла дополненного «определителя», и три полученных произведения вычитают из предыдущей суммы.
Рисунок 1.2 – Правило дописывания двух столбцов
Пример 1.5. Вычислить определитель:
Решение. Используем формулу (1.12): Используем правило треугольников (рисунок 1.1):
Пример 1.6. Решить уравнение Решение. Вычислим определитель по правилу Саррюса (рис. 1.1):
Пример 1.7. Вычислить определитель по теореме Лапласа:
Решение. Разложим определитель по элементам первой строки:
Пример 1.8. Нераскрываяопределитель, доказать равенство:
Доказательство. Добавим к элементам первого столбца соответствующие элементы третьего столбца (согласно свойству определителей 7), получим:
Этот определитель равен нулю, согласно свойству определителей 3. Пример 1.9. Доказать, что определитель равен нулю:
Доказательство. Используем свойства определителей. Элементы четвертого столбца определителя совпадают с элементами первого столбца, умноженными на 2. Из свойства определителей 8 следует, что определитель равен нулю.
где Пример 1.10. Найти обратную матрицу к матрицам:
Решение.
Запишем обратную матрицу:
Сделаем проверку:
b) Находим определитель матрицы
Запишем обратную матрицу по формуле (1.15):
Системы линейных уравнений Системою m линейных уравнений с n неизвестными называется система вида:
где
Метод обратной матрицы Задана система, содержащая
Введем матрицы: Матрицу
Допустим, что матрица
Замечание. Решение системы уравнений в матричной форме возможно только тогда, когда матрица системы квадратная и невырожденная. Пример 1.12. Решить систему уравнений матричным методом:
Решение. Имеем Найдем определитель матрицы Найдем обратную матрицу
По формуле (1.15) обратная матрица имеет вид:
По формуле (1.22) находим решение системы линейных уравнений:
То есть, Метод Гаусса Метод последовательного исключения неизвестных. С помощью элементарных преобразований систему уравнений приводят к треугольному виду, из которой последовательно находят все переменные. При решении системы линейных уравнений удобнее приводить к треугольному виду расширенную матрицу этой системы, то есть матрицу, образованную присоединением к матрице коэффициентов столбец свободных членов.
Пример 1.13. Решить системы линейных уравнений методом Гауcса:
Решение.
~ Таким образом, получим систему линейных уравнений:
Которая имеет единственное решение:
Отсюда система линейных уравнений имеет вид:
В последнем уравнении свободный член равен двум, а коэффициенты при неизвестных равны нулю, то есть система несовместна.
Функции
Пример 2.1. Найти область определения функций:
Решение.
Пример 2.2. Найти область определения функции:
Решение. Первое слагаемое
Примеры четных функций: Примеры нечетных функций: Существуют функции общего вида (например, Раскрытие неопределенностей Неопределенность вида
Пример 2.3. Найти предел Решение.
Пример 2.4. Найти предел Решение.
Пример 2.5. Найти предел Решение.
Пример 2.6. Найти предел Решение.
Пример 2.7. Найти предел Решение.
Неопределенность вида Для рациональных функций неопределенность этого вида раскрывают выделением в числителе и знаменателе двухчлена Для иррациональных функций – необходимо числитель и знаменатель умножить на сопряженное выражение для иррационального, выполнить преобразования и вычислить предел. Пример 2.8. Найти предел Решение. Раскладываем на множители по формуле сокращенного умножения числитель и сокращаем дробь: Пример 2.9. Найти предел Решение. Числитель и знаменатель умножим на сопряженное выражение к числителю, затем свернем формулу сокращенного умножения в числителе и выполним преобразования:
Пример 2.10. Найти предел Решение. Выделим критический множитель из числителя и знамена теля, выполнив потом сокращение дроби:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 173; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.41.187 (0.191 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 . 49
. 49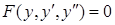 . 51
. 51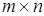 называется прямоугольная таблица чисел (элементов матрицы), содержащая
называется прямоугольная таблица чисел (элементов матрицы), содержащая 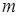 строк и
строк и 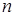 столбцов:
столбцов:
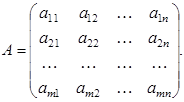
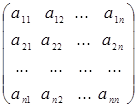
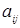 – э лементы матрицы: первый индекс
– э лементы матрицы: первый индекс  показывает номер строки, второй индекс
показывает номер строки, второй индекс 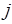 – номер столбца на пересечении которых расположен данный элемент.
– номер столбца на пересечении которых расположен данный элемент. квадратной матрицы образуют главную диагональ, а элементы
квадратной матрицы образуют главную диагональ, а элементы 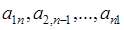 – побочную диагональ.
– побочную диагональ.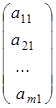


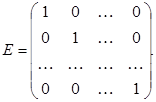

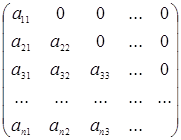
 и
и 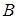 одинаковой размерности называются равными, если равны их соответствующие элементы
одинаковой размерности называются равными, если равны их соответствующие элементы 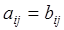 .
.
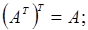


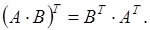
 , тогда
, тогда 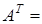
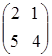 ;
; 
 .
. одинаковой размерности называется матрица
одинаковой размерности называется матрица 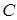 такой же размерности, элементы которой равны
такой же размерности, элементы которой равны 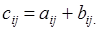
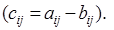

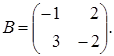

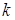 есть матрица
есть матрица 
 на число
на число 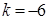 .
.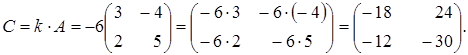
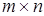 на матрицу
на матрицу 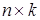 есть матрица
есть матрица  , размерности
, размерности 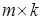 , элементы которой находятся по формуле
, элементы которой находятся по формуле 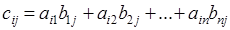 (то есть элемент
(то есть элемент 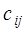 , расположенный в і -й строке и j -м столбце матрицы
, расположенный в і -й строке и j -м столбце матрицы 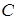 , равен сумме произведений элементов
, равен сумме произведений элементов 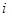 -й строки матрицы
-й строки матрицы 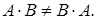
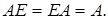


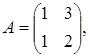


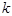 -го порядка, где
-го порядка, где 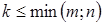 . Определители таких матриц называются минорами
. Определители таких матриц называются минорами  .
.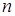 - называется число или алгебраическое выражение, записанное в виде алгебраических выражений, содержащее
- называется число или алгебраическое выражение, записанное в виде алгебраических выражений, содержащее 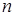 строк и
строк и 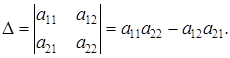

 – го порядка на число, достаточно все элементы некоторого столбца (стоки), умножить на это число.
– го порядка на число, достаточно все элементы некоторого столбца (стоки), умножить на это число.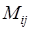 элемента
элемента 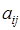 определителя
определителя 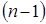 – го порядка, образованный из исходного определителя в результате вычеркивания
– го порядка, образованный из исходного определителя в результате вычеркивания 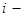 й строки и
й строки и  столбца, содержащих элемент
столбца, содержащих элемент 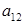 есть определитель
есть определитель  , получаемый из определителя (1.13), вычеркиванием в нем первой строки и второго столбца.
, получаемый из определителя (1.13), вычеркиванием в нем первой строки и второго столбца. элемента
элемента 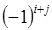 , то есть:
, то есть:
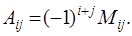
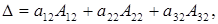
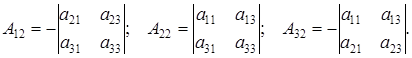














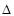 =
=  +
+ 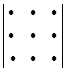 +
+ 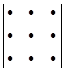 -
- 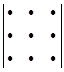 .
.

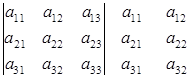 -
- 
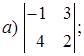
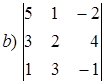 .
.
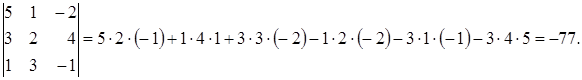


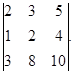
 , тогда
, тогда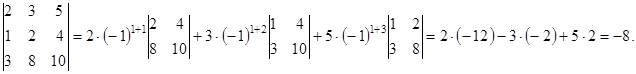
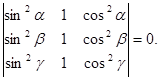
 .
.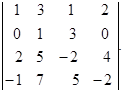
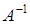 называется обратной к квадратичной матрице
называется обратной к квадратичной матрице 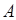 , если выполняется условие:
, если выполняется условие: 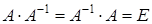 , где
, где 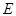 – единичная матрица.
– единичная матрица.
 называется вырожденной, если ее определитель равен нулю (
называется вырожденной, если ее определитель равен нулю (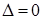 ) и невырожденной, если
) и невырожденной, если 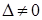 .
.
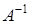 необходимо и достаточно, чтобы матрица
необходимо и достаточно, чтобы матрица  была невырожденной.
была невырожденной.
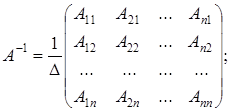
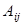 – алгебраические дополнения элементов
– алгебраические дополнения элементов 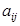 определителя матрицы
определителя матрицы 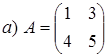 ,
, 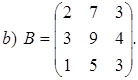
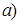 Находим определитель матрицы
Находим определитель матрицы 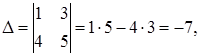
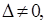 то есть матрица невырожденная. Обратную матрицу находим по формуле (1.15). Для этого вычислим алгебраические дополнения по формуле (1.14):
то есть матрица невырожденная. Обратную матрицу находим по формуле (1.15). Для этого вычислим алгебраические дополнения по формуле (1.14):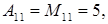

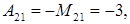
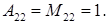
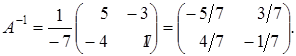
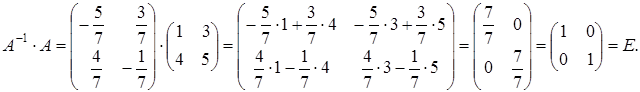
 матрица невырожденная. Вычислим алгебраические дополнения по формуле (1.14):
матрица невырожденная. Вычислим алгебраические дополнения по формуле (1.14):

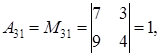
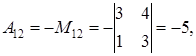
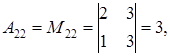

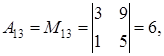
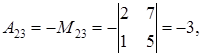
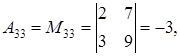
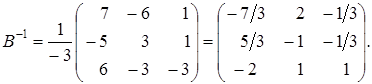
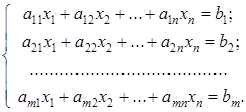
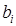 – свободные члены,
– свободные члены, 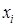 – неизвестные,
– неизвестные, 
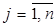 .
.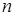 линейных уравнений с
линейных уравнений с 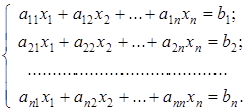
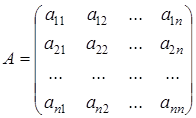 ;
; 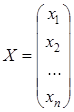 ;
; 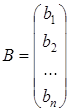 .
.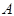 , составленную из коэффициентов системы (1.20), называют основной матрицей, матрицу-столбец
, составленную из коэффициентов системы (1.20), называют основной матрицей, матрицу-столбец 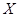 – матрицею неизвестных, а матрицу-столбец
– матрицею неизвестных, а матрицу-столбец 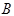 – матрицею свободных членов. Согласно правилу умножения двух матриц, систему (1.20) можно записать одним матричным уравнением с неизвестной матрицей
– матрицею свободных членов. Согласно правилу умножения двух матриц, систему (1.20) можно записать одним матричным уравнением с неизвестной матрицей 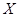 :
: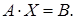
 . Умножим обе части равенства (1.21) на
. Умножим обе части равенства (1.21) на 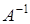 слева:
слева:  . Поскольку
. Поскольку 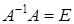 и
и 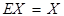 , то матричная запись решения системы имеет вид:
, то матричная запись решения системы имеет вид:
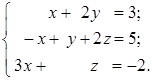
 ;
; 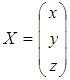 ;
; 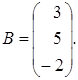
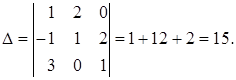
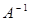 к матрице
к матрице  Для этого выпишем алгебраические дополнения к матрице
Для этого выпишем алгебраические дополнения к матрице  по формуле (1.14):
по формуле (1.14):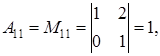

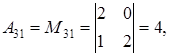

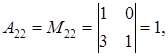
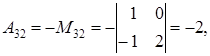

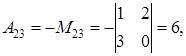
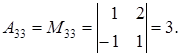
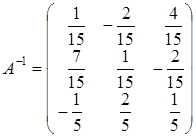 .
.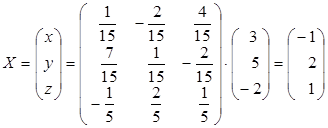 .
. ,
, 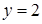 ,
, 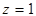 .
.
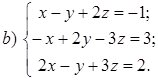
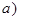 Выполним элементарные преобразования над строками расширенной матрицы данной системы:
Выполним элементарные преобразования над строками расширенной матрицы данной системы: ~
~  ~
~  ~
~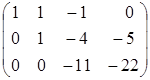 ~
~ 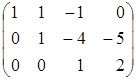 .
.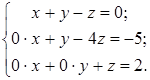
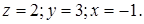
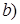 Имеем:
Имеем: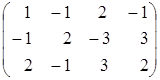 ~
~ 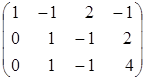 ~
~ 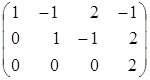 .
.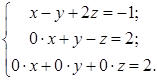
 от переменной
от переменной 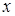 называется функцией, если каждому значению
называется функцией, если каждому значению 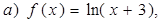


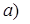 Выражение под знаком логарифма всегда положительно, поэтому
Выражение под знаком логарифма всегда положительно, поэтому 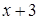 >0. Тогда область определения функции имеет вид
>0. Тогда область определения функции имеет вид 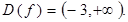
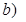 Функция
Функция 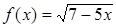 определена, если подкоренное выражение неотрицательно, то есть
определена, если подкоренное выражение неотрицательно, то есть 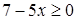 или
или 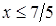 . Тогда
. Тогда 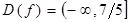 .
.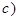 Функция
Функция  определена, если ее знаменатель не равен нулю, то есть
определена, если ее знаменатель не равен нулю, то есть 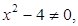 или
или 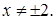 Тогда
Тогда 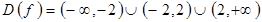 .
.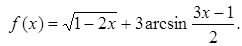
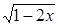 принимает действительные значения при
принимает действительные значения при 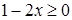 , а другое при
, а другое при 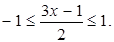 Решив полученные неравенства одновременно, получим область значений функции
Решив полученные неравенства одновременно, получим область значений функции 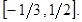
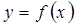 определенная на множестве
определенная на множестве 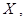 называется четной, если для любого
называется четной, если для любого  выполняется равенство
выполняется равенство 
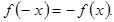

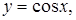
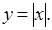
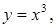


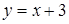 ).
).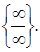
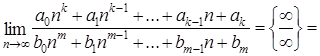
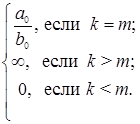

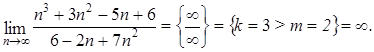
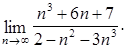

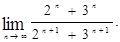
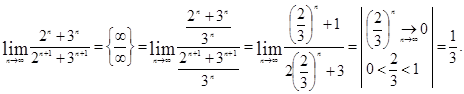

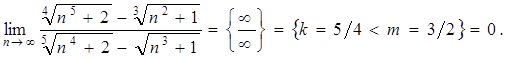
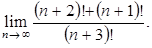
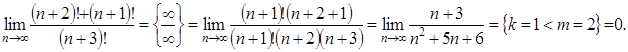
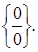
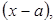 последующим сокращением на него и вычислением предела.
последующим сокращением на него и вычислением предела.