
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 2. Пределы. Непрерывность функции.
Функции
Пример 2.1. Найти область определения функций:
Решение.
Пример 2.2. Найти область определения функции:
Решение. Первое слагаемое
Примеры четных функций: Примеры нечетных функций: Существуют функции общего вида (например, Предел числовой последовательности и функции Последовательность по определению есть функция, то есть предел последовательности — отдельный случай предела функции. Наоборот, в некотором смысле предел функции может быть сведен к пределу последовательности. Поэтому теоремы о пределах последовательностей также выполняются для пределов функций.
Это записывают так:
Теорема. Связь между бесконечно-малыми и бесконечно-большими функциями. Если функция
Предельный переход при арифметических операциях
Раскрытие неопределенностей Неопределенность вида
Пример 2.3. Найти предел Решение.
Пример 2.4. Найти предел Решение.
Пример 2.5. Найти предел Решение.
Пример 2.6. Найти предел Решение.
Пример 2.7. Найти предел Решение.
Неопределенность вида Для рациональных функций неопределенность этого вида раскрывают выделением в числителе и знаменателе двухчлена Для иррациональных функций – необходимо числитель и знаменатель умножить на сопряженное выражение для иррационального, выполнить преобразования и вычислить предел. Пример 2.8. Найти предел Решение. Раскладываем на множители по формуле сокращенного умножения числитель и сокращаем дробь: Пример 2.9. Найти предел Решение. Числитель и знаменатель умножим на сопряженное выражение к числителю, затем свернем формулу сокращенного умножения в числителе и выполним преобразования:
Пример 2.10. Найти предел Решение. Выделим критический множитель из числителя и знамена теля, выполнив потом сокращение дроби:
Неопределенность вида Раскрывают умножением и делением выражения под знаком предела на сопряженное, в результате чего можно осуществить предельный переход выражения по правилам предельного перехода при Пример 2.12. Найти предел Решение. Умножаем и делим под знаком предела на сопряженное, затем применяем формулу сокращенного умножения и выполняем преобразования:
Пример 2.13. Найти предел Решение. Приведем к общему знаменателю две дроби, выполним преобразование в полученной дроби и вычислим предел:
Замечательные пределы Первый замечательный предел:
Следствия первого замечательного предела:
Второй замечательный предел:
Следствия второго замечательного предела:
Пример 2.14. Найти предел Решение. Используем следствия из первого замечательного предела, получим:
Решение. Используем следствия из первого замечательного предела, получим:
Пример 2.16. Найти предел Решение. Выполним преобразования для выделения единицы, а затем используем второй замечательный предел.
Непрерывность функции Функция непрерывна в точке х = х0 если: 1) она определена в точке х0, т.е. существует f(x0); 2) существует предел функции при х стремящемся к х0; 3) этот предел равен значению функции в точке х0.
Пример 2.17. Проверить на непрерывность функции:
Решение.
Если При
1. Шипачев В. С. Высшая математика: рекоменд. М-вом образования и науки РФ учебник для студ. высш. учеб. завед. / В. С. Шипачев; М-во образования и науки РФ. – Москва: Высш. шк., 2010. – 479 с.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 58; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.107.90 (0.055 с.) |
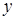 от переменной
от переменной 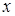 называется функцией, если каждому значению
называется функцией, если каждому значению 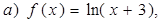


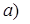 Выражение под знаком логарифма всегда положительно, поэтому
Выражение под знаком логарифма всегда положительно, поэтому 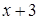 >0. Тогда область определения функции имеет вид
>0. Тогда область определения функции имеет вид 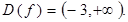
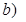 Функция
Функция 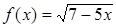 определена, если подкоренное выражение неотрицательно, то есть
определена, если подкоренное выражение неотрицательно, то есть 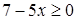 или
или 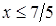 . Тогда
. Тогда 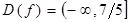 .
.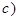 Функция
Функция  определена, если ее знаменатель не равен нулю, то есть
определена, если ее знаменатель не равен нулю, то есть 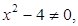 или
или 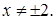 Тогда
Тогда 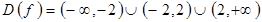 .
.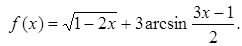
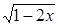 принимает действительные значения при
принимает действительные значения при 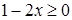 , а другое при
, а другое при 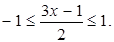 Решив полученные неравенства одновременно, получим область значений функции
Решив полученные неравенства одновременно, получим область значений функции 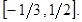
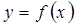 определенная на множестве
определенная на множестве 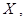 называется четной, если для любого
называется четной, если для любого  выполняется равенство
выполняется равенство 
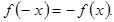

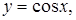
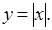
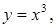


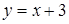 ).
). называется пределом функции
называется пределом функции 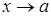 , если для любого малого положительного числа
, если для любого малого положительного числа 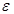 найдется такое число
найдется такое число  что для всех
что для всех 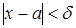 выполняется неравенство:
выполняется неравенство:
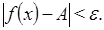
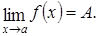
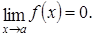

 есть бесконечно-большая, то функция
есть бесконечно-большая, то функция  будет бесконечно-малой.
будет бесконечно-малой.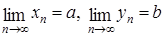 , то:
, то:



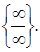
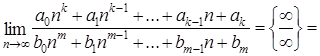
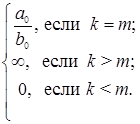

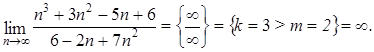
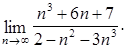

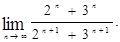
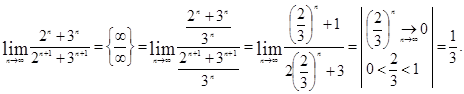

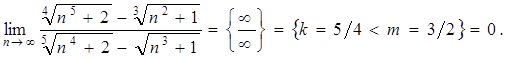
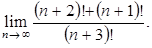
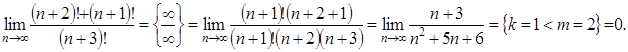
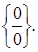
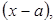 последующим сокращением на него и вычислением предела.
последующим сокращением на него и вычислением предела.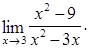
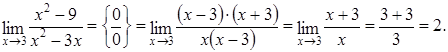
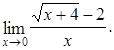
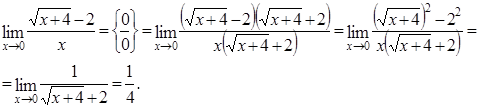
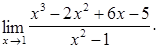
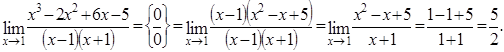
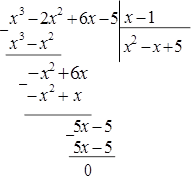
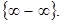
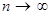 .
.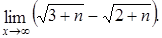

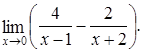
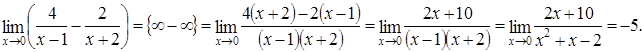
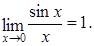
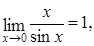
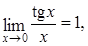



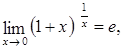
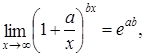



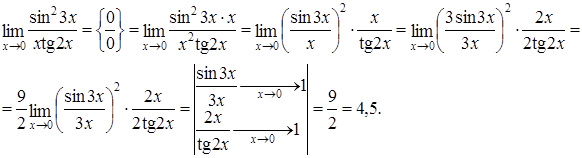 Пример 2.15. Найти предел
Пример 2.15. Найти предел 



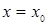 , в которой нарушается хотя бы одно из условий равенства:
, в которой нарушается хотя бы одно из условий равенства:
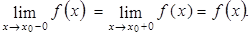
 называется точкою разрыва первого рода, если функция в этой точке имеет конечные односторонние пределы. В общем виде они разные.
называется точкою разрыва первого рода, если функция в этой точке имеет конечные односторонние пределы. В общем виде они разные.
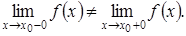
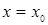 называется точкой устраненного разрыва функции
называется точкой устраненного разрыва функции  , если односторонние пределы функции равны:
, если односторонние пределы функции равны:
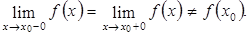
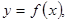 если в этой точке не существует хотя бы один из односторонних пределов (слева или справа).
если в этой точке не существует хотя бы один из односторонних пределов (слева или справа).
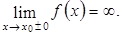

 Находим
Находим 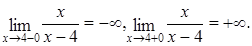 Функция при
Функция при  не имеет ни правого ни левого конечного предела. Отсюда,
не имеет ни правого ни левого конечного предела. Отсюда,  является точкой разрыва второго рода по условию (4.6).
является точкой разрыва второго рода по условию (4.6).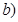 Если
Если  то
то 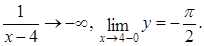
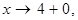 то
то 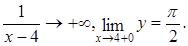
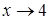 функция имеет разные односторонние пределы. Причем, по условию (4.4),
функция имеет разные односторонние пределы. Причем, по условию (4.4), 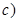 В точке
В точке  функция имеет неопределенность вида
функция имеет неопределенность вида  В других точках дробь сокращается на
В других точках дробь сокращается на  поскольку
поскольку  Отсюда, при
Отсюда, при 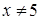
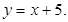 Легко показать, что
Легко показать, что 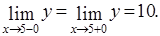 Таким образом, по условию (4.5), при х =5 функция имеет устраненный разрыв. Его можно устранить, если считать, что при
Таким образом, по условию (4.5), при х =5 функция имеет устраненный разрыв. Его можно устранить, если считать, что при 



