
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Производная и дифференцируемость функции
25. Найти производную функции: 1) 3) 5) 7) 9) 11) 13) 15) 26. а) Определить углы, под которыми графики функций: б) Написать уравнение касательной и нормали к кривой в) Доказать, что уравнение касательной к эллипсу г) Тело массой 100 кг движется прямолинейно по закону 27. Доказать тождество 28. Квадратный 3-х член 29. Доказать, что 30. Вычислить предел Указание. Применить формулу Тейлора. 31. Пусть 32. Пусть 33. Доказать, что при 34. При каком значении a функция 35. Пусть Указание. Применить формулу Тейлора. 36. Пусть
Доказать, что существует число Указание. Применить теорему Ролля. 37. Доказать, что функция дифференцируема на R. 38. Дана функция Существует ли производная функции в точке x =0? Будет ли эта функция непрерывной в точке x =0? 39. Исследовать на непрерывность и дифференцируемость функцию 40. На основании теоремы Лагранжа доказать неравенство 41. Доказать, что функция 42. Пусть функция Доказать, что существует точка
(Указание. Применить теорему Коши о среднем для функции 43. Пусть определена функция Применяя теорему Лагранжа для сегмента [0, x ] имеем Отсюда Если 44. Пусть функция График функции Построить график следующих функций 45. а) в) 46.
47. а) 48. 49. 50. Интегрирование 51. Вычислить неопределенный интеграл: 1) 4) 7) 10) 13) 16) 19) 22) 25) 28) 31) 52. Вычислить определенный интеграл: 1) 4) 7) 10) 13) 16) 19) 53. а) Вычислить площадь фигуры ограниченной линиями: 1) 2) 3) 4) 5) б) Найти площадь фигуры, ограниченной эллипсом; в) Найти длину кривой: 1) 2) 3) Ряды 54. Найти сумму ряда 55. Исследовать на сходимость: а) г) 56. Исследовать на абсолютную или условную сходимость: а) в) 57. Исследовать на равномерную сходимость функциональные последовательности: а) в) 58. Исследовать на равномерную сходимость функциональные ряды: а) в) 59. Пусть задана функция 60. Найти сумму степенного ряда 61. Найти круг сходимости степенного ряда. Будет ли аналитической его сумма в точке с? а) 62. Разложить функцию в ряд Тейлора в окрестности точки z0=2 и найти круг сходимости: а) 63. Вычислить приближенно число 64. Вычислить с точностью до 10-3 интеграл Теория функций 65. Установить биекцию между сегментом [0;1] и интервалом (0,1). 66. Доказать, что множество всех функций, непрерывных на [ а, b ], имеет мощность континуума. 67. Доказать, что множество всех функций (непрерывных и разрывных), заданных на сегменте [ a, b ], имеет мощность f, большую, чем мощность континуума, причем 68. Доказать, что множество всех точек разрыва монотонной функции, заданной на промежутке < a, b > не более чем счетно. 69. Дано множество
70. Доказать, что замыкание любого множества замкнуто. 71. Доказать, что множество замкнуто тогда и только, когда оно совпадает со своим замыканием. 72. Доказать, что граница любого множества замкнута, причем 73. Доказать, что если множество 74. Доказать, что расстояние между непересекающимися замкнутыми множествами строго положительно, если хотя бы одно из этих множеств ограничено. 75. Может ли быть интегрируемой по Риману на [ a, b ] функция, разрывная во всех точках некоторого непустого открытого множества 76. Доказать, что пространство 77. Доказать, что множество непрерывных функций, заданных на [ a, b ], всюду плотно в 78. Пусть функция 79. Доказать, что функция гармоничная в некоторой области и отличная от постоянной не может принимать (достигать) своего локального экстремума внутри этой области. 80. Доказать, что если 81. Доказать, что если 82. Доказать, что если 83. Доказать, что если 84. Пусть граница Г области 85. Пусть Дифференциальные уравнения 86. Найти решение уравнения 87. Проинтегрировать уравнение
88. Найти общее решение уравнения
89. Найти общее решение уравнения
90. Найти общее и особое решение уравнения
91. Найти общее решение следующих уравнений: а) б) в) г) д) 92. Найти общее решение следующих неоднородных дифференциальных уравнений: а) б) в) 93. Пусть в дифференциальном уравнении 94. Доказать, что все решения дифференциального уравнения 95. Доказать, что краевая задача
других решений, кроме 96. Могут ли интегральные кривые данного дифференциального уравнения 97. Сколько существует решений дифференциального уравнения 98. Найти общее решение дифференциальных уравнений в частных производных: а) б) Функциональные уравнения 99. Найдите все нетривиальные функции 100. Найдите все функции 101. Найдите все функции
102. Найдите все непрерывные функции 103. Найдите все функции 104. Найдите все нетривиальные непрерывные функции 105. Найдите все нетривиальные непрерывные функции 106. Найдите все функции и условиям: (Ответ. 107. Найдите все функции
4.2. Задачи для повторения по алгебре и теории чисел
Бинарные отношения
а) Отношение R рефлексивное, так как истинно высказывание: " x Î R (x 2=1Ù x = x). б) Данное бинарное отношение не рефлексивное, так как не для всякого действительного числа его квадрат равен 1. в) Отношение R симметричное, так как истинно высказывание: " x, y Î R ((xy =1Ù x = y)Þ(yx =1Ù y = x)). г) Данное бинарное отношение не симметричное, так как из равенства xy =1 не следует равенство y = x. d) Данное бинарное отношение транзитивно, т.к. истинно высказывание: (" x,y,zÎR) ((xy = 1)Ú(x = y)) Ù ((yz = 1)Ú(y = z)) ® ((xz = 1)Ú(x = z)). е) Данное бинарное отношение не транзитивно, т.к. из равенства xy = 1 и yz = 1 не следует равенство xz = 1. Например, x = ж) Данное бинарное отношение является отношением эквивалентности и разбивает множество R на классы { 0 }, { 1 }, {–1 },...,{ 2, з) Данное бинарное отношение не рефлексивно, не симметрично, не транзитивно. Следовательно, не является отношением эквивалентности. и) График гиперболы
к) График гиперболы
Доказать методом математической индукции:
Комплексные числа
(1+2i)x + (3–5i)y = 1–3i
1)
Системы линейных уравнений
Линейные системы векторов 12. Доказать, что при любых a, b и g система векторов 13. Исследовать, является ли R подпространством векторного пространства C над полем F, если: 1)F = R; 2)F = C; 3)F = Q. 14. Исследовать, является ли линейно зависимой система векторов 15. Исследовать, является ли линейно зависимой система векторов 16. Доказать, что в вещественном пространстве квадратных матрицах второго порядка первый из трех векторов 17. Исследовать, является ли линейно зависимой система векторов 18. Верно ли, что в вещественном пространстве многочленов степени = 2 вектор f(x) = 1 + 4x – 7x2 линейно выражается через векторы f1(x) = 2 – x + x2, и f2(x) = 1 – 2x + 3x2. 19. Подпространство V0 натянуто на систему векторов 20. Решить векторное уравнение:
21. Вычислить ранг матрицы Матрицы и определители 22. Умножить матрицы: 23. Найти 24. Решить матричное уравнение: 1) 25. Вычислить: 26. Вычислить определитель матрицы, разложив по строке или столбцу из букв: 27. Вычислить 28. Решить систему линейных уравнений по правилу Крамера: а)
|
||||||||
|
Последнее изменение этой страницы: 2019-05-20; просмотров: 240; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.21.5 (0.174 с.) |
 , 2)
, 2)  ,
,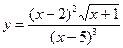 , 4)
, 4)  ,
, , 6)
, 6)  ,
, , 8)
, 8)  ,
, , 10)
, 10)  ,
, , 12)
, 12)  ,
, , 14)
, 14)  ,
, .
. ,
,  и
и  пресекают ось абцисс.
пресекают ось абцисс.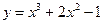 в точке ее пересечения с параболой
в точке ее пересечения с параболой 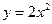 .
. в точке (x 0, y 0) имеет вид
в точке (x 0, y 0) имеет вид  .
. . Определить кинетическую энергию тела через 5 секунд после начала движения.
. Определить кинетическую энергию тела через 5 секунд после начала движения. при x > 1.
при x > 1.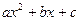 принимает только положительные значения. Доказать, что
принимает только положительные значения. Доказать, что  .
.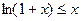 при
при  .
. . (Ответ. 2)
. (Ответ. 2) - нечетная дифференцируемая на R функция. Доказать, что производная
- нечетная дифференцируемая на R функция. Доказать, что производная  - четная функция. Верно ли обратное утверждение?
- четная функция. Верно ли обратное утверждение? - четная дифференцируемая на R функция Доказать, что производная
- четная дифференцируемая на R функция Доказать, что производная  .
.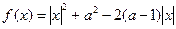 дифференцируема в точке x=0?
дифференцируема в точке x=0? , при этом
, при этом  ,
,  ,
,  положительны на R. Доказать, что существует число
положительны на R. Доказать, что существует число  такое, что
такое, что  при любом
при любом  .
. .
.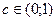 такое, что
такое, что  .
.

 .
. ,
,  .
. имеет хотя бы один корень в интервале (0;1) при любом
имеет хотя бы один корень в интервале (0;1) при любом  .
. такая, что
такая, что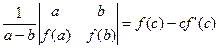 .
. и
и  )
)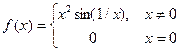 .
. ,
,  .
. .
. , то и
, то и  . Тогда из последнего равенства получим
. Тогда из последнего равенства получим 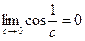 . Но известно, что
. Но известно, что  не существует. Объясните в чем дело?
не существует. Объясните в чем дело? и
и  удовлетворяет неравенству
удовлетворяет неравенству  . Докажите, что
. Докажите, что  .
. , б)
, б)  ,
,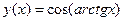 , г)
, г)  .
.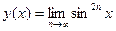
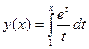 , б)
, б)  .
.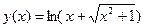 .
. .
.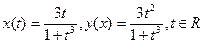
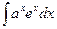 , 2)
, 2) 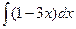 , 3)
, 3) 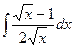 ,
,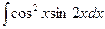 , 5)
, 5)  , 6)
, 6) 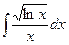 ,
, , 8)
, 8) 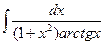 , 9)
, 9) 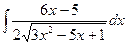 ,
,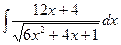 , 11)
, 11)  12)
12)  ,
,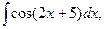 14)
14) 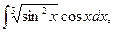 15)
15) 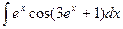
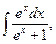 17)
17) 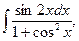 18)
18) 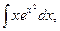

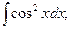 20)
20) 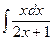 21)
21) 
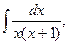 23)
23)  24)
24) 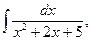
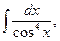 26)
26) 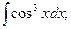 27)
27) 
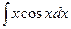 29)
29) 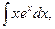 30)
30) 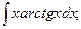
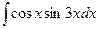 , 32)
, 32)  33)
33) 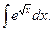
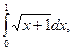 2)
2) 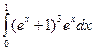 , 3)
, 3) 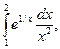
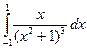 , 5)
, 5) 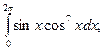 6)
6) 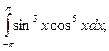
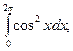 8)
8) 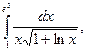 9)
9) 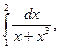
 11)
11)  12)
12) 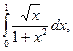
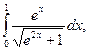 14)
14) 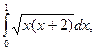 15)
15) 
 17)
17)  18)
18) 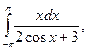
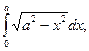 20)
20) 
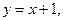
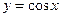 и
и 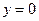 ;
;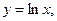
 и
и 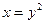 и
и 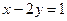 ;
; ;
;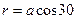 ,
,  .
.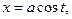
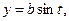
 .
.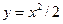 от точки (0;0) до точки (
от точки (0;0) до точки (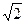 ;1);
;1);
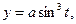
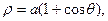
 (кардиоида).
(кардиоида).
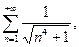 б)
б) 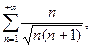 в)
в) 
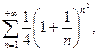 д)
д) 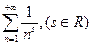 е)
е) 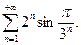
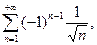 б)
б) 
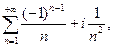 г)
г) 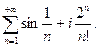
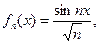 б)
б) 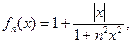
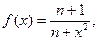 г)
г) 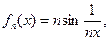
 б)
б) 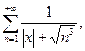
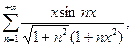 г)
г) 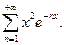
 . Найти область определения этой функции и исследовать ее на непрерывность и дифференцируемость.
. Найти область определения этой функции и исследовать ее на непрерывность и дифференцируемость.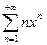 .
.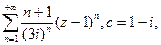 б)
б) 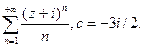
 б)
б) 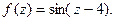
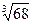 с точностью до 10-3.
с точностью до 10-3.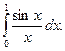
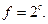
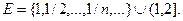 Найти множество предельных, внутренних, граничных, изолированных и внешних точек множества E.
Найти множество предельных, внутренних, граничных, изолированных и внешних точек множества E. где
где 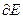 - граница множества
- граница множества 
 - его дополнение до метрического пространства
- его дополнение до метрического пространства 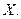
 является одновременно замкнутым и открытым, то
является одновременно замкнутым и открытым, то  либо пусто, либо
либо пусто, либо 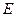 равно
равно 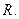
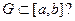
 является гильбертовым.
является гильбертовым.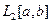 .
.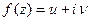 является аналитической в
является аналитической в 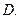 Доказать, что если одна из функций
Доказать, что если одна из функций 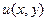 или
или 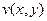 тождественно равна постоянной в
тождественно равна постоянной в  , то и функция
, то и функция 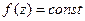 в
в  аналитична в области
аналитична в области 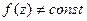 в
в  не может иметь точек локального максимума внутри
не может иметь точек локального максимума внутри 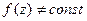 и не имеет нулей в
и не имеет нулей в  , то
, то 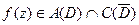 ,
, 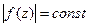 на границе
на границе  , то
, то 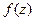 имеет хотя бы один нуль в
имеет хотя бы один нуль в 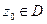 все производные
все производные 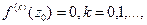 то
то 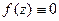 в
в 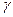 и
и 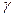 . Доказать, что если
. Доказать, что если 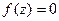 на
на 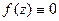 в
в 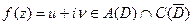 и одна из функций
и одна из функций 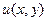 или
или  . Доказать, что
. Доказать, что 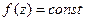 в
в 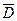 .
.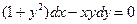 , удовлетворяющее начальному условию
, удовлетворяющее начальному условию 
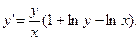
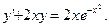

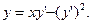




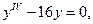

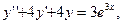



 при всех
при всех 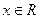 и
и  и
и 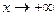 . Доказать, что каждое решение
. Доказать, что каждое решение  такого уравнения стремится к нулю при
такого уравнения стремится к нулю при  ограничены на числовой прямой.
ограничены на числовой прямой.

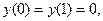
 не имеет.
не имеет. пересекаться в некоторой точке
пересекаться в некоторой точке  плоскости
плоскости 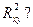
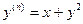 , удовлетворяющих одновременно двум условиям:
, удовлетворяющих одновременно двум условиям: 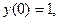
 Рассмотреть отдельно случай
Рассмотреть отдельно случай 



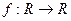 , удовлетворяющие при всех
, удовлетворяющие при всех  и
и  из
из  уравнению
уравнению (Ответ.
(Ответ.  )
) , удовлетворяющие при любых
, удовлетворяющие при любых  (Ответ.
(Ответ. 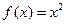 )
) , удовлетворяющие при всех
, удовлетворяющие при всех  (Ответ.
(Ответ.  )
) , удовлетворяющие при всех
, удовлетворяющие при всех 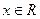 уравнению
уравнению . (Ответ.
. (Ответ.  )
) , уравнению
, уравнению (Ответ.
(Ответ.  )
)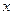 и
и  уравнению
уравнению (Ответ.
(Ответ. 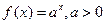 )
)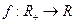 , удовлетворяющие при всех
, удовлетворяющие при всех 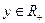 уравнению
уравнению (Ответ.
(Ответ.  )
) удовлетворяющие при всех
удовлетворяющие при всех 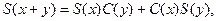




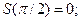 при
при 
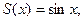
 )
) из класса
из класса  , удовлетворяющие уравнениям:
, удовлетворяющие уравнениям: (Ответ.
(Ответ.  )
) , y = 2, z =
, y = 2, z =  =
=  .
. }, {–a, –
}, {–a, – 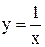 (xy = 1) и точка О(0,0) (т.к. 0 = 0) являются графиком бинарного отношения R
(xy = 1) и точка О(0,0) (т.к. 0 = 0) являются графиком бинарного отношения R

 6, где n Î N, n ³ 1.
6, где n Î N, n ³ 1. .
. . 2)
. 2)  . 3)
. 3)  . 4)
. 4)  . 5)
. 5)  .
. .
. 2)
2) 
 4)
4) 
 6)
6)  .
.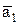 ,
,  ,
,  линейно независима, если
линейно независима, если  =(1, a, b),
=(1, a, b), 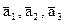 :
: =(1, 2, 1), 2)
=(1, 2, 1), 2) 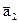 =(1, 1,–1),
=(1, 1,–1),  =(–1,–3,–3).
=(–1,–3,–3).  ,
, 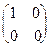 ,
, 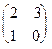 ,
,  не выражается линейно через остальные.
не выражается линейно через остальные. ,
,  , где
, где , где
, где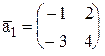 ,
, 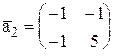 ,
,  ,
, 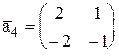




 , если А=
, если А=  А=
А= 
 ×X =
×X =  2)
2) 

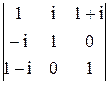


 б)
б) 



