
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Корни многочлена и схема Горнера
55. С помощью схемы Горнера найти неполное частное и остаток от деления f на g, если f=8x8–10x7+36x6–28x5+4x3–24x2+20x+11, g=4x+3. 56. Найти кратность корня c = –2 у многочлена f, если f=x5+6x4+11x3+2x2–12x–8. 57. Разложить f по степеням двучлена x+2, если f=3x5+7x4+x3–2x+3. 58. Записать в стандартном виде многочлен f: f=(x+2)5–3(x–2)3. Полиномы над числовыми полями 59. Доказать неприводимость над Q полинома f: f=x4–2x+3. 60. Разложить многочлен f(x)=x12–2x6+1 на неприводимые множители над полем действительных чисел. 61. Найти многочлен с действительными коэффициентами наименьшей степени, который имеет своими конями числа 2+i, 3 и двукратный корень 1+i. 62. При каком l многочлены f=x3–2lx+l3 и g=x3+l2–2 имеют общий корень в C? Симметрические полиномы 63. Выразить симметрический многочлен через элементарные симметрические многочлены: 1. а) f(x1,x2,x3)=x13+x22+x33+3x1x2x3 б) f(x1,x2,x3)=x12+x22+x32+2x1+2x2+2x3. 64. Многочлен f представить как многочлен от x3 над кольцом R[x1,x2], если f=4x13x2x32+3x1x22x32 – x12x2x33+2x1x22x3 – 3x13x22x3+2x13x33+8x1x3 – 5x1x2+2x3 – 17. Теория делимости 65. Вычислить НОД(588, 2058, 2849) двумя способами. 66. Вычислить НОД(99, 162) и выразить его через данные числа. 67. Доказать, что 8128 - совершенное число. 68. Найти натуральное число, зная, что оно имеет два простых делителя, всего 6 натуральных делителей, сумма которых равна 28. 69. Найти натуральное число, произведение всех натуральных делителей которого равно 5832. 70. Найти количество натуральных чисел, не превосходящих 100 и не делящихся ни на одно из простых чисел: 5, 7, 11. 71. Решить в натуральных числах системы уравнений: а) 72. Построить графики функций: а) y=j (x), б) t=(x), в) s=(x), где x Î N, x³1. Теория сравнений 73. По какому модулю числа 20,–4, 22, 18,–1 составляют полную систему вычетов? 74. Доказать, что система чисел 20, 31,–8, –5, 25, 14, 8,–1, 13, 6 не являются полной системой вычетов по модулю 10. 75. Почему система чисел –5, 13, 11,–25, 5 не является приведенной системой вычетов по модулю 12? 76. Решить сравнения: 77. Вычислить последние две цифры числа 2102. 78. Дробь 79. Представить в виде систематической записи: (51306)7. 80. Перейти к двоичной системе счисления: 1. n=46=(46)10.
81. Перейти к 12-ричной системе счисления: 2. n=19510. 82. Исследовать применяя признаки делимости, делится ли число А на а, если: Основные понятия теории групп 83. Доказать, что множество целых чисел, кратных 3, есть подгруппа аддитивной группы целых чисел. 84. Доказать, что множество матриц вида 85. Исследовать, образует ли группу относительно операции умножения чисел множество М, где М={1,–1, i,–i }, i-мнимая единица. 86. Пусть G- мультипликативная группа невырожденных матриц второго порядка. Найти порядок элемента a1ÎG, если 87. Доказать, что отображение x ® 3x является изоморфизмом аддитивной группы действительных чисел на мультипликативную группу положительных действительных чисел. 88. Доказать, что аддитивную группу всех функций вида ax + b (a, b Î R) можно гомоморфно отобразить на аддитивную группу R, и найти ядро этого гомоморфизма 89. Доказать, что группа <A1, •> изоморфна группе <A2,•>, где 90. Пусть все элементы группы, кроме единицы, имеют порядок 2. Доказать, что группа абелева. Кольца и поля 91. Исследовать, образует ли кольцо относительно операций сложения и умножения матриц множество М матриц вида 92. Исследовать, образует ли кольцо относительно обычных операций сложения и умножения множество Z [i] комплексных чисел вида x+yi, где x,yÎ Z. 93. Пусть на множестве R задано обычное сложение, а умножение Ä: aÄb=b для любых a, bÎ R. Показать, что R не является кольцом относительно (+) и Ä. 94. Пусть
Доказать, что К - кольцо относительно Å и Ä. 95. Исследовать, является ли кольцо К (см. № 80) областью целостности. 96. Пусть а2 = а×а = а для каждого элемента кольца К. Доказать, что кольцо К коммутативно. 97. Составить таблицу Å и Ä элементов колец вычетов а) Z 3, б) Z 8 и выяснить, имеются ли в этих кольцах делители нуля. 98. Доказать, что кольцо <A,+,•> образует поле, если 99. Доказать, что отображение j, такое, что
100. В кольце Z [i] есть 4 обратимых элемента: {–1, 1, i, –i}. Доказать, что других обратимых элементов в кольце Z [i] нет.
4.3. Задачи для повторения по геометрии
Применение векторов к решению геометрических задач. Метода координат на плоскости
Задачи на построение
1. Даны прямая l и точки А, В, лежащие по одну сторону от прямой l. Построить на прямой точку М, для которой длина ломаной AMВ минимальна. 2. В данный остроугольный треугольник АВС вписать треугольник наименьшего периметра так, чтобы его вершины лежали соответственно на сторонах треугольника АВС. Преобразования плоскости 3. Доказать, что если плоская фигура имеет ровно две оси симметрии, то эти оси перпендикулярны. 4. Каким движением является движение, обратное для: а) параллельного переноса Т 5. Пусть f - композиция трех осевых симметрий. Доказать, что f2-параллельный перенос. 6. К какому типу относится движение, отличное от тождественного преобразования и имеющее: а) инвариантную точку и инвариантную прямую, не проходящую через эту точку; б) две пересекающиеся инвариантные прямые? 7. Доказать, что если ограниченная фигура имеет более чем одну ось симметрии, то все эти оси пересекаются в одной точке. 8. Чем является композиция: а) двух параллельных переносов; б) параллельного переноса и осевой симметрии; в) параллельного переноса и центральной симметрии? 9. Доказать, что два прямоугольника равны (т.е. существует движение, переводящее один прямоугольник в другой) тогда и только тогда, когда две смежные стороны одного прямоугольника соответственно равны смежным сторонам другого. 10. Образуют ли коммутативную группу: а) все повороты плоскости; б) все повороты с данным центром 0; в) все параллельные переносы?
11. Доказать, что множество всех параллельных переносов и центральных симметрий образует группу. 12. Доказать, что следующие формулы определяют движение. Найти тип этого движения и элементы, определяющие движение: а) х'= -у-4, у'=х-2; б) х'=-х, у'= у+1; в) х'= х, у' =-у+6. Разложить каждое движение в композицию осевых симметрий. (Записать в определенном порядке уравнения осей). 13. Найти уравнение прообраза, прямой Зх-у+2=0 при параллельном переносе, для которого прямая 2х-у = 0 является инвариантной, а прямая 4х-3 = 0 переходит в прямую 4х-Зу+4 = 0. Какие из данных формул, записанных в прямоугольной декартовой системе координат, являются формулами подобия: а) х'= 3х-4у+8, у'=4х+3у-2; б) х'=8х+у+2, у'=х+8у-3; в) х'=5у+9, у'=5х+20; г) х/=3x+5y+18 у'=5 14. Представить подобие, заданное в прямоугольной декартовой системе координат формулами x' = 4х+2у+5, у'= 2х-4у+3 в виде композиции: а) движения и гомотетии; б) гомотетии и движения. 15. Доказать, что середины сторон треугольника, основания высот и середины отрезов, соединяющих точку пересечения высот с вершинами, лежат на одной окружности (окружность девяти точек). 16. Даны две окружности с центрами 01, 02, касающиеся внешним образом. Доказать, что эти две окружности и окружность, построенная на отрезке 0102 как на диаметре, касаются одной прямой. 17. Доказать, что если в треугольнике две медианы равны, то треугольник равнобедренный. 18. Даны; окружность, прямая и точка А. Построить отрезок с серединой в точке А так, чтобы один его конец лежал на данной окружности, а другой - на данной прямой.
|
||||||||
|
Последнее изменение этой страницы: 2019-05-20; просмотров: 202; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.84.171 (0.024 с.) |

 , б)
, б)  .
. - несократима. Будет ли несократимой дробь
- несократима. Будет ли несократимой дробь  ?
? , где аÎ R \ {0}, есть подгруппа мультипликативной группы G всех невырожденных матриц второго порядка.
, где аÎ R \ {0}, есть подгруппа мультипликативной группы G всех невырожденных матриц второго порядка. .
. 
 , A2=R\{0}.
, A2=R\{0}. , где a, b- любые действительные числа.
, где a, b- любые действительные числа.

 .
.
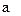
 , является изоморфизмом поля F1 на поле F2, где F1=
, является изоморфизмом поля F1 на поле F2, где F1=  ,F2=Q(
,F2=Q( )=
)=  , а операции определены как обычно.
, а операции определены как обычно. ; б) поворота Rоj; в) симметрии Sl относительно прямой l; г) скользящей симметрии?
; б) поворота Rоj; в) симметрии Sl относительно прямой l; г) скользящей симметрии? х-у+3. Чему равен коэффициент подобия?
х-у+3. Чему равен коэффициент подобия?


