
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Векторные пространства, линейные операторы
29. Найти базис и размерность векторного пространства V над полем R, состоящего из всех матриц вида 30. В двумерном векторном пространстве с базисом "(x, y) ® (3x – 2y, 2x + y), отображение f2 переводит "(x, y) ® (x + y, y). Исследовать, являются ли отображения f1, f2 линейными операторами. Если - да, то вычислить матрицу каждого линейного оператора в базисе 31. Линейный оператор f векторного пространства V над полем R имеет матрицу А,
в некотором базисе 32. Линейный оператор f в базисе
Найти для вектора 33. В трехмерном арифметическом пространстве в базисе
34. В некотором базисе линейный оператор f задан матрицей А, 35. Пусть линейный оператор f задан матрицей А в некотором базисе. Найти собственные векторы и собственные значения линейного оператора f, если
36. В арифметическом пространстве R 4 линейный оператор f в единичном базисе задан матрицей А;
Найти базис ядра линейного оператора f, ранг и дефект f. Полиномы от одной переменной 37. Найти сумму f(x) и g(x), если 38. Найти произведение f·и h, если f=3x4–2x3+2x2+7, h=5x3+4x–5. 39. Найти произведение fg в кольце Z6[x], если f=2x3–3x2–5x+4, g=3x3+5x2–4x+3. 40. Найти необходимое и достаточное условия делимости многочлена f(x) на j(x), если f(x)=x3+2x2+ax–3, j(x)=x2–px+q. 41. Найти частное a и остаток r, если f=2x5+3x4–6x3–5x+7, g=x3+2x2–3x+1, f=g·q+r. 42. Выполнить деление с остатком f на g в кольце многочленов над кольцом классов вычетов Z3[x] по модулю 3, если f=2x4+x+1, g=2x+1. 43. Разложить многочлен f(x)=x12–2x6+1 на неприводимые множители над полем действительных чисел. 44. Найти необходимое и достаточное условия делимости многочлена f(x) на j(x), если f(x)=x3+2x2+ax–3, j(x)=x2–px+q. 45. Выполнить деление с остатком в Q[x] f на g: f=x6–7x5–13x 4+4x2+11x–5, g=x3–5x2+4x–3. 46. Найти необходимые и достаточные условия делимости f на g: f=x3+ax2+3x+c, g=x2+px+2. 47. Найти необходимые и достаточные условия делимости первого многочлена на второй: f=x3+px+q, g=x2+mx–1.
48. Найти остаток от деления f на g, пользуясь схемой Горнера: f=x4–2x3+4x2–6x+8, g=x–1. Наибольший общий делитель и наименьшее общее кратное двух полиномов 49. Найти НОД и НОК: 50. Найти НОД многочленов f(x) и g(x): 51. Для многочленов f=x3–x2+3x–10 и g=x3+6x2–9x–14 найти такие многочлены u и v, что f·u+g·v=d, где d=НОД(f,g). 52. Найти НОД(f,g) и его линейное представление через f и g: f=x3–1, g=x4+x3+2x2+x+1. 53. Найти НОК(f,g): f=x33–1, g=x18–1. 54. Найти НОД и НОК: f=x4–4x3+1, g=x3–3x2+1.
|
|||||
|
Последнее изменение этой страницы: 2019-05-20; просмотров: 192; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.9.115 (0.008 с.) |
 , где a, b, c, dÎ R.
, где a, b, c, dÎ R. ,
,  отображение f1 переводит
отображение f1 переводит ,
,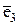 ,
,  . Найти ядро Ker f и дефект f.
. Найти ядро Ker f и дефект f.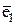 ,
, 
 ,
,  , его образ f(
, его образ f( ,
,  ,
,  линейный оператор f задан матрицей А. Вычислить матрицу С линейного оператора f в базисе
линейный оператор f задан матрицей А. Вычислить матрицу С линейного оператора f в базисе 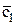 ,
,  ,
,  , если
, если
 . В том же базисе векторы
. В том же базисе векторы  .
. .
.


