Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Множество действительных чисел и его основные свойства.Содержание книги
Поиск на нашем сайте
МИНИСТЕРСТВО НАУКИ И ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ СТЕРЛИТАМАКСКАЯ ГОСУДАРСТВЕННАЯ ПЕДАГОГИЧЕСКАЯ
К.Б. САБИТОВ, П.Н. МИХАЙЛОВ, Р.Х. ВАХИТОВ
Аннотированная программа к государственному экзамену по математике Стерлитамак 2005
Оглавление
§1. Основные требования к знаниям студентов на государственном экзамене по математике §2. Методические рекомендации для подготовки к государственным экзаменам по математике §3. Аннотированные вопросы к государственному экзамену по математике 3.1. Аннотированные вопросы по математическому анализу и дифференциальным уравнениям 3.2. Аннотированные вопросы по алгебре и теории чисел 3.3. Аннотированные вопросы по геометрии §4. Задачи для повторения и подготовки к государственному экзамену по математике 4.1. Задачи для повторенияпо математическому анализу и дифференциальным уравнениям 4.2. Задачи для повторенияпо алгебре и теории чисел 4.3. Задачи для повторенияпо геометрии Рекомендуемая литература
§1. Основные требования к знаниям студентов на государственном экзамене по математике
Основные требования к знаниям студентов на государственном экзамене по математике определены в квалификационной характеристике учителя математики и информатики. Целью государственного экзамена по математике является контроль уровня общей математической культуры выпускников (понимания основных математических понятий, методов и идей, значения математики для практики и развития других наук, умения логически рассуждать и точно формулировать и обосновывать математические утверждения), проверка их подготовленности к преподаванию математике в средней школе. Предполагается, что студенты знакомы с ролью математики и ее важнейших разделов – математического анализа, теории функций и дифференциальных уравнений, алгебры, теории чисел и геометрии – в системе современного научного познания, в технике и в экономике, с основными историческими сведениями и главными направлениями развития математики. Программа ГЭК содержит основные и наиболее важные вопросы, имеющие идейно-теоретическое и практическое значение. В ней также изложены основные требования к знаниям студентов по отдельным разделам математики
Экзаменующиеся должны: v владеть основными понятиями математического анализа, теории функций и дифференциальных уравнений, алгебры, теории чисел и геометрии; v знать главные свойства понятий математического анализа (множество, мощность множества, открытое и замкнутого множество, действительное и комплексное число, функция, последовательность, предел, непрерывность, производная и дифференцируемость, неопределенный и определенный интеграл, сходимость рядов и аналитическая функция), v знать основные элементарные функции и их свойства, метод исследования и построения графиков функций; v уметь вычислять пределы, владеть техникой дифференцирования и интегрирования; v знать начальную задачу для дифференциального уравнения и решать дифференциальные уравнения; v знать основные определения и теоремы линейной алгебры, алгебры многочленов и теории чисел, начальные понятия теории групп, колец и полей; v применять метод математической индукции; v извлекать комплексные корни из комплексных чисел; v решать системы линейных уравнений двумя способами, уметь умножать матрицы и находить обратные матрицы, вычислять определители разными способами; v владеть методом отыскания НОД многочленов при помощи алгоритма Евклида, уметь разлагать многочлен на неприводимые многочлены; v решать уравнения в целых числах; v знать основные определения и теоремы теории делимости в кольце целых чисел и теории сравнений с арифметическими приложениями; v уметь переводить числа из одной позиционной системы в другую, выполнять действия со сравнениями; v знать основные исторические сведения о геометрии; v владеть основными понятиями геометрии (векторы, фигуры, линии и поверхности, проекции, пространства, группы преобразований и многообразия); v знать основные свойства линий и поверхностей в евклидовом пространстве; v применять векторный и координатный методы при изучении геометрии на плоскости и в пространстве; v знать основы теории изображений плоских и пространственных фигур, различные подходы к построению геометрии, основные факты плоскости Лобачевского, определение и примеры топологических многообразий;
v уметь связывать вопросы вузовского и школьного курсов алгебры, геометрии и математического анализа. v владеть логической символикой, основами теории логического вывода.
Оценки «отлично» заслуживает студент, обнаруживший всестороннее, систематическое и глубокое знание учебно-программного материала, умение свободно выполнять задания, предусмотренные программой, усвоивший основную и знакомый с дополнительной литературой, рекомендованной программой. Как правило, оценка «отлично» выставляется студентам, усвоившим взаимосвязь основных понятий дисциплины, их значений для приобретаемой профессии, проявившим творческие способности в понимании учебно-программного материала. Оценки «хорошо» заслуживает студент, обнаруживший полное знание материала, успешно выполняющий предусмотренные в программе задания, усвоивший основную литературу. Как правило, оценка «хорошо» выставляется студентам, показавшим систематический характер знаний по дисциплине и способным к их самостоятельному пополнению и обновлению в ходе дальнейшей учебной работы и профессиональной деятельности. Оценки «удовлетворительно» заслуживает студент, обнаруживший знание основного учебно-программного материала в объеме необходимом для дальнейшей учебы и предстоящей работы по профессии, справляющийся с выполнением заданий, предусмотренных программой, знакомый с основной литературой. Как правило, оценка «удовлетворительно» выставляется студентам, допустившим погрешности в ответе и при выполнении экзаменационных заданий, но обладающим необходимыми знаниями для их устранения под руководством преподавателя. Оценки «неудовлетворительно» выставляется студенту, обнаружившему пробелы в знаниях основного учебно-программного материала, допустившему принципиальные ошибки в выполнении предусмотренных программой заданий. Как правило, оценка «неудовлетворительно» ставится студентам, которые не могут продолжить обучение или приступить к профессиональной деятельности по окончании ВУЗ без дополнительных занятий по соответствующей дисциплине.
§2. Методические рекомендации для подготовки к государственным экзаменам по математике
Основными критериями при оценке ответа экзаменующегося на государственном экзамене по математике является его научная обоснованность, полнота, общность, связь со школьной математикой. Отличительной особенностью ответа на государственных экзаменах является обзорность, ибо на подробное изложение всех вопросов просто нет времени, но экзаменующийся должен быть готов при необходимости (по требованию комиссии) привести и соответствующие доказательства сформулированных утверждений. При подготовке к государственному экзамену по математике основными пособиями служат литература, указанная в конце данного пособия, и конспекты лекций по математическому анализу, теории функций и дифференциальным уравнениям, алгебре, теории чисел и геометрии. По программе государственных экзаменов читаются специальные курсы «Избранные вопросы математики» (по математическому анализу, алгебре и геометрии), цель которых глубокое осмысление и систематизация полученных в течение пяти лет обучения знаний и их связей со школьным курсом математики. В этих курсах читаются обзорные лекции, которые представляют собой не просто повторное чтение тех или иных разделов, а дают лишь примерную схему изложения соответствующего вопроса, при этом заостряется внимание студента на идейных основных моментах. На основе обзорных лекций рекомендуется составить полный ответ на каждый вопрос, отметив для себя, какие теоремы, факты будут доказаны, а какие просто сформулированы с приведением идеи доказательства.
При подготовке ответа во время экзамена следует составить план своего ответа, используя данное пособие, в котором указывается объем и содержание вопросов, выносимых на государственный экзамен. Записи на доске должны быть аккуратными, лаконичными. Следует приводить лишь основные формулы, особо важные выкладки. При ответе следует рассказать основные утверждения и их доказательства, не затушевывая второстепенными деталями, иллюстрировать рассматриваемые понятия и факты примерами.
§3. Аннотированные вопросы к государственному экзамену по математике
3.1. Аннотированные вопросы по математическому анализу и дифференциальным уравнениям
Квадрируемые фигуры. Приложение определенного интеграла к вычислению площади плоской фигуры. Квадрируемые фигуры. Необходимое и достаточное условие квадрируемости фигуры. Необходимое и достаточное условие квадрируемости фигуры. В терминах меры границы этой фигуры. Достаточное условие квадрируемости фигуры, ограниченной графиками нескольких непрерывных функций. Квадрируемость фигуры в терминах предела последовательности площадей квадрируемых фигур. Свойства квадрируемых фигур (инвариантность, аддитивность и монотонность) (обзорно). Площадь криволинейной трапеции. Площадь криволинейного сектора в полярной системе координат. Примеры. Группа. Примеры групп. Простейшие свойства группы. Подгруппа. Гомоморфизм и изоморфизм групп. Определение группы. Аддитивная и мультипликативная теоретико-групповая терминология. Примеры групп (числовые группы, группы классов вычетов, матричные группы, группы подстановок). Простейшие свойства группы (разрешимость уравнений вида ax = b и ya = b; правила сокращений; элементы, симметричные нейтральному элементу, симметричному элементу и произведению двух элементов). Определение и примеры подгруппы и гомоморфизма и изоморфизма групп. Кольцо. Примеры колец. Простейшие свойства кольца. Подкольцо. Гомоморфизм и изоморфизм колец. Определение кольца, ассоциативного и коммутативного кольца и кольца с единицей. Примеры ассоциативных колец (числовые кольца, матричные кольца, кольца функций и кольца многочленов). Простейшие свойства кольца (умножение на нуль, правила знаков, дистрибутивность умножения относительно вычитания). Кольца без делителей нуля. Примеры колец с делителями нуля. Определение и примеры подкольца и гомоморфизма и изоморфизма колец.
Система натуральных чисел как некоторая алгебраическая система, удовлетворяющая аксиомам Пеона. Аксиома математической индукции. Принцип математической индукции. Метод математической индукции (способ доказательства теорем, опирающийся на принцип математической индукции): базис индукции, индукционный шаг, индуктивное предположение. Примеры доказательства методом математической индукции (сумма первых n членов арифметической прогрессии, число подмножеств множества, состоящего из n элементов и т.п.). Поле. Простейшие свойства поля. Примеры полей. Поле рациональных чисел. Упорядоченное поле. Определение и простейшие свойства поля (аддитивная и мультипликативная группы поля, кольцевые свойства, отсутствие делителей нуля). Характеристика поля: 0 или простое число. Примеры конечных полей: кольца вычетов по простому модулю. Примеры бесконечных полей: числовые поля Q, R, C и др. Поле рациональных чисел как наименьшее поле нулевой характеристики. Определение линейно упорядоченного поля. Предложение: поле комплексных чисел линейно не упорядочивается. Векторное пространство. Примеры и простейшие свойства векторных пространств. Линейная зависимость и независимость системы векторов. Базис и ранг конечной системы векторов. Определение и простейшие свойства векторного пространства над полем. Арифметическое векторное пространство. Определение и простейшие свойства линейной зависимости и независимости системы векторов. Эквивалентные системы векторов. Базис системы векторов. Теорема о существовании базиса и о числе элементов базисов. Ранг системы векторов. Приложение теории сравнений к выводу признаков делимости. Признак делимости на степени 2 и 5. Признаки делимости на число, взаимно простое с10: по сумме и по знакочередующейся сумме граней с числом цифр, равным первообразному корню. Группа движений плоскости. Определение движений плоскости. Примеры движений. Задание движений с помощью пары ортонормированных реперов. Свойства движений. Группа движений и ее инварианты. Понятие равенства фигур. Теоретико-групповой подход в геометрии. Применение движений к решению задач. Плоскость Лобачевского. Исторические сведения о возникновении геометрии Лобачевского. Система аксиом геометрии Лобачевского. Непротиворечивость и полнота системы аксиом. Примеры доказательств некоторых теорем плоскости Лобачевского. Функция
а) б) в) д) 2. Построить график функций: а) б) в) д) 3. Доказать, что функция 4. Найти период функции:
а) 5. Доказать, что функция Дирихле имеет своим периодом любое рациональное число 6. Найти наименьшее или наибольшее значение функции и построить график: а) в) Предел функции и последовательности 7. Вычислить предел функции: 1) 3) 5) 7) 9) 11) 13) 15) 17) 19) 8. Найти предел последовательности: а) в) 9. Пусть x 1 > 0, (Ответ. 1) 10. Пусть (Ответ. 2) 11. Найти предел (Ответ. 12. Найти предел (Ответ. 2 (Указание. Использовать формулу Тейлора для функции 13. Найти предел (Ответ. 1) 14. Доказать, что а) 15. Доказать, что если
16. Доказать, что если Непрерывность функции 17. Исследовать на непрерывность, построить график функции: а)
б) в) г) 18. Пусть функция 19. Пусть функции 20. Доказать, что если функция непрерывна на отрезке и имеет обратную функцию, то она монотонна на этом отрезке. 21. Пусть 22. Пусть 23. Пусть 24. Пусть функция График функции Построить график следующих функций 45. а) в) 46. 47. а) 48. 49. 50. Интегрирование 51. Вычислить неопределенный интеграл: 1) 4) 7) 10) 13) 16) 19) 22) 25) 28) 31) 52. Вычислить определенный интеграл: 1) 4) 7) 10) 13) 16) 19) 53. а) Вычислить площадь фигуры ограниченной линиями: 1) 2) 3) 4) 5) б) Найти площадь фигуры, ограниченной эллипсом; в) Найти длину кривой: 1) 2) 3) Ряды 54. Найти сумму ряда 55. Исследовать на сходимость: а) г) 56. Исследовать на абсолютную или условную сходимость: а) в) 57. Исследовать на равномерную сходимость функциональные последовательности: а) в) 58. Исследовать на равномерную сходимость функциональные ряды: а) в) 59. Пусть задана функция 60. Найти сумму степенного ряда 61. Найти круг сходимости степенного ряда. Будет ли аналитической его сумма в точке с? а) 62. Разложить функцию в ряд Тейлора в окрестности точки z0=2 и найти круг сходимости: а) 63. Вычислить приближенно число 64. Вычислить с точностью до 10-3 интеграл Теория функций 65. Установить биекцию между сегментом [0;1] и интервалом (0,1). 66. Доказать, что множество всех функций, непрерывных на [ а, b ], имеет мощность континуума. 67. Доказать, что множество всех функций (непрерывных и разрывных), заданных на сегменте [ a, b ], имеет мощность f, большую, чем мощность континуума, причем 68. Доказать, что множество всех точек разрыва монотонной функции, заданной на промежутке < a, b > не более чем счетно. 69. Дано множество 70. Доказать, что замыкание любого множества замкнуто. 71. Доказать, что множество замкнуто тогда и только, когда оно совпадает со своим замыканием. 72. Доказать, что граница любого множества замкнута, причем 73. Доказать, что если множество 74. Доказать, что расстояние между непересекающимися замкнутыми множествами строго положительно, если хотя бы одно из этих множеств ограничено. 75. Может ли быть интегрируемой по Риману на [ a, b ] функция, разрывная во всех точках некоторого непустого открытого множества 76. Доказать, что пространство 77. Доказать, что множество непрерывных функций, заданных на [ a, b ], всюду плотно в 78. Пусть функция 79. Доказать, что функция гармоничная в некоторой области и отличная от постоянной не может принимать (достигать) своего локального экстремума внутри этой области. 80. Доказать, что если 81. Доказать, что если 82. Доказать, что если 83. Доказать, что если 84. Пусть граница Г области 85. Пусть Дифференциальные уравнения 86. Найти решение уравнения 87. Проинтегрировать уравнение
88. Найти общее решение уравнения
89. Найти общее решение уравнения
|
|||||||||
|
Последнее изменение этой страницы: 2019-05-20; просмотров: 188; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.146.221.131 (0.016 с.) |

 ,
,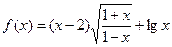
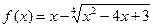 , г)
, г) 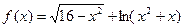 ,
,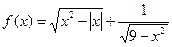 .
.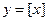 - целая часть числа
- целая часть числа 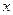 ;
;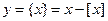 - дробная часть числа
- дробная часть числа  , г)
, г)  ,
, , е)
, е)  .
.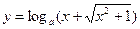 является нечетной.
является нечетной. , в)
, в) 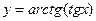 .
.
 .
. , б)
, б)  ,
, , г)
, г) 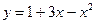 .
.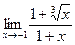 , 2)
, 2) 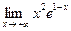 ,
,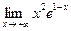 , 4)
, 4)  ,
,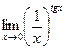 , 6)
, 6)  ,
, , 8)
, 8)  ,
,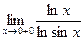 , 10)
, 10) 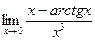 ,
, , 12)
, 12) 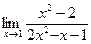 ,
,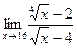 , 14)
, 14) 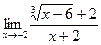 ,
, , 16)
, 16) 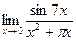 ,
,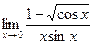 , 18)
, 18) 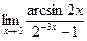 ,
,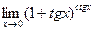 , 20)
, 20) 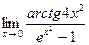 .
.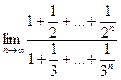 , б)
, б) 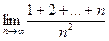 ,
,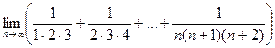 .
.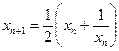 при
при 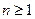 . Доказать, что существует предел
. Доказать, что существует предел  и найти его.
и найти его.  ,
, 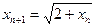 . Доказать, что последовательность (xn) имеет предел и найти его.
. Доказать, что последовательность (xn) имеет предел и найти его. .
. )
)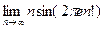 .
.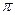 )
) при x =1)
при x =1) .
.  , (а > 0), б)
, (а > 0), б) 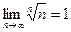
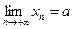 , то
, то .
.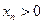 при всех
при всех  и
и 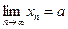 , то
, то 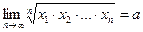 .
.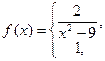
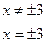 ,
,
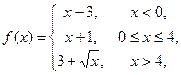

 и строго монотонна на
и строго монотонна на 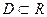 . Доказать, что если точка x 0 является предельной точкой множества D, то
. Доказать, что если точка x 0 является предельной точкой множества D, то 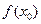 есть предельная точка множества
есть предельная точка множества 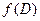 .
.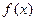 и
и 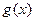 непрерывны на интервале (a, b) и одна из них монотонна. Пусть некоторая последовательность (xn) точек [ a, b ] удовлетворяет условию
непрерывны на интервале (a, b) и одна из них монотонна. Пусть некоторая последовательность (xn) точек [ a, b ] удовлетворяет условию 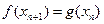 при всех
при всех  . Доказать, что если последовательность (xn) сходится, то уравнение
. Доказать, что если последовательность (xn) сходится, то уравнение  имеет решение.
имеет решение.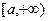 и существует конечный предел
и существует конечный предел  . Доказать, что
. Доказать, что  и
и  . Доказать, что функция
. Доказать, что функция 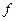 ограничена снизу и принимает свое наименьшее значение.
ограничена снизу и принимает свое наименьшее значение. периодическая функция. Доказать, что если существует предел
периодическая функция. Доказать, что если существует предел  , то
, то 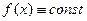 .
.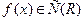 . Доказать, что если
. Доказать, что если 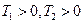 таких, что отношение
таких, что отношение 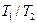 иррационально, то
иррационально, то 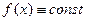 .
. , б)
, б)  ,
,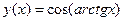 , г)
, г)  .
.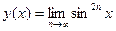
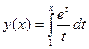 , б)
, б)  .
.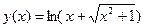 .
. .
.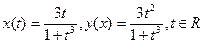
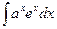 , 2)
, 2) 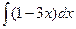 , 3)
, 3) 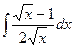 ,
,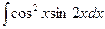 , 5)
, 5)  , 6)
, 6) 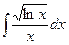 ,
, , 8)
, 8) 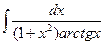 , 9)
, 9) 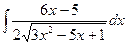 ,
,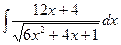 , 11)
, 11)  12)
12)  ,
,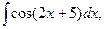 14)
14) 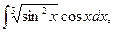 15)
15) 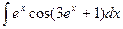
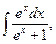 17)
17) 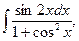 18)
18) 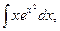

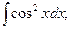 20)
20) 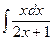 21)
21) 
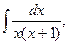 23)
23)  24)
24) 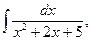
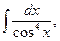 26)
26) 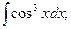 27)
27) 
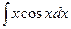 29)
29) 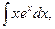 30)
30) 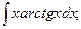
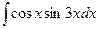 , 32)
, 32)  33)
33) 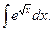
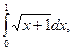 2)
2) 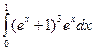 , 3)
, 3) 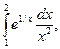
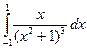 , 5)
, 5) 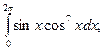 6)
6) 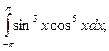
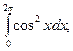 8)
8) 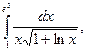 9)
9) 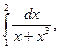
 11)
11)  12)
12) 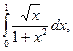
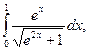 14)
14) 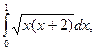 15)
15) 
 17)
17)  18)
18) 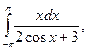
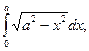 20)
20) 
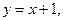
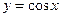 и
и 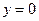 ;
;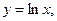
 и
и 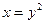 и
и 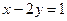 ;
; ;
;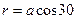 ,
,  .
.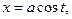
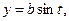
 .
.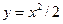 от точки (0;0) до точки (
от точки (0;0) до точки (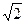 ;1);
;1);
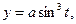
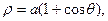
 (кардиоида).
(кардиоида).
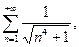 б)
б) 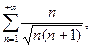 в)
в) 
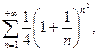 д)
д) 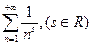 е)
е) 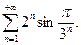
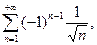 б)
б) 
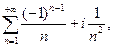 г)
г) 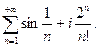
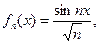 б)
б) 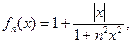
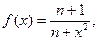 г)
г) 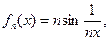
 б)
б) 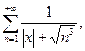
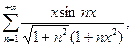 г)
г) 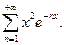
 . Найти область определения этой функции и исследовать ее на непрерывность и дифференцируемость.
. Найти область определения этой функции и исследовать ее на непрерывность и дифференцируемость.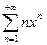 .
.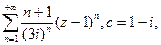 б)
б) 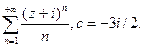
 б)
б) 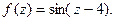
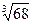 с точностью до 10-3.
с точностью до 10-3.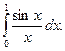
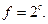
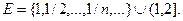 Найти множество предельных, внутренних, граничных, изолированных и внешних точек множества E.
Найти множество предельных, внутренних, граничных, изолированных и внешних точек множества E. где
где 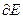 - граница множества
- граница множества 
 - его дополнение до метрического пространства
- его дополнение до метрического пространства 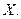
 является одновременно замкнутым и открытым, то
является одновременно замкнутым и открытым, то  либо пусто, либо
либо пусто, либо 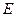 равно
равно 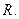
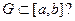
 является гильбертовым.
является гильбертовым.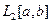 .
.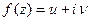 является аналитической в
является аналитической в 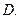 Доказать, что если одна из функций
Доказать, что если одна из функций 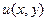 или
или 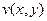 тождественно равна постоянной в
тождественно равна постоянной в  , то и функция
, то и функция 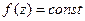 в
в  аналитична в области
аналитична в области 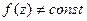 в
в  не может иметь точек локального максимума внутри
не может иметь точек локального максимума внутри 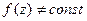 и не имеет нулей в
и не имеет нулей в  , то
, то 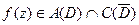 ,
, 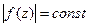 на границе
на границе  , то
, то 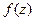 имеет хотя бы один нуль в
имеет хотя бы один нуль в 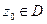 все производные
все производные 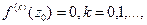 то
то 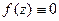 в
в 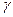 и
и 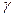 . Доказать, что если
. Доказать, что если 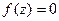 на
на 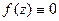 в
в 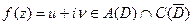 и одна из функций
и одна из функций 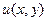 или
или  . Доказать, что
. Доказать, что 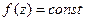 в
в 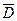 .
.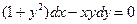 , удовлетворяющее начальному условию
, удовлетворяющее начальному условию