
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод координат в пространстве
19. Написать уравнение плоскости, которая: а) параллельна координатной плоскости ОXY и проходит через точку А(2, -5, 3), б) содержит ось аппликат и точку В(-3, 1, -2), в) параллельна оси абсцисс и проходит через точки С(4, 0, -2) и D(5, 1, 7). Система координат - аффинная. 20. Написать параметрические уравнения плоскости, которая проходит через точку А(2,-1,3) параллельно плоскости, заданной уравнением 2х-y+3z-l=0. Перейти от полученных параметрических уравнений к общему уравнению плоскости. Система координат - аффинная. 21. Написать уравнения прямой: а) проходящей через точку А(2,1,-3) и параллельной вектору 22. Определить взаимное расположение двух прямых, заданных в аффинной системе координат уравнениями: a) x=l+2t, y=7+t, z=3+4t; x=6+3t, y=-l-2t,z=-2+t; б)x=-2+3t, y=-l, z=4-t; 2x-z+2=0, x-7y+3z-17=0 в) x-y-z=0, 2x-y+2z=0; х/1=(у+8)/(-4)=(z+3)/(-3). 23. Написать уравнения прямой, проходящей через точку А(2,3,1) и пересекающей прямые, заданные в аффинной системе координат уравнениями x+y=0, х+Зу-1= 0, x-y+z+4=0; y+z-2=0. 24. Найти уравнения ортогональной проекции прямой d, заданной системой уравнений 5х+8у-3z +9=0 и 2х-4у+ z-1=0, на координатную плоскость Оху и величину угла, который прямая d образует с этой плоскостью. 25. Написать уравнения прямой, которая проходит через точку Р(2,-1,0) и пересекает под прямым углом прямую, заданную уравнениями: x/1=(y+1)/(-3)=(z+1)/(-2). 26. Найти точку, симметричную точке М(2,7,1) относительно плоскости, заданной уравнением х-4у+ z +7=0. 27. Написать уравнения прямой, содержащей общий перпендикуляр оси ординат и прямой, заданной уравнениями: x=3+4t, y=l-t, z =2+5t. 28. Найти расстояние между прямыми l 1: x=2+4t, y=-l+t, z=1-t и l 2: (x+4)/2 = (y-2)/(-2) =(z+2)/(-3). 29. На оси аппликат найти точку, которая удалена от плоcкости x+2y-2z -2 =0 на расстояние r =4. 30. Даны плоскости 3х+5у-4 z +1=0 и х-z-5=0. Найти угол между этими плоскостями и написать уравнение биссекторной плоскости того угла между ними, в котором лежит начало координат. 31. Найти множество всех точек пространства, каждая из которых равноудалена от трех попарно не параллельных плоскостей.
32. Написать уравнение плоскости, проходящей через линию пересечения плоскостей, заданных уравнениями x+y-z+l=0 и 2х+3у-z+2=0,и перпендикулярной к плоскости, заданной уравнением х-у+2z -1=0. 33. Написать уравнения прямой, содержащей общий перпендикуляр двух прямых, заданных уравнениями (х-1)/2 = - (y-l)/1 = (z-3)/4 и (х- 6)/3 = - (у+1)/2 = - (z +2)/1. Проективная геометрия 34. Пусть F22— двумерное векторное пространство над полем F2, вычетов по модулю 2. Доказать, что проективная прямая Р(F22) содержит точно три точки. 35. Доказать, что проективная плоскость содержит по крайней мере 7 точек. 36. Сколько прямых содержит проективная плоскость Р(F32)? 37. На модели проективной прямой P1(R) (в пучке прямых Р (О) или на расширенной прямой d) задан проективный репер (А0,А1,Е). Построить точки М(1, -1), N (-2, 1), L (-2, 2) по их координатам в этом репере. 38. На чертеже ограниченных размеров заданы точка А и пара прямых р и q, пересекающихся за пределами чертежа в точке В (недоступной точке). Воспользовавшись теоремой Дезарга, построить доступную часть прямой (АВ). 39. На чертеже ограниченных размеров заданы две пары прямых: р, q, пересекающиеся в недоступной точке А, и 40. С помощью одной линейки через данную точку А провести прямую, параллельную двум заданным параллельным прямым р и q (р 41. Вычислить сложное отношение четырех точек А(1,0,1); В(1,1,3); С(2,1,4); Д(0,1,2) по их проективным координатам на плоскости. 42. На аффинной (или евклидовой) плоскости П даны отрезок [АВ] и его середина С. Через данную точку М 43. Даны две параллельные прямые (различные). Пользуясь только линейкой, построить: 1) середину отрезка, заданного на одной из данных прямых; 2) прямую, проходящую через данную точку и параллельную данным прямым. 44. Выяснить тип инволюции: 45. Вычислить координаты неподвижных точек проективного преобразования плоскости: 46. Пусть на проективной плоскости заданы две различные прямые: а: а
Изображение фигур в параллельной проекции 47. Построить изображения квадрата, куба, правильной восьмиугольной пирамиды в параллельной проекции. 48. Какая фигура может служить изображением в параллельной проекции равнобочной трапеции, длины оснований которой относятся как 2:3. 49. Дано изображение окружности в параллельной проекции. Построить изображения: 1) вписанного в нее правильного треугольника; 2) описанного около нее правильного треугольника. 50. Через данную точку провести касательную к данному эллипсу. 51. Дано изображение окружности в параллельной проекции. Построить изображение вписанного в нее правильного шестиугольника. 52. Построить изображение цилиндра, описанного около шара. 53. Построить изображение правильной треугольной призмы, описанной около шара. 54. В параллельной проекции даны изображения окружности и угла, лежащего в плоскости окружности. Построить изображение его биссектрисы. 55. В параллельной проекции дано изображение треугольника, вписанного в окружность. Построить изображение центра окружности, вписанной в этот треугольник. 56. В параллельной проекции дано изображение треугольника, вписанного в окружность. Построить изображения его высот. Основания геометрии 57. На конечном множестве построить интерпретацию 1 группы аксиом Гильберта. 58. Пользуясь только аксиомами 1 группы Гильберта, доказать, что каждой плоскости принадлежат по крайней мере три точки, не лежащие на одной прямой. 59. Пользуясь только аксиомами 1 и II групп Гильберта, доказать, что множество внутренних точек отрезка не пусто. 60. Построить интерпретацию 1 группы аксиом школьного курса геометрии на конечном множестве. 61. Пользуясь аксиомами школьного курса геометрии, доказать, что: 1) каждый отрезок содержит бесконечное множество точек; 2) каждая плоскость содержит бесконечное множество точек, не лежащих на одной прямой; 3) пространство содержит бесконечное множество точек, не лежащих на одной плоскости. 62. Пользуясь аксиомами школьного курса геометрии, доказать, что: 1) сумма величин внутренних углов любого треугольника равна
|
||||||
|
Последнее изменение этой страницы: 2019-05-20; просмотров: 388; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.33.175 (0.01 с.) |
 ;б) проходящей через точки А(2, -3, 1/2) и В(3, 5, 3/2); в) образованной пересечением плоскости х+3у-z+1=0 с плоскостью OXY; г) проходящей через точку А(1, -3, 4) параллельно прямой, заданной системой уравнений 2x-y+z-3=0, x+3y-z-1=0. д) проходящей через точку А(0, 0, 2) и перпендикулярной прямым, заданным уравнениям: х =1+t, y=l-t, z=t; x=l-t, y=2, z=3-t. В случаях а) - г) система координат аффинная, в случае д) – прямоугольно декартова.
;б) проходящей через точки А(2, -3, 1/2) и В(3, 5, 3/2); в) образованной пересечением плоскости х+3у-z+1=0 с плоскостью OXY; г) проходящей через точку А(1, -3, 4) параллельно прямой, заданной системой уравнений 2x-y+z-3=0, x+3y-z-1=0. д) проходящей через точку А(0, 0, 2) и перпендикулярной прямым, заданным уравнениям: х =1+t, y=l-t, z=t; x=l-t, y=2, z=3-t. В случаях а) - г) система координат аффинная, в случае д) – прямоугольно декартова. u,v, пересекающиеся в недоступной точке В. Построить доступную часть прямой (АВ).
u,v, пересекающиеся в недоступной точке В. Построить доступную часть прямой (АВ). q).
q). (АВ) провести прямую, параллельную прямой (АВ), пользуясь только линейкой.
(АВ) провести прямую, параллельную прямой (АВ), пользуясь только линейкой. у0=х0-2х1,
у0=х0-2х1, 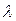 у0=х0,
у0=х0, 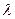 у2=х1+х2.
у2=х1+х2. х
х  х
х  = 0 (а= 0, 1, 2) своими уравнениями относительно проективного репера R. Доказать, что уравнение:
= 0 (а= 0, 1, 2) своими уравнениями относительно проективного репера R. Доказать, что уравнение: 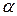 х
х  +
+  в
в  принимают вещественные значения, не равные нулю одновременно, определяет пучок прямых на проективной плоскости.
принимают вещественные значения, не равные нулю одновременно, определяет пучок прямых на проективной плоскости.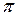 ;3) около всякого треугольника можно описать окружность.
;3) около всякого треугольника можно описать окружность.


