
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теплопроводность при стационарном режиме в однослойной и многослойной стенках различной конфигурации.Содержание книги
Поиск на нашем сайте
Однородная цилиндрическая стенка Задача о распространении тепла в цилиндрической стенке также одномерная, если ее рассматривать в цилиндрических координатах. температура изменяется только вдоль радиуса r, а по длине и по ее периметру остается неизменной. В соответствии с законом Фурье, тепловой поток через однородную цилиндрическую стенку длиной l определяется по формуле:
При значениях d2/d1 близких к единице расчеты Rl
где dcp=0,5(d1+d2) - средний диаметр трубы. В толще однородной цилиндрической стенки температура изменяется по логарифмическому закону. Многослойная цилиндрическая стенка Аналогично многослойной плоской стенке, полное термическое сопротивление многослойной цилиндрической стенки можно записать:
где di и di+1 - соответственно внутренний и внешний диаметры iго слоя. Тогда линейная плотность теплового потока будет:
Для многослойной цилиндрической стенки распределение температур - ломаная логарифмическая линия. Задачи 1. Определить тепловой поток через бетонную стену здания толщиной 200 мм, высотой 2,5 м и длиной 2 м, если температуры на ее поверхностях tc1=20°С, tc2= -10°С, а коэффициент теплопроводности 2. Определить коэффициент теплопроводности материала стенки толщиной 50 мм, если плотность теплового потока через нее 100 Вт/м2, а разность температур на поверхностях 3. Плоскую поверхность необходимо изолировать так, чтобы потери теплоты с единицы поверхности в единицу времени не превышали 450 Вт/м2. Температура поверхности под изоляцией tc1=450°С, температура внешней поверхности изоляции tc2=50°С. определить толщину изоляции, выполненной из совелита, для которого 4. Распределение температуры по толщине плоской стенки с 5. Плотность теплового потока через плоскую стенку толщиной 50 мм q=70 Вт/м2. Определить разность температур на поверхностях стенки и численное значение градиента температуры в стенке, если она выполнена: а) из латуни [ 6. Плоская стенка бака площадью 5 м2 покрыта двухслойной тепловой изоляцией. Стенка бака стальная, толщиной d1=8мм с коэффициентом теплопроводности 7. Стены сушильной камеры выполнены из слоя красного кирпича толщиной d1=250мм [l1=0,7 Вт/(м×К)] из слоя строительного войлока [l2=0,0465 Вт/(м×К)]. Вычислить температуру в плоскости соприкосновения слоев и толщину войлочного слоя при условии, что тепловые потери ровны 0. 8. Стенка неэкранированной топочной камеры парового котла выполнена из слоя пеношамота (l1=0,28+0,00023×t) толщиной d1=125мм и слоя красного кирпича (l2=0,7 Вт/(м×К)) толщиной d2=500мм. Слои плотно прилегают друг к другу. Температура на внутренней поверхности топочной камеры tc1=1100°С, а на наружной tc3=50°С. Вычислить плотность теплового потока и температуру в плоскости соприкосновения слоев. 9. Нефтепровод с наружным диаметром 1220мм и толщиной стенки dтр=10мм [lтр=55 Вт/(м×К)] имеет три слоя изоляции толщиной d1=8мм, d2=12мм, d3=25мм. Коэффициенты теплопроводности изоляции l1=0,0035Вт/(м×К), l2=0,06Вт/(м×К), l3=0,12 Вт/(м×К). температура на внутренней поверхности трубы tвн=60°С, а на наружной поверхности изоляции tнар= -5°С. Определить линейную плотность теплового потока. 10. Железебетонная дымовая труба [l2=1.1 Вт/(м×К)] внутренним диаметром d2=800мм и наружным диаметром d3=1300мм должна быть футерована внутри огнеупором [l1=0,5 Вт/(м×К)]. Определить толщину футеровки и температуру наружной поверхности трубы tс3 из условий, чтобы тепловые потери с 1м трубы не превышали 2000 Вт/м, а температура внутренней поверхности железобетонной стенки tс2 не превышала 200°С. Температура внутренней поверхности футеровки tс1=425°С. 11. В приборе для определения коэффициента теплопроводности жидкостей по методу «нагретой нити» в кольцевой зазор между платиновой нитью и кварцевой трубкой залито испытуемое трансформаторное масло. Диаметр и длина платиновой нити d1=0,12мм и l=90мм; внутренний и наружный диаметры кварцевой трубки d2=1мм, d3=3мм, коэффициент теплопроводности кварца lкв=1,4 Вт/(м×К). Вычислить коэффициент теплопроводности и среднюю температуру трансформаторного масла, если при расходе теплоты через кольцевой слой масла Q=1,8Вт, температура платиновой нити tс1=106,9°С и температура внешней поверхности кварцевой трубки tс3=30,6°С.
ЛЕКЦИя 12 Раздел 9. Теплопередача
В технике часто приходится рассчитывать стационарный процесс переноса теплоты от одного теплоносителя другому через разделяющую стенку. Такой процесс называется теплопередачей.
Плоская стенка Рассмотрим теплопередачу между двумя жидкостями через разделяющую из многослойную плоскую стенку. Здесь передача теплоты делится на три процесса: 1) В начале теплота передается от горячего теплоносителя tж1 к поверхности стенки путем конвективного теплообмена, который может сопровождаться излучением. Интенсивность процесса теплоотдачи характеризуется коэффициентом теплоотдачи a1.
 
При стационарном режиме плотность теплового потока во всех трех процессах одинакова и может быть записана следующим образом: 1. по закону Ньютона - Рихмана
2. по закону Фурье
3. по закону Ньютона - Рихмана
где Из вышеприведенных уравнений составив систему уравнений:
и сложив правые и левые части, получим уравнения теплопередачи через многослойную плоскую стенку:
или
где Rk - термическое сопротивление теплопередачи от горячего теплоносителя к холодному. Величина, обратная Rk, называется коэффициентом теплопередачи К:
Коэффициент теплопередачи К характеризует интенсивность процесса теплопередачи от горячего теплоносителя к холодному через разделяющую их стенку. Тогда уравнение теплопередачи можно записать:
Граничные температуры определяются из (3.4):
Очевидно, что для однослойной плоской стенки формулы справедливы, где
Цилиндрическая стенка Рассмотрим теплопередачу между двумя жидкостями через разделяющую их многослойную цилиндрическую стенку. аналогично теплопередаче через плоскую стенку, линейную плотность теплового потока через многослойную цилиндрическую стенку при стационарном режиме можно записать: 1. по закону Ньютона - Рихмана
2. по закону Фурье
3. по закону Ньютона - Рихмана
где Аналогично получим линейную плотность теплового потока:
где Rlk - линейное термическое сопротивление, (м×К)/Вт. Kl - линейный коэффициент теплопередачи, Вт/(м×К)
Граничные температуры цилиндрической стенки определяются как
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 791; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.98.39 (0.007 с.) |

 ,
,










 ,
, - линейное термическое сопротивление теплопроводности трубы.
- линейное термическое сопротивление теплопроводности трубы. должны производиться с высокой точностью, т.к. при округлении d2/d до одного знака после запятой погрешность вычисления логарифма будет больше 10%. С точностью до 4% при d2/d1 < 2 в практических расчетах рекомендуется пользоваться формулой для плоской стенки:
должны производиться с высокой точностью, т.к. при округлении d2/d до одного знака после запятой погрешность вычисления логарифма будет больше 10%. С точностью до 4% при d2/d1 < 2 в практических расчетах рекомендуется пользоваться формулой для плоской стенки: ,
, ,
, ,
, .
.















 ,
, ,
, ,
, и
и  - термическое сопротивление внешней теплоотдачи соответственно от горячего теплоносителя к стенке и от стенки к холодному теплоносителю.
- термическое сопротивление внешней теплоотдачи соответственно от горячего теплоносителя к стенке и от стенки к холодному теплоносителю. ,
,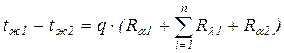
 ,
, - температурный напор, заданный условиями задачи;
- температурный напор, заданный условиями задачи; ,
,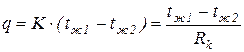 или
или 
 ,
, ,
,  , tc(n+1)=tc2.
, tc(n+1)=tc2. ,
, ,
, ,
, и
и 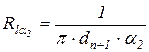 - термические сопротивления внутренней и внешней теплоотдачи на единицу длины.
- термические сопротивления внутренней и внешней теплоотдачи на единицу длины.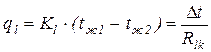 ,
,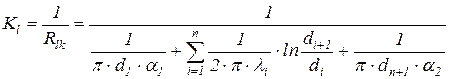 ,
, ,
,


