Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет параметров уравнений линейной и нелинейной парной регрессииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Расчет параметров линейной парной регрессии Парная линейная регрессия имеет вид: ŷx = a + b · x, где ŷx – результативный признак, характеризующий теоретические цены жилья на первичном рынке; x – фактор (себестоимость строительства); a, b – параметры, подлежащие определению. Построение уравнения регрессии сводится к оценке ее параметров. Для оценки параметров регрессии используется метод наименьших квадратов. Он позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака (цены жилья на первичном рынке) y от теоретических ŷx будет минимальной. В этом случае для определения параметров a и b линейной регрессии необходимо решить следующую систему уравнений:
На основании исходных данных выполнены расчеты, которые при Таблица 2.1
С учетом обозначений при n = 12
Значения параметров линейной регрессии вычисляются по формулам: b = ( a =
Тогда уравнение регрессии, являющееся линейной моделью цен жилья на первичном рынке в зависимости от себестоимости строительства, примет вид: ŷx = 2,643 · x – 38,795. На Рис. 5 представлены опытные значения стоимости квадратного метра
Рис. 5 жилья на первичном рынке и его себестоимости, а также теоретические значения стоимости квадратного метра жилья на первичном рынке в Приволжском федеральном округе. На Рис. 6 выполнено построение линейной функции регрессии.
Расчет параметров степенной парной регрессии Степенная парная регрессия относится к нелинейным регрессиям по оцениваемым параметрам. Однако она считается внутренне линейной, так как логарифмирование ее приводит к линейному виду. Таким образом, построению степенной модели
предшествует процедура линеаризации переменных. Линеаризация позволяет использовать для определения параметров функции регрессии метод наименьших квадратов. При этом оценки параметров будут вычислены по алгоритму, изложенному в 2.1.1. для этой цели проведем логарифмирование обеих частей уравнения: lg ŷ = lg a + b lg x. Обозначим через Ŷ = lg ŷ; X = lg x; A = lg a. Тогда уравнение примет вид: Ŷ = A + b X. Как отмечалось, для расчета параметров А и b используются соотношения метода наименьших квадратов, поскольку в новых переменных Y и X соотношение стало линейным, а следовательно, оценки параметров будут состоятельными, несмещенными и эффективными. Весь предварительный расчет параметров степенной функции регрессии аналогично линейной сведен в табл. 2.2. Таблица 2.2
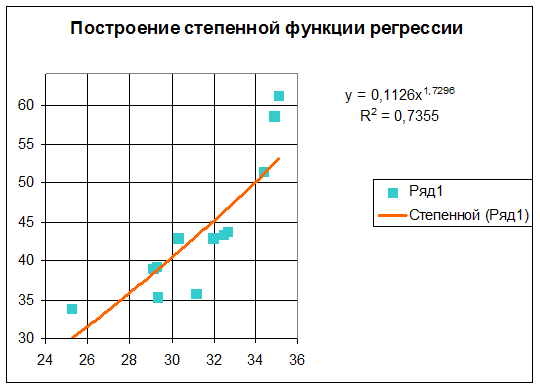
Тогда b = ( A = Таким образом, степенное уравнение регрессии с учетом логарифмических переменных будет иметь вид: Ŷ = –2,184 + 1,729· X. Выполнив его потенцирование, получим: ŷ x = 0,113 x 1,729 Подставляя в последнее уравнение фактические значения x, получаем теоретическое значение ŷx. Эти значения приведены в табл. 2.2. На Рис. 7 представлены опытные значения стоимости квадратного метра жилья на первичном рынке и его себестоимости, а также теоретические значения стоимости квадратного метра жилья на первичном рынке в Приволжском федеральном округе. На Рис. 8 выполнено построение степенной функции регрессии.
Рис. 7
Рис.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 723; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.71.166 (0.007 с.) |


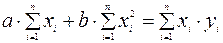
 = 12 представлены в табл. 2.1
= 12 представлены в табл. 2.1






 %
%
 = (y 1 + y 2 + … + y 12)/12;
= (y 1 + y 2 + … + y 12)/12;  = (x 1 + x 2 + … + x 12)/12;
= (x 1 + x 2 + … + x 12)/12; = (y 1 x 1 + y 2 x 2 + … + y 12 x 12)/12;
= (y 1 x 1 + y 2 x 2 + … + y 12 x 12)/12;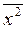 = (x 12 + x 22 + … + x 12)/12; Sx 2 =
= (x 12 + x 22 + … + x 12)/12; Sx 2 = 
 2.
2. )/(
)/( = 43,978 – 2,643 × 31,318 = – 38,795.
= 43,978 – 2,643 × 31,318 = – 38,795.
 Рис. 6
Рис. 6







 –
– 
 )/ Sx 2 = (12,972 – 3,44·3,767)/(11,843 – 3,44·3,44) = 1,729;
)/ Sx 2 = (12,972 – 3,44·3,767)/(11,843 – 3,44·3,44) = 1,729;