
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Фрагмент расчета простого и сложного дискретного обновления паркаСодержание книги
Поиск на нашем сайте
2. Расчет показателей ВС парка при случайном списании. Этот расчет основан на использовании закономерностей процесса восстановления (закономерности III вида, изученные в разделе теоретических основ дисциплины "Техническая эксплуатация автомобилей"). При этом весь наличный парк рассматривается в качестве восстанавливаемой технической системы, состоящей из элементов - отдельных автомобилей. Поток замен списываемых автомобилей во время существования парка i описывается, как это было показано в теоретических основах ТЭА, ведущей функцией Ω(i) и параметром потока отказов (списаний) и замен (поставок) ω(i). Ведущая функция определяет накопленное число событий (в данном случае замен списанных автомобилей) к определенной наработке i большой системы - парка автомобилей. Разница Ω(i+i) - Ω(i) =m(xi) определяет число событий в интервале наработок системы (i+1) - i.
где, n - количество изделий в парке. Для этого случая
где Fk - интегральная функция распределения наработки при k-й замене инвентарного автомобиля парка; i - календарное время работы парка. Смысл этого выражения состоит в том, что за фактический календарный срок существования парка автомобилей данной конструкции (i=20...25 лет) будет несколько (k) списаний и замен каждого списочного автомобиля (вернее его гаражного №). В случае нормального закона распределения наработки до списания автомобиля функция Ω(i) может быть определена аналитически по следующей формуле:
σ - среднеквадратические отклонения наработки до списания; k - число замен каждого списочного автомобиля; Ф(z) - нормированная функция для выражения:
Функция Ф(z) табулирована (см. прилож. 2), т.е. рассчитав значение z, по стандартной таблице определяют величину Ф(z).
Рассмотрим пример № 2 последовательности расчета случайного списания при следующих исходных данных:
Интервал календарного времени существования парка принят в 1 год, т.е. размер списания и компенсирующей поставки определяется в расчете на 1 год. Расчет проводится для i=16, т.е. 16 календарных лет существования парка. Заданный размер парка, который необходимо поддерживать Ai = const = 100 автомобилей. Последовательность расчета: 1) Определяем число замен в первом календарном интервале работы парка i=1. Так как фактические наработки при первом списании находятся в интервале х±3σ, т.е. от 2 до 8 лет, число списаний и замен автомобилей при i == Ω(i)=0, и расчет начинаем с i=2 года. 2) При календарном сроке службы парка i+1=2: а) для первых замен имеем i=2; k=1;
Вероятность первых замен F1(2)=Ф(-3) = 0,0013 (приложение 2); б) для вторых замен i=2; k=2; x=5; σ=1.
в) так как вероятность вторых замен при i=2 равна 0, то не будет третьих и последующих замен. Поэтому накопленное относительное количество замен при i=2 согласно формуле (11) равно: Ω(2) = 0,0013 + 0 = 0,0013 на один списочный автомобиль. 3) Подобные расчеты проводятся для i = 3,4,5...i=16. Например, для календарной продолжительности работы парка i=8 имеем: а) первые замены i=8; k=1;
т.е. фактически весь списочный состав парка к этому моменту (i=8) будет обновлен, как минимум, один раз. б) вторые замены (k=2)
в) третьи замены (k=3)
4) Общее накопленное количество замен на один инвентарный автомобиль за i=8 равно Ω(8)=F1(8)+F2(8)+ F3(8)=0,9987+0,082+0=1,081, т.е. это общее накопленное количество замен в парке на один инвентарный (списочный) автомобиль. Иными словами, за 8 лет существования парка каждый списочный автомобиль обновился (списание-замена) в среднем около 1,1 раза. 5) Полученные таким образом накопленные значения Ω(i) сводим в табл. 2.2 6) Определяем по формуле (9) параметр потока списаний по интервалам календарного периода существования парка (i+1)-i:
т.к. интервал расчетов принят один год. Таблица 2.2
|
|||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 278; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.255.63 (0.009 с.) |

 (9)
(9)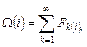 (10)
(10) (11)
(11) - средняя наработка до списания автомобиля;
- средняя наработка до списания автомобиля; (12)
(12)
 =5; σ=1 и имеем
=5; σ=1 и имеем








