
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Правила построения векторных диаграмм.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Векторная диаграмма - это положение вектора на комплексной плоскости Топографическая диаграмма напряжения – это положение комплексных потенциалов точек соединения схемы на комплексной плоскости. Правило № 1 Любую синусоидальную величину можно представить ввиде вращающегося вектора с угловой скоростью ɷ и длинной равной амплитуде. Правило №2 Начальное положение вектора определяется углом начальной фазы. Правило №3 В одних и тех же осях можно строить векторы токов, напряжений, ЭДС одной и той же частоты. Правило №4 Так как вращения векторов одинаковы по отношению друг к другу, они остаются неподвижными, поэтому векторы не вращаются, рассматривают в нулевой момент времени. Правило №5 Отказавшись от вращения можно строить векторы не только амплитудных, но и действующих значений. Правило №6 Векторы можно складывать по правилу параллелограмма. Правило №7 Если начальные фазы не заданы, то начальные фазы одного параметра можно принять равное нулю, остальные начальные фазы определяются из этого параметра. Изображение синусоидальных величин в комплексной форме. Геометрические операции с векторами можно заменить алгебраическими операциями с комплексными числами, что существенно повышает точность получаемых результатов.
показательной тригонометрической алгебраической Например, ЭДС Фазовый угол В соответствии с тригонометрической формой записи мнимая составляющая комплексного числа определяет мгновенное значение синусоидально изменяющейся ЭДС:
Комплексное число
Параметр Параметр
Вообще говоря, умножение вектора на оператор поворота Следовательно, мгновенное значение синусоидальной величины равно мнимой части без знака “ j” произведения комплекса амплитуды Переход от одной формы записи синусоидальной величины к другой осуществляется с помощью формулы Эйлера:
Если, например, комплексная амплитуда напряжения задана в виде комплексного числа в алгебраической форме: - то для записи ее в показательной форме, необходимо найти начальную фазу Тогда мгновенное значение напряжения: где При записи выражения для определенности было принято, что
а при
или
Если задано мгновенное значение тока в виде Следует указать, что при сложении и вычитании комплексов следует пользоваться алгебраической формой их записи, а при умножении и делении удобна показательная форма. Итак, применение комплексных чисел позволяет перейти от геометрических операций над векторами к алгебраическим над комплексами. Так при определении комплексной амплитуды результирующего тока Закон Ома в комплексной форме. U = U R + U L + U C = UR + jUL – jUC = IR + jIXL – jIXC = I (R+ j) (XL - XC) = I Z Законы Кирхгофа в комплексной форме. 1 закон Кирхгофа: I = I R+ I L+ I C=IR – jIL + jIC=U/R – jU/XL+ U/jXC 2 закон Кирхгофа: Σ E = Σ IZ + Σ U
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 540; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.51.81 (0.01 с.) |

 Каждому вектору на комплексной плоскости соответствует определенное комплексное число, которое может быть записано в:
Каждому вектору на комплексной плоскости соответствует определенное комплексное число, которое может быть записано в: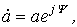
 или
или - формах.
- формах.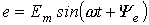 , изображенной на рис. 7 вращающимся вектором, соответствует комплексное число
, изображенной на рис. 7 вращающимся вектором, соответствует комплексное число .
. определяется по проекциям вектора на оси “+1” и “+j” системы координат, как
определяется по проекциям вектора на оси “+1” и “+j” системы координат, как .
. ,
,
 удобно представить в виде произведения двух комплексных чисел:
удобно представить в виде произведения двух комплексных чисел: ,
,
 , соответствующий положению вектора для t=0 (или на вращающейся со скоростью w комплексной плоскости), называют комплексной амплитудой:
, соответствующий положению вектора для t=0 (или на вращающейся со скоростью w комплексной плоскости), называют комплексной амплитудой:  , а параметр
, а параметр  - комплексом мгновенного значения.
- комплексом мгновенного значения. является оператором поворота вектора на угол wt относительно начального положения вектора.
является оператором поворота вектора на угол wt относительно начального положения вектора. есть его поворот относительно первоначального положения на угол ±a.
есть его поворот относительно первоначального положения на угол ±a. .
. ,
,
 ,
, , т.е. угол, который образует вектор
, т.е. угол, который образует вектор  с положительной полуосью +1:
с положительной полуосью +1: .
. ,
, .
. , т.е. что изображающий вектор находится в первом или четвертом квадрантах. Если
, т.е. что изображающий вектор находится в первом или четвертом квадрантах. Если  , то при
, то при  (второй квадрант)
(второй квадрант) ,
,
 (третий квадрант)
(третий квадрант)

 , то комплексную амплитуду записывают сначала в показательной форме, а затем (при необходимости) по формуле Эйлера переходят к алгебраической форме:
, то комплексную амплитуду записывают сначала в показательной форме, а затем (при необходимости) по формуле Эйлера переходят к алгебраической форме: .
.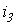 по рис. 5 получим:
по рис. 5 получим:
 ;
; .
.


