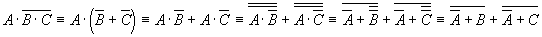Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Установление истинности сложных высказываний.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пример 1. Установить истинность высказывания
Из таблицы видно, что данное высказывание истинно только в случае, когда А=0, В=1, С=1. Во всех остальных случаях оно ложно. Эквивалентность высказываний. С помощью таблиц истинности можно установить эквивалентность двух или нескольких высказываний. Высказывания называются эквивалентными, если соответствующие значения каждого из них совпадают в таблице истинности. Пример 2. Утверждается, что высказывание А+В· С эквивалентно высказыванию (А+В)· (А+С)
Сравнивая 5-ю и 8-ю колонки убеждаемся, что все значения, получаемые по формуле А+В· С, совпадают со значениями, получаемыми по формуле (А+В)· (А+С), т.е. высказывания эквивалентны (равносильны). Одно может заменить другое. Тавтология. Пусть дано высказывание А·
Рассмотрим высказывание В+
Высказывания, истинность которых постоянна и не зависит от истинности входящих в них простых высказываний, а определяется только их структурой, называются тождественными или тавтологиями. Пример 3. Докажите тавтологию (XÙ Y)® (XÚ Y)
Т.к. высказывание (XÙ Y)® (XÚ Y) всегда истинно, то оно является тавтологией. Пример 4. Докажите тавтологию ((X® Y)Ù (Y® Z))® (X® Z)
Из таблицы видно, что исследуемое высказывание - тавтология, т.к. оно истинно постоянно. Вопросы и задания. 1. Какому из ниже приведенных высказываний: а) 2. Установите с помощью таблиц истинности, какие из следующих формул - тавтологии: г) ж) (X® Y)« 3. Установить истинность высказывания 4. Эквивалентны ли высказывания: 5. Установить, является ли данное высказывание тавтологией: 6. Для каждой формулы придумайте формализуемые ими предложения: 7. Из простых высказываний: “Виктор хороший пловец” - А; “Виктор хорошо ныряет” - В; “Виктор хорошо поет” - С, составлено сложное высказывание, формула которого имеет вид: 8. Установить истинность высказываний: 9. Установить истинность высказываний: Законы логики Равносильности формул логики высказываний часто называют законами логики. 1-й закон сформулирован древнегреческим философом Аристотелем. Закон тождества утверждает, что мысль, заключенная в некотором высказывании, остается неизменной на протяжении всего рассуждения, в котором это высказывание фигурирует. Закон противоречия говорит о том, что никакое предложение не может быть истинно одновременно со своим отрицанием. Закон исключенного третьего говорит о том, что для каждого высказывания имеются лишь две возможности: это высказывание либо истинно либо ложно. Третьего не дано. “Сегодня я получу 5 либо не получу”. Истинно либо суждение, либо его отрицание. Закон двойного отрицания. Отрицать отрицание какого-нибудь высказывания - то же, что утверждать это высказывание. Законы идемпотентности. В алгебре логики нет показателей степеней и коэффициентов. Конъюнкция одинаковых “сомножителей” равносильна одному из них. Законы коммутативности и ассоциативности. Конъюнкция и дизъюнкция аналогичны одноименным знакам умножения и сложения чисел. Смысл законов де Моргана (Август де Морган (1806-1871) - шотландский математик и логик) можно выразить в кратких словесных формулировках: Доказать законы логики можно: 2) C Ù (C Ú U) º C × C +C × U º C +C × U º C (1 + U) º C (Закон поглощения) Задание. Доказать законы логики с помощью таблиц истинности. Тождественные преобразования Упрощение формул. Пример 1. Упростить формулу (АÚВ)· (АÚС) 2. Преобразования “поглощение” и “склеивание” Пример 2. Упростить выражение АÚ A · B Решение. A ÚA · B º A (1 Ú B) º A - поглощение Пример 3. Упростить выражение A · B Ú A · 3. Всякую формулу 4. Любую формулу можно тождественно преобразовать так, что в ней не будут использованы: Пример 5. Преобразовать формулу Пример 6. Преобразовать формулу
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 2817; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.006 с.) |

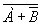 · С
· С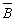
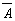 и необходимо составить таблицу истинности.
и необходимо составить таблицу истинности. ложно, истинность его не зависит от истинности высказывания А.
ложно, истинность его не зависит от истинности высказывания А. (A+C); б)
(A+C); б)  +B; в)
+B; в)  +C); г) A+
+C); г) A+  ;
; (B+C)
(B+C) «
« ); б)
); б) 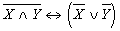 ; в)
; в)  ;
; ; д) (X® Y)«(Y® X); е) (X® Y)«
; д) (X® Y)«(Y® X); е) (X® Y)« ;
; .
.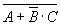
 и
и  ?
?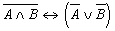 ; б)
; б) 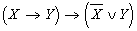
 ; б)
; б)  .
.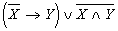 ; б)
; б)  ;
;  ,
,  ,
,  ;
; ,
,  ,
,  ;
;  ,
,  ,
,  ;
; ,
, 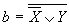 ,
,  .
. Закон противоречия
Закон противоречия Закон исключенного третьего
Закон исключенного третьего Закон двойного отрицания
Закон двойного отрицания ,
,  Законы де Моргана
Законы де Моргана  Ú U) º U, (C Ù U) Ú (
Ú U) º U, (C Ù U) Ú ( º A (B Ú
º A (B Ú  можно преобразовать так, что в ней не будет отрицаний сложных высказываний - все отрицания будут применяться только к простым высказываниям.
можно преобразовать так, что в ней не будет отрицаний сложных высказываний - все отрицания будут применяться только к простым высказываниям. так, чтобы не было отрицаний сложных высказываний.
так, чтобы не было отрицаний сложных высказываний.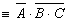
 применим еще раз формулу де Моргана, получим:
применим еще раз формулу де Моргана, получим: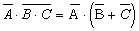
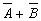 так, чтобы в ней не использовались знаки логического сложения.
так, чтобы в ней не использовались знаки логического сложения.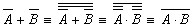
 так, чтобы в ней не использовались знаки логического умножения.
так, чтобы в ней не использовались знаки логического умножения.