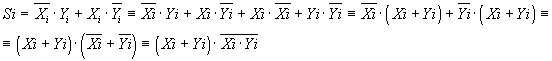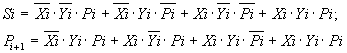Введение в математическую логику и теорию автоматов.
Введение в математическую логику и теорию автоматов.
1. Понятие о науке логике.
2. Алгебра высказываний. Высказывания. Простые и сложные высказывания.
3. Основные операции алгебры высказываний.
4. Таблицы истинности. Эквивалентные высказывания.
5. Законы логики.
6. Тождественные преобразования.
7. Логические основы построения ЭВМ.
8. Структурные формулы и функциональные схемы логических устройств.
9. Триггер.
10. Сумматор.
11. Регистры.
12. Шифраторы. Дешифраторы.
13. Счетчики.
Понятие о науке логике
Logos (греч.) - слово, понятие, рассуждение, разум. Слово “логика” обозначает совокупность правил, которым подчиняется процесс мышления или обозначает науку о правилах рассуждения и тех формах, в которых оно осуществляется. Логика изучает абстрактное мышление как средство познания объективного мира, исследует формы и законы, в которых происходит отражение мира в процессе мышления.
Основными формами абстрактного мышления являются: ПОНЯТИЯ, СУЖДЕНИЯ, УМОЗАКЛЮЧЕНИЯ.
ПОНЯТИЕ - форма мышления, в которой отражаются существенные признаки отдельного предмета или класса однородных предметов: портфель трапеция ураганный ветер.
СУЖДЕНИЕ - мысль, в которой что-либо утверждается или отрицается о предметах. Суждения являются повествовательными предложениями, истинными или ложными. Они могут быть простыми и сложными: Весна наступила, и грачи прилетели.
УМОЗАКЛЮЧЕНИЕ - прием мышления, посредством которого из исходного знания получается новое знание; из одного или нескольких истинных суждений, называемых посылками, мы по определенным правилам вывода получаем заключение. Есть несколько видов умозаключений.
Все металлы - простые вещества.
Литий - металл.
Литий - простое вещество.
Чтобы достичь истины при помощи умозаключений, надо соблюдать законы логики.
ФОРМАЛЬНАЯ ЛОГИКА - наука о законах и формах правильного мышления.
МАТЕМАТИЧЕСКАЯ ЛОГИКА изучает логические связи и отношения, лежащие в основе дедуктивного (логического) вывода.
Формальная логика связана с анализом наших обычных содержательных умозаключений, выражаемых разговорным языком. Математическая логика изучает только умозаключения со строго определенными объектами и суждениями, для которых можно однозначно решить, истинны они или ложны.
Умение правильно рассуждать необходимо в любой области человеческой деятельности: науке и технике, юстиции и дипломатии, планировании, военном деле и т.д.
Но хотя умение это восходит к древнейшим временам, логика, т.е. наука о том, какие формы рассуждений правильны, возникла лишь немногим более 2 тысяч лет назад.
Этапы развития логики.
1-й этап связан с работами ученого и философа Аристотеля (384-322 гг. до н.э.). Он пытался найти ответ на вопрос “как мы рассуждаем”, изучал “правила мышления”. Аристотель впервые дал систематическое изложение логики. Он подверг анализу человеческое мышление, его формы - понятие, суждение, умозаключение и рассмотрел мышление со стороны строения, структуры, то есть с формальной стороны. Так возникла формальная логика.
Аристотель исследовал различные формы рассуждений и их комбинаций, ввел понятие силлогизма, т.е. рассуждения, в котором из заданных двух суждений выводится третье.
Например:
1. “Все млекопитающие имеют скелет. Все киты - млекопитающие. Следовательно, все киты имеют скелет.”
2. “Все квадраты - ромбы, все ромбы - параллелограммы. Следовательно, все квадраты - параллелограммы.”
В общем виде этот силлогизм имеет форму:
“Все а суть в, все в суть с. Следовательно, все а суть с.”
А вот пример силлогизма неправильной формы:
“Все квадраты - ромбы. Некоторые ромбы имеют острый угол. Следовательно, некоторые квадраты имеют острый угол.”
Значит, силлогизм, имеющий форму “Все а суть в, некоторые в суть с. Значит, некоторые а суть с” может привести и к ложным выводам.
Аристотель выделил все правильные формы силлогизмов, которые можно составить из рассуждений вида:
- “Все а суть в”
- “Некоторые а суть в”
- “Все а не суть в”
- “Некоторые а не суть в”
Логика, основанная на теории силлогизмов называется классической.
Доказано, что общее число силлогизмов, которые можно составить из рассуждений указанного вида, равно 256. Из них правильными являются лишь 24.
Для проверки правильности силлогизмов можно использовать метод геометрической иллюстрации логических рассуждений, который был предложен великим математиком XVIII в., петербургским академиком Л.Эйлером (1707 - 1783) и широко применялся английским математиком Дж. Венном (1834 - 1923)
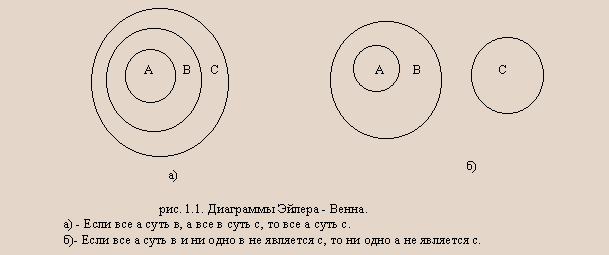
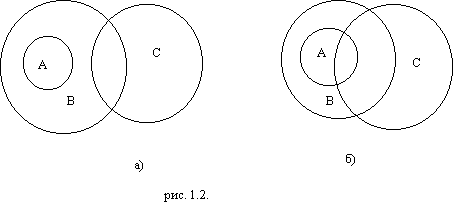
Рис. 1.2(а) поясняет почему не годится силлогизм “все а суть в, некоторые в суть с. Значит, некоторые а суть с”. Случайно может оказаться и так, что вывод будет истинным (рис. 1.2(б)). Но логика считает допустимым только такие формы рассуждений, которые гарантируют истинный результат во всех случаях, когда исходные утверждения истинны.
Использование диаграмм затруднительно в сложных случаях.
В конце XVI в. в алгебре словесная форма записи алгебраических выражений стала тормозить развитие науки и, чтобы облегчить выполнение алгебраических преобразований, была создана буквенная символика, позволяющая выполнять эти преобразования по строго определенным правилам.
Точно также, чтобы облегчить проверку и преобразование сложных цепочек рассуждений, было создано особое буквенное исчисление.
Оно получило название алгебры логики или математической логики.
2-й этап - появление математической или символической логики. Основы ее заложил немецкий ученый и философ Готфрид Вильгельм Лейбниц (1646-1716). Он попытался построить первые логические исчисления, считал, что можно заменить простые рассуждения действиями со знаками и привел правила. Но Лейбниц высказал только идею, а развил ее окончательно англичанин Джордж Буль (1815-1864). Буль считается основоположником математической логики как самостоятельной дисциплины. В его работах логика обрела свой алфавит, свою орфографию и грамматику. Недаром начальный раздел математической логики называют алгеброй логики, или булевой алгеброй.
Большой вклад в развитие математической логики внес русский математик П.С.Порецкий (1846-1907). П.С.Эренфест (1880-1933) доказал, что операции алгебры логики можно иллюстрировать на физических и технических явлениях, а, следовательно, и применять.
Развитие математической логики особенно активизировалось в середине нашего века в связи с ее использованием в ВТ и программировании.
Импликация.
Логическая операция, соответствующая союзу “если..., то...” называется импликацией.
Будем обозначать эту операцию символом ®. Запись А® В читается так: “если А, то В”, либо “А имплицирует В”.
С - “Если число n делится на 4, то оно делится на 2”
D - “Если Иванов увлечен математикой, то Петров ничем, кроме хоккея, не интересуется.”
Эквиваленция.
Логическая операция, соответствующая союзу “тогда и только тогда, когда” называется эквиваленцией.
Введем для обозначения эквиваленции символ «.
Запись А «читается так: “А тогда и только тогда, когда В”.
Когда мы говорим “А тогда и только тогда, когда В”, то имеем в виду, что оба предложения А и В одновременно истинны, либо одновременно ложны.
Например, “Я поеду в Ленинград тогда и только тогда, когда ты поедешь в Киев.”
Задания и упражнения.
1. Даны простые высказывания:
А: “Петя умеет плавать”
В: “Сергей умеет прыгать”
С: “Алеша умеет стрелять”
Даны формулы сложных высказываний, составленные из этих простых. Прочтите их, используя смысл каждого простого высказывания:
1. А+В· 
2. 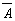 · В· · В· 
3. А· В· 
4. А · 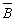 · С · С
5. А·  · · 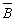
6. 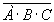
2. Даны простые высказывания:
“Данное число не кратное 3”
“Данное число больше 50”
Прочтите сложные высказывания:
1). А× 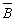 2). 2).  3). 3). 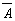 · · 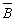
3. Прочтите формулы:
а). (A® D) Ù B; б). С U А Ù D; в). D Ù (B«( · C)) · C))
4. В состав истинного логического произведения входят три простых высказывания - A,B,C. Известно, что A и B - истинны. Может ли высказывание C быть одним из следующих:
а) “Дважды два равно семи”.
б) “Слоны живут в Африке и Индии”.
в) “5x + 3 = 11x”.
5. Дано высказывание: “Иванов является членом сборной команды “Алгоритм”. Какое из следующих высказываний есть логическим отрицанием данного?
а). Не Иванов является членом сборной команды “Алгоритм”.
б). Иванов является членом сборной команды не “Алгоритм”.
в). Иванов не является членом сборной команды “Алгоритм”.
г). Неверно, что Иванов является членом сборной команды “Алгоритм”.
6. Определите значения истинности высказываний:
а). “Если 16 делится на 4, то 16 делится на 2”.
б). “Если 17 делится на 4, то 17 делится на 2”.
в). “Если 18 делится на 4, то 18 делится на 2”.
г). “Если 18 делится на 2, то 18 делится на 4”.
д). “Если 2· 2=5, то 83 ¹ 500”.
е). “Если 2· 2=4, то 72 =81”.
ж). “Если телепатия существует, то некоторые физические законы требуют пересмотра”.
з). “16 делится на 4 тогда и только тогда, когда 16 делится на 2”.
и). “17 делится на 4 тогда и только тогда, когда 17 делится на 2”.
к). “18 делится на 4 тогда и только тогда, когда 18 делится на 2”.
л). “15 делится на 5 тогда и только тогда, когда 15 делится на 10”.
Таблицы истинности
Таблица истинности - это таблица, устанавливающая соответствие между всеми возможными наборами логических переменных, входящих в логическую функцию и значениями функции.
Таблицы истинности применяются для:
- вычисления истинности сложных высказываний;
- установления эквивалентности высказываний;
- определения тавтологий.
Тавтология.
Пусть дано высказывание А· 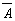 и необходимо составить таблицу истинности. и необходимо составить таблицу истинности.
Высказывание А·  ложно, истинность его не зависит от истинности высказывания А. ложно, истинность его не зависит от истинности высказывания А.
| А
| 
| А· 
| |
|
|
| |
|
|
| Рассмотрим высказывание В+ 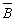 . .
В этом случае высказывание В+ 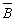 всегда истинно, независимо от истинности В. всегда истинно, независимо от истинности В.
| В
| 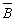
| В+ 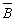
| |
|
|
| |
|
|
| Высказывания, истинность которых постоянна и не зависит от истинности входящих в них простых высказываний, а определяется только их структурой, называются тождественными или тавтологиями.
Различают тождественно-истинные и тождественно-ложные высказывания.
В формулах каждое тождественно-истинное высказывание заменяется 1, а тождественно-ложное - 0. Закон исключенного третьего.
A·  º 0 º 0
В+ 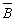 º 1 º 1
Пример 3. Докажите тавтологию (XÙ Y)® (XÚ Y)
Решение.
| X
| Y
| XÙ Y
| XÚ Y
| (XÙ Y)® (XÚ Y)
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| Т.к. высказывание (XÙ Y)® (XÚ Y) всегда истинно, то оно является тавтологией.
Пример 4. Докажите тавтологию ((X® Y)Ù (Y® Z))® (X® Z)
Решение.
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ F1 _ _ _ _ F2 _ _ _ _ _ F
| X
| Y
| Z
| X® Y
| Y® Z
| X® Z
| F1Ù F2
| (F1Ù F2) ® F3
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| Из таблицы видно, что исследуемое высказывание - тавтология, т.к. оно истинно постоянно.
Вопросы и задания.
1. Какому из ниже приведенных высказываний:
а)  (A+C); б) (A+C); б)  +B; в) +B; в)  +C); г) A+ +C); г) A+  ; ;
эквивалентно высказывание  (B+C) (B+C)
2. Установите с помощью таблиц истинности, какие из следующих формул - тавтологии:
а)  « « ); б) ); б) 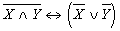 ; в) ; в)  ; ;
г)  ; д) (X® Y)«(Y® X); е) (X® Y)« ; д) (X® Y)«(Y® X); е) (X® Y)« ; ;
ж) (X® Y)« . .
3. Установить истинность высказывания 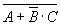
4. Эквивалентны ли высказывания:
 и и  ? ?
5. Установить, является ли данное высказывание тавтологией:
а) 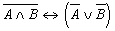 ; б) ; б) 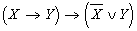
6. Для каждой формулы придумайте формализуемые ими предложения:
а)  ; б) ; б) 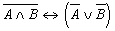 ; в) ; в)  . .
7. Из простых высказываний: “Виктор хороший пловец” - А; “Виктор хорошо ныряет” - В; “Виктор хорошо поет” - С, составлено сложное высказывание, формула которого имеет вид:
X=(A+C)· (A+B). Установить, эквивалентно ли высказывание Х высказыванию: “Виктор - хороший пловец и Виктор хорошо поет”.
8. Установить истинность высказываний:
а) 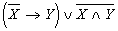 ; б) ; б)  ; ;
в) ((X1® X2)® X3)Ù (X3«X1); г) ((X® Y)Ù (Y® Z))® (X® Z).
9. Установить истинность высказываний:
а)  , ,  , ,  ; ;
б)  , ,  , ,  ; ;
в)  , ,  , ,  ; ;
г)  , , 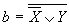 , ,  . .
Законы логики
Равносильности формул логики высказываний часто называют законами логики.
Знание законов логики позволяет проверять правильность рассуждений и доказательств.
Нарушения этих законов приводят к логическим ошибкам и вытекающим из них противоречиям.
Перечислим наиболее важные из них:
1. Xº X Закон тождества
2.  Закон противоречия Закон противоречия
3.  Закон исключенного третьего Закон исключенного третьего
4.  Закон двойного отрицания Закон двойного отрицания
5. XÙ Xº X, XÚ Xº C Законы идемпотентности
6. C Ù U º U Ù C, C Ú U º U Ú C Законы коммутативности (переместительности)
7. (C Ù U) Ù Z ºC Ù (U Ù Z), (C Ú U) Ú Z º C Ú (U Ú Z) - Законы ассоциативности (сочетательности)
8. C Ù (U Ú Z) º (C Ù U) Ú (C Ù Z), C Ú (U Ù Z) º (C Ú U) Ù (C Ú Z) - Законы дистрибутивности (распределительности)
9.  , ,  Законы де Моргана Законы де Моргана
10. XÙ 1º C, C Ú 0 º C
11. C Ù 0 º 0, C Ú 1 º 1
12. C Ù (C Ú U) º C, C Ú (C Ù U) º C Законы поглощения
13. (C Ú U) Ù ( Ú U) º U, (C Ù U) Ú ( Ú U) º U, (C Ù U) Ú ( Ú U) º U Законы склеивания Ú U) º U Законы склеивания
1-й закон сформулирован древнегреческим философом Аристотелем. Закон тождества утверждает, что мысль, заключенная в некотором высказывании, остается неизменной на протяжении всего рассуждения, в котором это высказывание фигурирует.
Закон противоречия говорит о том, что никакое предложение не может быть истинно одновременно со своим отрицанием.
“Это яблоко спелое” и “Это яблоко не спелое”.
Закон исключенного третьего говорит о том, что для каждого высказывания имеются лишь две возможности: это высказывание либо истинно либо ложно. Третьего не дано. “Сегодня я получу 5 либо не получу”. Истинно либо суждение, либо его отрицание.
Закон двойного отрицания. Отрицать отрицание какого-нибудь высказывания - то же, что утверждать это высказывание.
“ Неверно, что 2× 2¹ 4”
Законы идемпотентности. В алгебре логики нет показателей степеней и коэффициентов. Конъюнкция одинаковых “сомножителей” равносильна одному из них.
Законы коммутативности и ассоциативности. Конъюнкция и дизъюнкция аналогичны одноименным знакам умножения и сложения чисел.
В отличие от сложения и умножения чисел логическое сложение и умножение равноправны по отношению к дистрибутивности: не только конъюнкция дистрибутивна относительно дизъюнкции, но и дизъюнкция дистрибутивна относительно конъюнкции.
Смысл законов де Моргана (Август де Морган (1806-1871) - шотландский математик и логик) можно выразить в кратких словесных формулировках:
 - отрицание логического произведения эквивалентно логической сумме отрицаний множителей. - отрицание логического произведения эквивалентно логической сумме отрицаний множителей.
 - отрицание логической суммы эквивалентно логическому произведению отрицаний слагаемых. - отрицание логической суммы эквивалентно логическому произведению отрицаний слагаемых.
Доказать законы логики можно:
1) с помощью таблиц истинности;
2) с помощью равносильностей.
Докажем законы склеивания и поглощения с помощью равносильностей:
1) (C Ú U) Ù ( Ú U) º (C + U) × ( Ú U) º (C + U) × ( + U) º C × + U) º C ×  + U × + U ×  + U × U + C × U ºU × + U × U + C × U ºU ×  + U + C × U º U × + U + C × U º U ×  +U (1 + C) º U × +U (1 + C) º U ×  + U º U ( + U º U ( + 1) º U (Закон склеивания) + 1) º U (Закон склеивания)
2) C Ù (C Ú U) º C × C +C × U º C +C × U º C (1 + U) º C (Закон поглощения)
Задание. Доказать законы логики с помощью таблиц истинности.
Тождественные преобразования
Упрощение формул.
Пример 1. Упростить формулу (АÚВ)· (АÚС)
Решение.
а) Раскроем скобки (A Ú B) · (A ÚC) º A · A Ú A · C Ú B · A Ú B · C
б) По закону равносильности A · A º A, следовательно,
A · A Ú A · C ÚB · A Ú B · C º A ÚA · C Ú B · A Ú B · C
в) В высказываниях А и А· C вынесем за скобки А и используя свойство АÚ1º 1, получим АÚА· СÚ B · A Ú B · C º A ·(1 ÚС) Ú B · A Ú B · Сº A ÚB · A Ú B· С
г) Аналогично пункту в) вынесем за скобки высказывание А.
AÚB · A Ú B · Сº A (1ÚB)ÚB · Сº A Ú B · С
Таким образом, мы доказали закон дистрибутивности.
2. Преобразования “поглощение” и “склеивание”
Пример 2. Упростить выражение АÚ A · B
Решение. A ÚA · B º A (1 Ú B) º A - поглощение
Пример 3. Упростить выражение A · B Ú A · 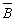
Решение.
A · BÚA ·  º A (B Ú º A (B Ú  ) º A - склеивание ) º A - склеивание
3. Всякую формулу  можно преобразовать так, что в ней не будет отрицаний сложных высказываний - все отрицания будут применяться только к простым высказываниям. можно преобразовать так, что в ней не будет отрицаний сложных высказываний - все отрицания будут применяться только к простым высказываниям.
Пример 4. Преобразовать формулу  так, чтобы не было отрицаний сложных высказываний. так, чтобы не было отрицаний сложных высказываний.
Решение.
1. Воспользуемся формулой де Моргана, получим:
 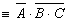
2. Для выражения  применим еще раз формулу де Моргана, получим: применим еще раз формулу де Моргана, получим:
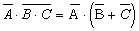
4. Любую формулу можно тождественно преобразовать так, что в ней не будут использованы:
- знаки логического сложения;
- знаки логического умножения.
А будут использованы:
- знаки отрицания и логического умножения;
- знаки отрицания и логического сложения.
Пример 5. Преобразовать формулу 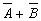 так, чтобы в ней не использовались знаки логического сложения. так, чтобы в ней не использовались знаки логического сложения.
Решение. Воспользуемся законом двойного отрицания, а затем формулой де Моргана.
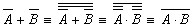
Пример 6. Преобразовать формулу  так, чтобы в ней не использовались знаки логического умножения. так, чтобы в ней не использовались знаки логического умножения.
Решение. Используя формулы де Моргана и закон двойного отрицания получим:
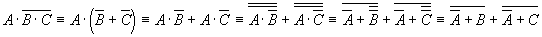
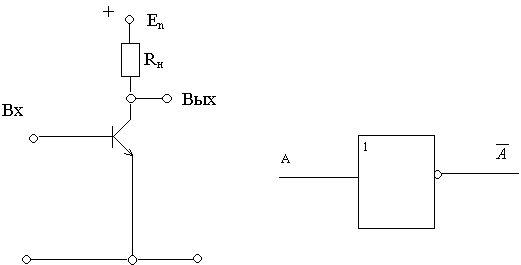
Элемент НЕ
| A
| 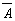
| |
|
| |
|
| При подаче на вход схемы сигнала низкого уровня (0) транзистор будет заперт, т.е. ток через него проходить не будет, и на выходе будет сигнал высокого уровня (1). Если же на вход схемы подать сигнал высокого уровня (1), то транзистор “откроется”, начнет пропускать электрический ток. На выходе за счет падения напряжения установится напряжение низкого уровня. Таким образом, схема преобразует сигналы одного уровня в другой, выполняя логическую функцию.
Элемент ИЛИ
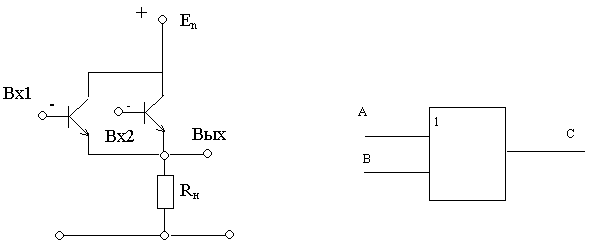
Функция “ИЛИ” - логическое сложение (дизъюнкция), ее результат равен 1, если хотя бы 1 из аргументов равен 1.
Здесь транзисторы включены параллельно друг другу. Если оба закрыты, то их общее сопротивление велико и на выходе будет сигнал низкого уровня (логический “0”). Достаточно подать сигнал высокого уровня (“1”) на один из транзисторов, как схема начнет пропускать ток, и на сопротивлении нагрузки установится также сигнал высокого уровня (логическая “1”).
Элемент И
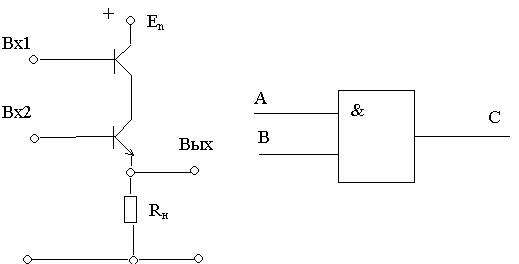
Если на входы Вх1 и Вх2 поданы сигналы низкого уровня (логические “0”), то оба транзистора закрыты, ток через них не проходит, выходное напряжение на Rн близко к нулю.
Пусть на один из входов подано высокое напряжение (“1”). Тогда соответствующий транзистор откроется, однако другой останется закрытым, и ток через транзисторы и сопротивление проходить не будет. Следовательно, при подаче напряжения высокого уровня лишь на один из транзисторов, схема не переключается и на выходе остается напряжение низкого уровня.
И лишь при одновременной подаче на входы сигналов высокого уровня (“1”) на выходе мы также получим сигнал высокого уровня.
Структурные формулы и функциональные схемы логических устройств
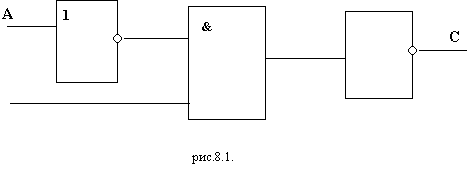
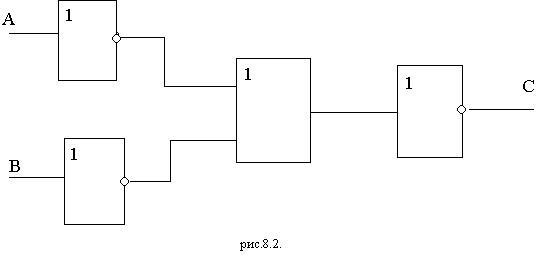
Соответствующие схемы называются функциональными. Анализируя функциональную схему, можно понять, как работает логическое устройство, т.е. дать ответ на вопрос: какую функцию она выполняет.
Не менее важной формой описания логических устройств является структурная формула. Покажем на примере как выписывают формулу по заданной функциональной схеме.
Ясно, что элемент “И” осуществляет логическое умножение значений 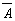 и В. и В.
Над результатом в элементе “НЕ” осуществляется операция отрицания, т.е. вычисляется значение выражения: 
Формула  и есть структурная формула логического устройства. и есть структурная формула логического устройства.
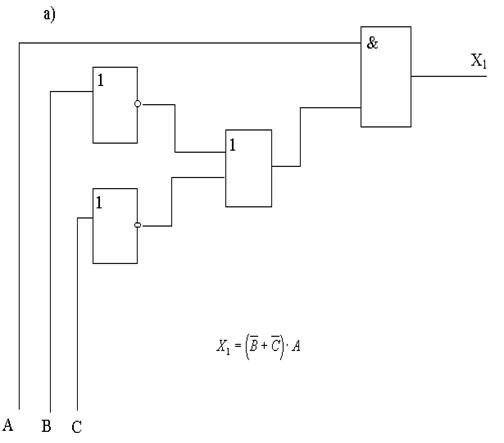
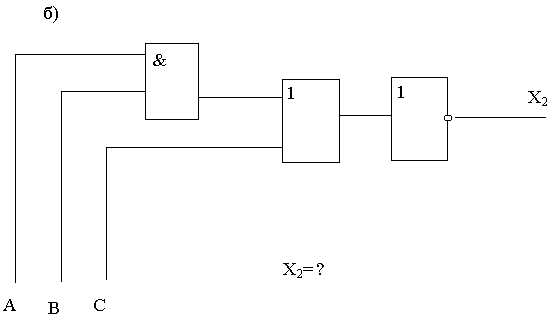
Задание 1. Для каждой из функциональных схем выписать соответствующую структурную формулу.

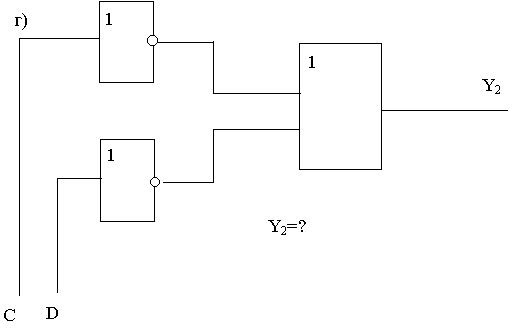

Триггер
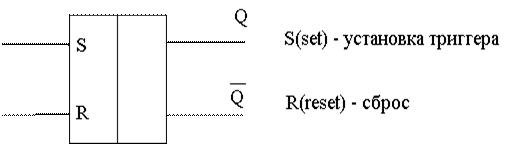
Триггер - это элементарный цифровой автомат, имеющий два устойчивых состояния равновесия (0 и 1), предназначенный для записи и хранения информации.
Под действием входных сигналов триггер может переключаться из одного устойчивого состояния в другое. Как, правило, триггер имеет 2 выхода: прямой и инверсный.
Q и  . .
Число входов зависит от выполняемых функций. По способу записи информации триггеры делятся на асинхронные и синхронные.
В асинхронных триггерах информация может изменяться в любой момент времени при изменении входных сигналов.
В синхронизирующих триггерах информация может меняться только в определенные моменты времени, задаваемые дополнительным синхронизирующим сигналом.
По функциональному построению различают схемы:
RS-, T-, D-, JK-триггеры
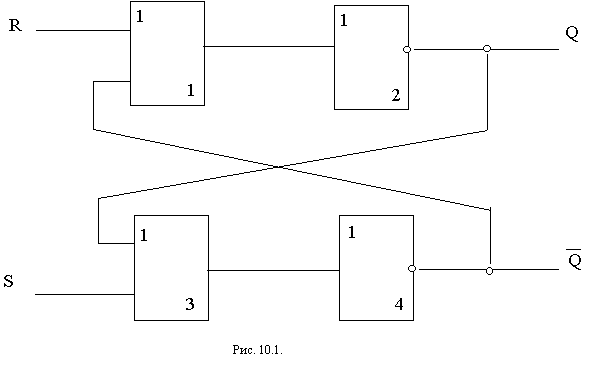
Асинхронный RS-триггер построен на 2-х логических элементах: ИЛИ - НЕ либо И – НЕ
Как он работает?
Пусть на вход элемента № 1 подан сигнал “1”, а на вход элемента № 3 - “0”. На выходе элемента № 1 независимо от того, какой второй сигнал поступит на вход, будет “1”, т.к. это элемент “ИЛИ” (по свойствам дизъюнкции). Пройдя через элемент № 2 сигнал примет значение “0” (Q=0). Следовательно, и на втором входе элемента № 3 установится сигнал “0”. На выходе элемента № 3 - “0”. Пройдя через элемент № 4 сигнал изменится на “1”. Следовательно,  = 1. = 1.
Убедимся, что данное устройство сохраняет информацию. Запомните, что S=0, R=1, Q=0,  =1. =1.
В момент прекращения входных сигналов (S=0, R=0) на выходе  =1. Это напряжение подается на вход элемента № 1. На выходе элемента № 1 сохраняется “1”, и на Q - сигнал “0”. На входах элемента №3 - “0”, следовательно =1. Это напряжение подается на вход элемента № 1. На выходе элемента № 1 сохраняется “1”, и на Q - сигнал “0”. На входах элемента №3 - “0”, следовательно  =1. =1.
Таким образом, при отсутствии на внешних входах сигналов “1” триггер поддерживает постоянное напряжение на своих выходах. Чтобы изменить напряжение на выходах триггера, надо подать сигнал “1” на вход элемента № 3. Тогда Q=1,  =0. =0.
| Вход
| Выход
| Режим
| | S
| R
| Q
| 
| Работы
| |
|
|
|
| Хранение
| |
|
|
|
| Запись 1
| |
|
|
|
| Запись 0
| |
|
| Х
| Х
| Запрещение ( ) )
| Cхема RS - триггера на элементах И - НЕ
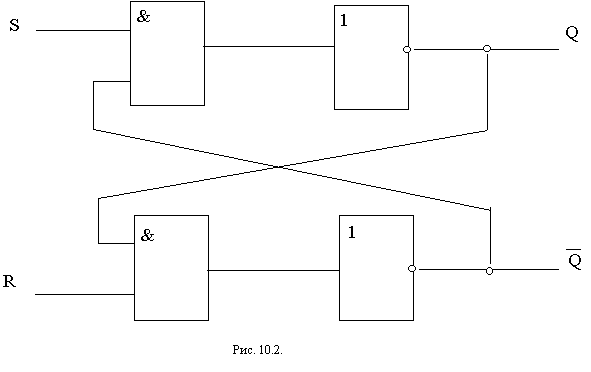
| Вход
| Выход
| Режим
| | S
| R
| Q
| 
| работы
| |
|
|
|
| Хранение
| |
|
|
|
| Запись 1
| |
|
|
|
| Запись 0
| |
|
| Х
| Х
| Запрещение ( ) )
|
Сумматор
Узел ЭВМ выполняющий арифметическое суммирование кодов чисел, называется сумматором. Операция суммирования осуществляется в сумматорах поразрядно с использованием одноразрядных суммирующих схем. При этом в каждом разряде требуется выполнить сложение трех двоичных цифр данного разряда первого слагаемого Хi цифры этого же разряда второго слагаемого Yi и цифры переноса Pi из соседнего младшего разряда.
И тогда такое суммирование разбивают на две аналогичные операции: суммирование двух цифр слагаемых и суммирование полученного результата с переносом из соседнего младшего разряда. Каждая из этих операций выполняется схемой, называемой полусумматором.
В таблице приведена логика работы сумматора на два входа X i и Yi. На его выходах образуется сумма Si данного разряда и осуществляется перенос Рi+1 в следующий старший разряд. По таблице можно составить логическое выражение для суммы Si и переноса Р i+1:


Преобразуем выражение для суммы к виду:
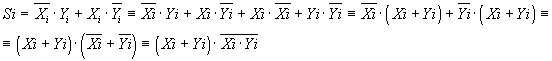
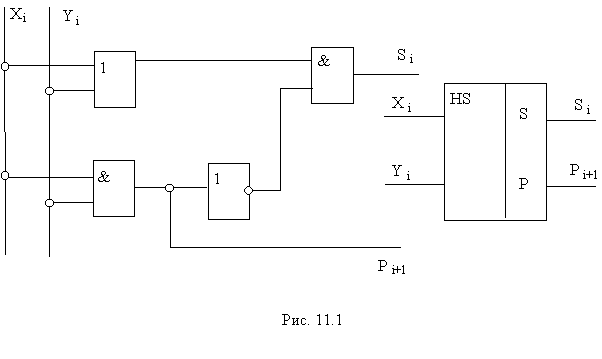
На рисунке 11.1 приведены функциональная схема полусумматора, составленная в соответствии с полученными логическими выражениями, и условное обозначение его. Схема является комбинационной и реализуется на логических элементах.
Логика работы одноразрядного сумматора на три входа или полного сумматора приведена в таблице А, где Xi, Yi - суммируемые двоичные цифры в i-м разряде, Pi - перенос из младшего разряда, Si - образующаяся сумма данного разряда и осуществляет перенос Pi+1 в следующий старший разряд.
Таблица А.
По таблице можно составить логические выражения:
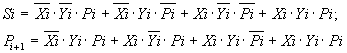
По этим выражениям также можно составить функциональную схему комбинационного сумматора с использованием соответствующих логических элементов. Однако, вначале целесообразно эти выражения преобразовать так, чтобы в формулах для Si и Pi+1 были по возможности одинаковые члены, что, естественно, сократит количество используемых элементов. Один из вариантов таких преобразований дают выражения:

которым соответствуют функциональная схема и условное обозначение сумматора, приведенные на рис.11.2.
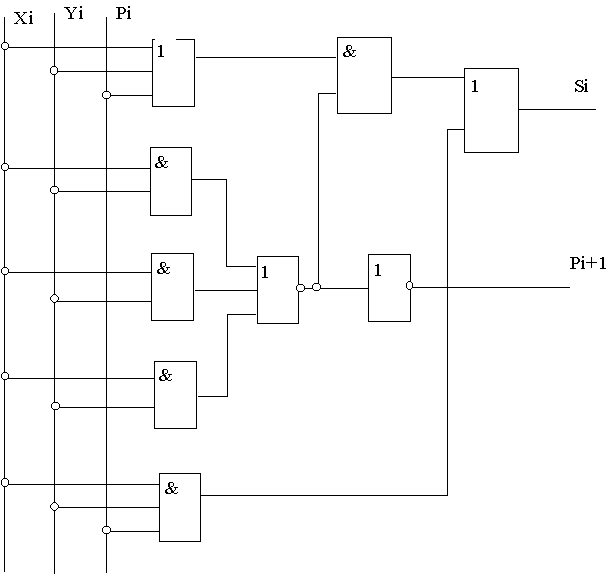
Комбинационный сумматор можно реализовать также с использованием двух полусумматоров и логического элемента ИЛИ, как показано на рис.11.3.
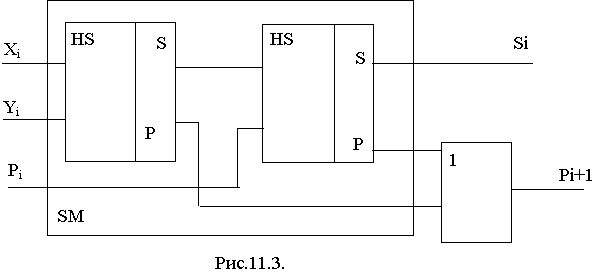
В реальных электронных схемах сумматор изображается так.
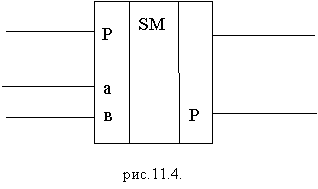

рис.11.5.
Эта схема называется одноразрядным сумматором.
| Число 1
| Число 2
| Ст.разряд
| Мл.разряд
| | Вх.1
| Вх.2
| Вых.1
| Вых.2
| |
|
|
|
| |
|
|
|
| |
|
|
|
| |
|
|
|
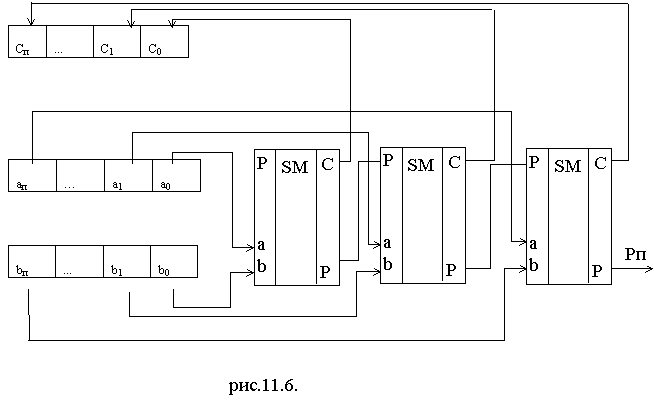
| На рис.11.6. показано, как из N сумматоров можно составить устройство для сложения двух N-разрядных двоичных кодов, это схема многоразрядного сумматора.
Регистры
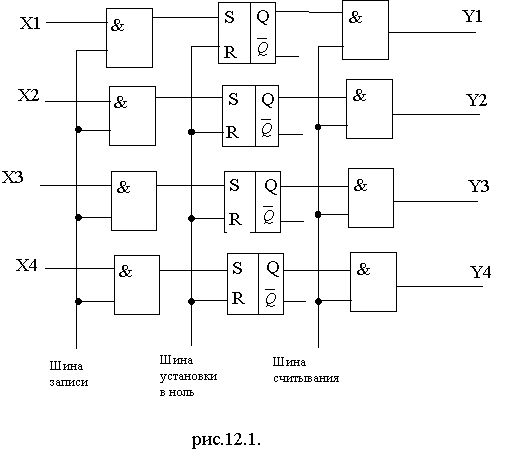
На рис.12.1. показана упрощенная схема регистра для записи чисел, имеющих 4 двоичных разряда.
Функциональный узел ЭВМ, состоящий из триггеров, предназначенный для запоминания многоразрядных кодов и выполнения над ними некоторых логических преобразователей называется регистром.
С помощью регистров можно выполнять следующие операции: установку, сдвиг, преобразование. Основными типами регистров являются параллельные и последовательные (сдвигающие).
Как происходит запись числа в регистр?
Каждая из входных схем “И” имеет 2 входа. Один из них - общий для всех (шина записи).
Если на шину записи подан “0”, то на всех схемах “И” также будет “0”. Однако, если на шину записи подается сигнал “1” - разрешение записи, то напряжение на выходах схем “И”, а, следовательно, и на S - входах триггеров, будет зависеть от того, какой сигнал поступает в этот момент на вторые входы схем “И”.
Если подать на шину записи последовательность 1001 (число 9), то первый и четвертый триггеры установятся в 1, а второй и третий - в 0.
Как только на шину считывания будет подан “1”, то на выходах схем “И” появится сигнал “1” в тех разрядах, в которых на основном выходе триггера была записана “1”.
В схемах реальных регистров используются и дополнительные выходы триггеров. На этих выходах создается так называемый обратный код.
Обратный код используется в ЭВМ для осуществления некоторых арифметических операций с двоичными числами.
Совокупность регистров, используемых ЭВМ для запоминания программы работы, исходных и промежуточных результатов называется оперативной памятью (ОП).
ОП содержит 215 регистров = 32768
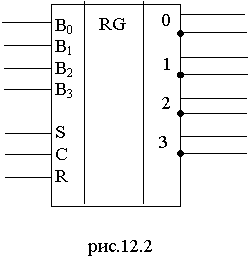
В ЭВМ применяются регистры 8, 16, 32, 48 и 64 разрядов.
Шифратор и дешифратор
Шифратор и дешифратор являются типовыми узлами ЭВМ.
Шифратор (кодер) преобразует единичный сигнал на одном из входов в n-разрядный двоичный код. Наибольшее применение он находит в устройствах ввода информации (пультах управления) д
|






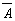 · В·
· В· 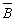 · С
· С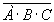
 3).
3).  · C))
· C)) (A+C); б)
(A+C); б)  +B; в)
+B; в)  +C); г) A+
+C); г) A+  ;
; (B+C)
(B+C) «
« ); б)
); б) 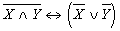 ; в)
; в)  ;
; ; д) (X® Y)«(Y® X); е) (X® Y)«
; д) (X® Y)«(Y® X); е) (X® Y)« ;
; .
.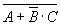
 и
и  ?
?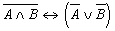 ; б)
; б) 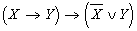
 ; б)
; б)  .
.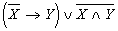 ; б)
; б)  ;
;  ,
,  ,
,  ;
; ,
,  ,
,  ;
;  ,
,  ,
,  ;
; ,
, 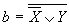 ,
,  .
. Закон противоречия
Закон противоречия Закон исключенного третьего
Закон исключенного третьего Закон двойного отрицания
Закон двойного отрицания ,
,  Законы де Моргана
Законы де Моргана  Ú U) º U, (C Ù U) Ú (
Ú U) º U, (C Ù U) Ú ( º A (B Ú
º A (B Ú  можно преобразовать так, что в ней не будет отрицаний сложных высказываний - все отрицания будут применяться только к простым высказываниям.
можно преобразовать так, что в ней не будет отрицаний сложных высказываний - все отрицания будут применяться только к простым высказываниям. так, чтобы не было отрицаний сложных высказываний.
так, чтобы не было отрицаний сложных высказываний.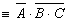
 применим еще раз формулу де Моргана, получим:
применим еще раз формулу де Моргана, получим: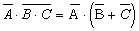
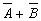 так, чтобы в ней не использовались знаки логического сложения.
так, чтобы в ней не использовались знаки логического сложения.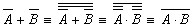
 так, чтобы в ней не использовались знаки логического умножения.
так, чтобы в ней не использовались знаки логического умножения.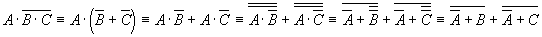






 и есть структурная формула логического устройства.
и есть структурная формула логического устройства.


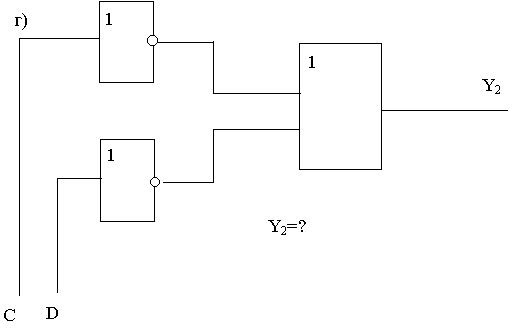

 .
.

 )
)