
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Абсолютный сдвиг и угол сдвигаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Абсолютный Сдвиг И Угол Сдвига Сопромат В результате сдвига одно поперечное сечение стержня смещается относительно другого на величину ( Малый угол ( Вопрос №19 ПОСТРОЕНИЕ ЭПЮР ПОПЕРЕЧНЫХ СИЛ И ИЗГИБАЮЩИХ МОМЕНТОВ Определение поперечных сил и изгибающих моментов - сечение 1 Отбросим правую часть балки и заменим ее действие на левую часть поперечной силой Поперечная сила в сечении 1 балки равна алгебраической сумме всех внешних сил, которые видим после закрытия Видим только реакцию опоры, направленную вниз. Таким образом, поперечная сила равна:
Знак «минус» нами взят потому, что сила Изгибающий момент в сечении 1 балки, равен алгебраической сумме моментов всех усилий, которые мы видим после закрытия отброшенной части балки, относительно рассматриваемого сечения 1.
Здесь знак «плюс» нами взят потому, что внешний момент M изгибает видимую нами часть балки выпуклостью вниз. (или потому, что противоположно направлен направлению изгибающего момента по правилу знаков) Определение поперечных сил и изгибающих моментов - сечение 2 В отличие от первого сечения, у силы реакции поперечная сила:
изгибающий момент:
Определение поперечных сил и изгибающих моментов - сечение 3 поперечная сила:
изгибающий момент:
Определение поперечных сил и изгибающих моментов - сечение 4 Теперь удобнее закрывать листком левую часть балки. поперечная сила:
изгибающий момент:
Определение поперечных сил и изгибающих моментов - сечение 5 поперечная сила:
изгибающий момент:
Определение поперечных сил и изгибающих моментов - сечение 1 поперечная сила и изгибающий момент:
По найденным значениям производим построение эпюры поперечных сил Емальянова:Раздел 2- вопрос 13,14 Внутренние силовые факторы при кручении Кручением называется нагружение, при котором в поперечном сечении бруса возникает только один внутренний силовой фактор - крутящий момент. Внешними нагрузками также являются две противоположно натравленные пары сил. Деформации и напряжения при кручении
где – длина стержня; – модуль сдвига; – полярный момент инерции площади поперечного сечения. Произведение называется жесткостью сечения при кручении.
В поперечном сечении стержня возникают касательные напряжения, направленные перпендикулярно радиусу (рис. 5.3) и вычисляемые по формуле
,
где ρ – расстояние от центра сечения до той точки, в которой вычисляют напряжение.
Рис. 5.3. Касательные напряжения при кручении: а – напряжения в точке; б – эпюра напряжений для круглого поперечного сечения; в – эпюра напряжений для кольцевого поперечного сечения
Максимальные касательные напряжения возникают в точках контура поперечного сечения, их определяют по формуле
,
где – полярный момент сопротивления сечения.
|
|||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1091; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.163.169 (0.007 с.) |

 ), называемую абсолютным сдвигом.
), называемую абсолютным сдвигом. ), на который изменится первоначально прямой угол (рис. 3.1, б) – это угол сдвига или относительный сдвиг. Угол сдвига выражается в радианах.
), на который изменится первоначально прямой угол (рис. 3.1, б) – это угол сдвига или относительный сдвиг. Угол сдвига выражается в радианах. и изгибающим моментом
и изгибающим моментом  . Для удобства вычисления закроем отбрасываемую правую часть балки листком бумаги, совмещая левый край листка с рассматриваемым сечением 1.
. Для удобства вычисления закроем отбрасываемую правую часть балки листком бумаги, совмещая левый край листка с рассматриваемым сечением 1. кН.
кН. вращает видимую нами часть балки относительно первого сечения против хода часовой стрелки (или потому, что одинаково направлена с направлением поперечной силы по правилу знаков)
вращает видимую нами часть балки относительно первого сечения против хода часовой стрелки (или потому, что одинаково направлена с направлением поперечной силы по правилу знаков)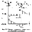 Видим два усилия: реакцию опоры
Видим два усилия: реакцию опоры  кН·м.
кН·м. кН;
кН; кН·м.
кН·м. кН;
кН; кН ·м.
кН ·м. кН;
кН; кН ·м.
кН ·м. кН;
кН; кН ·м.
кН ·м.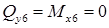 .
.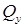 (рис. 7.7, б) и изгибающих моментов
(рис. 7.7, б) и изгибающих моментов  (рис. 7.7, в).
(рис. 7.7, в).


