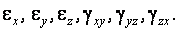Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Цуцарь- Раздел 2- вопрос 3,4Содержание книги
Поиск на нашем сайте
3. Внутренними силами являются силы, действующие между частицами, эти силы оказывают сопротивление изменению формы. Изменение формы тела под действием силы называют деформацией, а тело, претерпевшее деформацию, называют деформированным. Равновесие внутренних сил с момента приложения внешней силы нарушается, частицы тела перемещаются одна относительно другой до такого состояния и положения, когда возникающие между ними внутренние силы уравновешивают внешние силы и тело сохраняет приобретенную деформацию. Если внутренние силы малы и окажутся неспособными уравновесить внешние силы, то тело разрушается, разъединяясь на части. Для определения внутренних усилий используют метод сечений. Он заключается в выполнении четырех действий: · разрезать стержень плоскостью поперечного сечения на две части; · отбросить одну из частей стержня; · заменить действие отброшенной части стержня на оставшуюся часть внутренними усилиями; · уравновесить оставшуюся часть стержня. В общем случае можно составить шесть уравнений равновесия: суммы проекций всех сил на оси X, Y, Z и суммы моментов всех сил относительно этих осей. 4. Напряжения и деформации в точке Векторная величина, равная интенсивности внутреннего усилия в произвольной точке сечения стержня, называется напряжением. Различают нормальное напряжение
Напряжения можно вычислить на любой бесконечно малой площадке dA, проходящей через точку твердого тела. Совокупность напряжений на всех площадках, проходящих через точку, называется напряженным состоянием материала в точке. Напряжения измеряют в паскалях, Около некоторой точки К твердого тела выделим бесконечно малый элемент dx ´ dy ´ dz (рис. 1.5). Его деформированное положение в плоскости xKy показано пунктирными линиями. Определяют относительные линейные деформации в направлении координатных осей
При вращении координатных осей вокруг точки К указанные деформации будут изменяться. Совокупность относительных линейных деформаций и углов сдвига для произвольных осей, проведенных через выбранную точку, называется деформированным состоянием материала в точке. В общем случае оно определяется шестью относительными деформациями:
Дятлева: Раздел 2- вопрос 5,6 Крымко:Раздел 2-вопрос 7,8 Раздел 2 вопрос 7 Закон гука при растяжении и сжатии Первое по-настоящему научное исследование процесса упругого растяжения и сжатия вещества предпринял Роберт Гук. Первоначально в своем опыте он использовал даже не пружину, а струну, измеряя, насколько она удлиняется под воздействием различных сил, приложенных к одному ее концу, в то время как другой конец жестко закреплен. Ему удалось выяснить, что до определенного предела струна растягивается строго пропорционально величине приложенной силы, пока не достигает предела упругого растяжения (эластичности) и не начинает подвергаться необратимой нелинейной деформации (см. ниже). В виде уравнения закон Гука записывается в следующей форме: F = –kx где F — сила упругого сопротивления струны, x — линейное растяжение или сжатие, а k — так называемый коэффициент упругости. Чем выше k, тем жестче струна и тем тяжелее она поддается растяжению или сжатию. Знак минус в формуле указывает на то, что струна противодействуетдеформации: при растяжении стремится укоротиться, а при сжатии — распрямиться. Закон Гука лег в основу раздела механики, который называется теорией упругости. Выяснилось, что он имеет гораздо более широкие применения, поскольку атомы в твердом теле ведут себя так, будто соединены между собой струнами, то есть упруго закреплены в объемной кристаллической решетке. Таким образом, при незначительной упругой деформации эластичного материала действующие силы также описываются законом Гука, но в несколько более сложной форме. В теории упругости закон Гука принимает следующий вид: σ / η = E где σ — механическое напряжение (удельная сила, приложенная к поперечной площади сечения тела), η — относительное удлинение или сжатие струны, а Е — так называемый модуль Юнга, или модуль упругости, играющий ту же роль, что коэффициент упругости k. Он зависит от свойств материала и определяет, насколько растянется или сожмется тело при упругой деформации под воздействием единичного механического напряжения
раздел 2 вопрос 8
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 232; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.148.145.219 (0.005 с.) |

 , перпендикулярное плоскости сечения, и касательные напряжения
, перпендикулярное плоскости сечения, и касательные напряжения  ,
,  , лежащие в плоскости сечения.
, лежащие в плоскости сечения.
 и
и 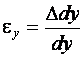 , а также угол сдвига
, а также угол сдвига  .
.