
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выбор электродвигателя для привода механизмаСодержание книги
Поиск на нашем сайте
В качестве исходных данных для выбора электродвигателя следует принять зависимость приведенного момента внешних сил от угла поворота входного звена Mпс=f(OK) и частоту вращения входного звена n1 в оборотах за минуту. Средний момент, который должен развивать электродвигатель в установившемся режиме, может быть определен из выражения
Тогда потребная мощность двигателя
где h - КПД передаточного механизма,
Основные параметры асинхронных электрических двигателей трехфазного тока с короткозамкнутым ротором можно определить из каталога двигателей [4] или базы данных. Они разделены на группы, в зависимости от синхронной частоты вращения ротора, определяемой числом пар полюсов статора: nс=3000, 1500, 1000 и 750 об/мин. У двигателей с большей частотой вращения ротора меньшие габариты и масса, но в этом случае увеличивается передаточное отношение привода, а также габариты и масса передаточного механизма. Для выбора оптимальной схемы электромеханического привода можно использовать специальную программу, имеющуюся на кафедре ОКММ. В первом приближении передаточное отношение привода Uпp можно принять равным 20…30, что соответствует использованию двухступенчатого цилиндрического редуктора (7…10 для одноступенчатого редуктора). Тогда ориентировочное значение частоты вращения ротора двигателя
Электродвигатель следует выбрать так, чтобы его синхронная частота вращения nс была меньше Oписание процедуры: Motor (Mpc: Massiv; n1, Umax, { входные параметры } Om1cp, Mpdcp, { выходные параметры } nc, nn, Pn, dk, lk, Massa, Delta: Real), где Mpc - массив значений приведенного момента внешних сил; n1 - средняя частота вращения кривошипа; Umax - максимально допустимое значение передаточного отношения привода; Om1cp - средняя угловая скорость кривошипа; Mpdcp - средний момент, который должен развивать двигатель; nс, nn - синхронная и номинальная частоты вращения ротора; Pn - номинальная мощность двигателя; dk, lk - диаметр и длина корпуса двигателя; Massa - масса двигателя; Delta - коэффициент неравномерности вращениякривошипа. При обращении к процедуре следует, кроме Mpc задать n1 и Umax. Процедура работает следующим образом. Сначала методом трапеций рассчитывается величина определенного интеграла в формуле (7), а, следовательно, и Mpdcp. Затем по формуле (9) рассчитывается Om1cp и по формуле (8) - Рд. Значение потребной мощности выводится на экран дисплея, после чего следует выбрать из каталога двигателей [4] или базы данных нужный электродвигатель. При использовании методических указаний [4] следует обратиться к той части таблицы, где помещены двигатели с синхронной частотой nc, ближайшей меньшей - синхронную и номинальную (асинхронную) частоту вращения; - номинальную мощность; - коэффициент перегрузки - диаметр корпуса двигателя; - длину корпуса двигателя; - массу двигателя. После этого на экране дисплея появится изображение механической характеристики двигателя - зависимости между моментом двигателя и частотой вращения ротора (рис. 13), с двумя вертикальными линиями, одна из которых соответствует номинальным параметрам двигателя, а вторая - средней рабочей нагрузке на двигатель, то есть рабочим параметрам при вращении ротора с постоянной угловой скоростью (d =0).
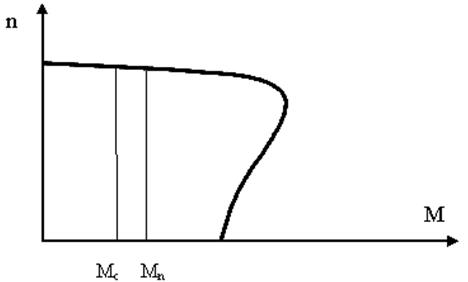
Рисунок 13 – Механическая характеристика асинхронного двигателя В действительности угловая скорость кривошипа, а, следовательно, и ротора двигателя, колеблется около среднего значения, и на экране дисплея можно наблюдать изменение диапазона колебания угловой скорости и вращающего момента двигателя при изменении коэффициента неравномерности вращения d с шагом, равным 0,01. Для увеличения d следует нажимать на клавишу “+”, а для уменьшения - на клавишу “‑”. При этом текущее значение d выводится на экран. Оценка оптимального значения d может быть выполнена следующим образом. Сначала необходимо принять во внимание практические рекомендации по выбору величины d для рассчитываемого типа механизма, а затем уточнить ее так, чтобы рабочий участок механической характеристики двигателя не попадал в зону неустойчивой работы двигателя или в зону генераторного режима, когда частота вращения ротора оказывается выше синхронной. Процедура позволяет провести корректировку выбора двигателя. После окончательного выбора с целью сокращения времени на отладку программы процедуру Motor целесообразно отключить, задав в программе величины, необходимые для последующих расчетов: n1, nc, nn, Pn, dk, lk, Massa, Delta. 10 ПОДБОР МАХОВИКА И ОПРЕДЕЛЕНИЕ ЗАКОНА ДВИЖЕНИЯ НАЧАЛЬНОГО ЗВЕНА Для решения задач настоящего этапа следует использовать процедуру Dinamo, которая входит в модуль Dinamika.tpu. Описание процедуры: Dinamo (n1, nc, nn, Pn, dk, lk, Massa, { входные параметры } Delta, Om10, r: Real; Mpc, Ip, Ip_1: Massiv; var Om1cp, Mpdcp, U, Ipm: Real; { выходные параметры } var Om1, Mpd, e1: Massiv). В качестве входных принимаются параметры, уже знакомые по процедуре Motor: n1, nc, nn, Pn, dk, lk, Massa, Delta, а также уже сформированные массивы Mpc, Ip, Ip_1. Входными являются также параметры Om10 и r, значение которых будет разъяснено ниже. Выходные параметры: Omlср, Mpdcp -то же, что и в процедуре Motor; U - передаточное отношение привода; Om1 - массив значений угловых скоростей кривошипа для 49 его положений; Mpd - массив значений приведенного к кривошипу момента двигателя; e1 - массив значений углового ускорения кривошипа. Процедура работает следующим образом. Вначале определяется передаточное отношение привода U, обеспечивающее требуемое значение средней частоты вращения кривошипа n1. Для этого используется линейная аппроксимация рабочего участка механической характеристики двигателя в форме
где, кроме уже известных величин k - коэффициент наклона характеристики двигателя,
Уравнение (11) является квадратным относительно искомого передаточного отношения, величину которого следует выписать с экрана дисплея. Момент инерции маховика, обеспечивающий требуемый коэффициент неравномерности вращения d, определяется по приближенной формуле
где Аизб - избыточная работа, равная разности работ сил сопротивления и движущих сил на участке их совместного действия, определяемая в процедуре приближенно. Поскольку значение Iм, определенное по формуле (13), также является приближенным, для его корректировки можно использовать коэффициент r, который вначале следует принять равным 1. В основу определения закона вращения кривошипа w1=f(j1 ) положено дифференциальное уравнение в форме
где Мпд и Мпс - приведенные к кривошипу момент, развиваемый двигателем, и момент внешних сил, определенный по формуле (4);
С учетом линейной аппроксимации рабочего участка механической характеристики двигателя уравнение (14) может быть представлено в виде
В рассматриваемой процедуре для решения этого дифференциального уравнения использован численный метод. Уравнение (16), записанное в конечных разностях в предположении, что на конечном интервале поворота кривошипа Dj1 все величины изменяются линейно, имеет вид
Зная значение угловой скорости
где Если условие (18) не выполняется, новому значению Процедура предусматривает возможность просмотра на экране полученного решения для такого числа оборотов, которое обеспечивает соблюдение условия (18). После выполнения этого условия процесс решения заканчивается и на экране появляется надпись «STOP». После этого процедура рассчитывает и выводит на экран значение
для определенного по формуле (13) значения момента инерции маховика, а также схематическое изображение в одинаковом масштабе выбранного двигателя и маховика и значения их массы. Причем габариты и масса маховика определяются для двух вариантов его установки: на валу двигателя и на валу кривошипа и значительно различаются. Если полученное в результате решения уравнения (17) значение d отличается от требуемого значения, в процедуре предусмотрена возможность его корректировки. Для этого следует изменить величину коэффициента r в формуле (13), проанализировав, как следует его изменять для увеличения или уменьшения d. После достижения необходимого значения d следует принять окончательное решение о месте установки маховика в результате оценки его габаритов и массы, что требуется для определения параметров, необходимых для выбора редуктора. В процедуре предусмотрено определение массива значений приведенного к кривошипу момента двигателя по формуле
а также углового ускорения кривошипа по формуле
где массив После завершения работы рассматриваемой процедуры следует с помощью процедуры Grafik вывести на экран графики После этого необходимо подобрать редуктор, для чего использовать соответствующую базу данных. Редуктор следует подобрать по величине передаточного отношения привода, выписанного вами с экрана дисплея, а также по величине максимального вращающего момента на выходном валу редуктора, который зависит от места установки маховика. Если маховик установлен на валу двигателя, то в качестве максимального момента следует принять 11 КИНЕМАТИЧЕСКИЙ АНАЛИЗ МЕХАНИЗМА При кинематическом анализе определяют линейные и угловые скорости элементов механизма, если это необходимо по условию выполняемого расчета, и аналогичные ускорения, необходимые для силового расчета. При известных значениях w1 и e1 кривошипа, а также передаточных функций механизма, кинематические параметры элементов механизма для различных положений кривошипа могут быть определены по следующим формулам. Угловая скорость и угловое ускорение i -го звена:
Проекции скорости и ускорения произвольной точки i -го звена:
Модули скорости и ускорения:
12 СИЛОВОЙ РАСЧЕТ МЕХАНИЗМА В результате силового расчета следует определить усилия, действующие на звенья механизма, и реакции в кинематических парах, что позволит определить продольные и поперечные усилия, а также изгибающие моменты в звеньях, необходимые для расчетаихна прочность, рассчитать подшипниковые узлы, а также направляющие при относительном поступательном движении звеньев. Результаты силового расчета позволяют оценить потери на трение в механизме, а следовательно, его КПД. На звенья механизма могут действовать следующие силы: - силы технологического (производственного) сопротивления - моменты технологического сопротивления Мi приложенные к i -м звеньям; - силы тяжести звеньев, приложенные в центрах масс звеньев, проекции которых
где ускорение g=9,81 м/с2. К этим силам, в соответствии с принципом Даламбера, следует добавить силы инерции звеньев механизма, которые для каждого звена в общем случае приводятся к главному вектору Фi и главному моменту - проекции главного вектора сил инерции:
- главный момент сил инерции
После формирования массивов сил и моментов сил инерции следует проверить правильность динамического анализа и определенных массивов. Для этого необходимо использовать общее уравнение динамики (принцип Лагранжа-Даламбера) для всего механизма в форме
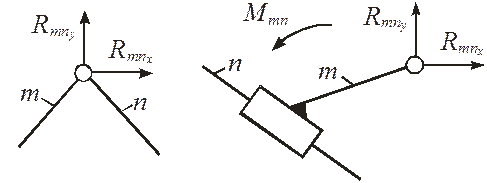
где Выражение (33) в программе идентифицировано как Pogr[i]. Значение погрешности для различных В противном случае следует отыскать допущенную ошибку и только после этого продолжить работу над программой. Методика отыскания допущенных ошибок изложена в конце этого раздела. Разложение реакций в кинематических парахпоказано на рис. 14.
Рисунок 14 – Реакции во вращательной и поступательной кинематических парах Реакцию в поступательной паре целесообразно привести к точке, совпадающей с осью вращательной пары, координаты которой определены в результате расчета, как это показано на рис. 14. Tак как реакция в поступательной паре перпендикулярна направляющей, то ее проекции связаны выражением
Силовой расчет рычажного механизма осуществляется последовательно по группам Ассура, начиная с той, которая соединена с остальной частью механизма двумя кинематическими парами. Для определения искомых реакций следует записать 6 уравнений равновесия. Среди этих уравнений могут быть уравнения в виде суммы проекций сил, приложенных к одному или обоим звеньям, на координатные оси или в виде суммы моментов приложенных сил относительно какой-либо точки. Если сила приложена в точке В и задана проекциями, то ее момент относительно точки А следует определять по теореме Вариньона:
При записи уравнений равновесия следует стремиться к тому, чтобы очередное уравнение содержало всего одну неизвестную. Рассмотрим методику записи уравнений равновесия на примере группы второго вида (рис. 15). Условимся реакции во внешних кинематических парах записывать с буквенными индексами, так как заранее неизвестны номера звеньев, к которым присоединяется эта группа Ассура. При этом предполагается, что эти реакции приложены со стороны отброшенной части механизма к звеньям рассматриваемой группы Ассура. Условимся также проекции всех сил изображать обязательно в положительном направлении без соблюдения масштаба, кроме сил тяжести, направляемых вертикально вниз.
Рисунок 15 – Группа Ассура второго вида с приложенными силами Моменты следует изображать направленными против часовой стрелки (положительное направление). При этом следует иметь в виду, что действительные значения этих величин определяются при работе программы. 1)
Из этого уравнения можно определить Мn. 2)
Учитывая, что 3)
Отсюда определяется 4)
Отсюда определяется 5)
Из этого уравнения можно определить 6) Из этого уравнения можно определить
При выполнении силового расчета следует использовать стандартные процедуры. Во всех этих процедурах в качестве входных параметров принимаются координаты осей кинематических пар, обозначенных на их схемах и углы направляющих. Кроме этого: Mс2, Mс3 - моменты сопротивления, приложенные ко второму и третьему звену; P2х, P2у, P3х, P3у - проекции внешних сил, приложенных к этим звеньям; Xk2, Yk2, Xk3, Yk3 - координаты точек приложения внешних сил; Mf2, Mf3 - моменты сил инерции звеньев; F2x, F2y, F3x, F3y - проекции сил инерции звеньев; Xs2, Ys2, Xs3, Ys3 - координаты центров масс звеньев. Выходными параметрами процедур являются реакции, представленные на схемах соответствующих структурных групп. Все эти процедуры входят в модуль TMM3m.tpu. Описание процедуры для расчета группы Ассура второго вида.
Sila2 (G2у, G3y: Real; var Xа, Yа, Xb, Yb, Fing, { входные параметры } Mc2, Xk2, Yk2, P2x, P2y, Mf2, Xs2, Ys2, F2x, F2y, Mc3, Xk3, Yk3, P3x, P3y, Mf3, Xs3, Ys3, F3x, F3y, RAx, RAy, R32x, R32y, Rnx, Rny, Mn: Massiv); { выходные параметры }
Ниже приводится целесообразная последовательность записи уравнений равновесия и описание стандартных процедур для остальных видов групп Ассура. При этом на схемах условно показаны только искомые реакции.
|
||||||||||||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 314; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.253.199 (0.01 с.) |

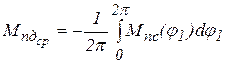 . (7)
. (7)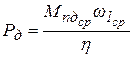 , (8)
, (8) - средняя угловая скорость кривошипа,
- средняя угловая скорость кривошипа,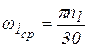 . (9)
. (9)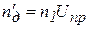 . (10)
. (10) , а номинальная мощность Pн была ближайшей большей или незначительно меньшей (на 10…15%) потребной мощности Рд. Для выбора электродвигателя следует использовать процедуру Motor, которая включена в модуль Dinamika.tpu.
, а номинальная мощность Pн была ближайшей большей или незначительно меньшей (на 10…15%) потребной мощности Рд. Для выбора электродвигателя следует использовать процедуру Motor, которая включена в модуль Dinamika.tpu. ;
;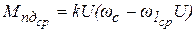 ,
, , (12)
, (12)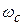 ,
, 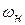 - синхронная и номинальная угловые скорости ротора:
- синхронная и номинальная угловые скорости ротора: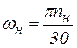 ,
, 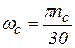 .
. , (13)
, (13)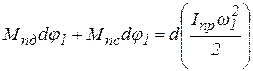 , (14)
, (14)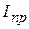 - приведенный к кривошипу момент инерции механизма,
- приведенный к кривошипу момент инерции механизма, , (15)
, (15)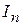 - переменная составляющая приведенного момента, определенная по формуле (5);
- переменная составляющая приведенного момента, определенная по формуле (5); - искомая функция угловой скорости кривошипа от его угла поворота
- искомая функция угловой скорости кривошипа от его угла поворота 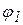 .
. . (16)
. (16)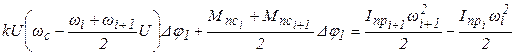 . (17)
. (17)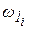 для i -гo положения кривошипа, из уравнения (17) можно определить
для i -гo положения кривошипа, из уравнения (17) можно определить 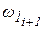 для (i+1) -го положения кривошипа. Поэтому сначала следует для начального положения кривошипа задаться величиной угловой скорости
для (i+1) -го положения кривошипа. Поэтому сначала следует для начального положения кривошипа задаться величиной угловой скорости 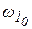 (в процедуре Оm10), желательно близкой к
(в процедуре Оm10), желательно близкой к 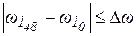 , (18)
, (18)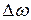 - заранее заданная малая величина, определяющая точность полученного решения. В рассматриваемой процедуре
- заранее заданная малая величина, определяющая точность полученного решения. В рассматриваемой процедуре 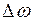 =0,001 рад/с.
=0,001 рад/с. и расчет продолжается до выполнения этого условия.
и расчет продолжается до выполнения этого условия.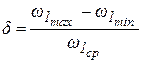
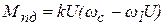 , (19)
, (19)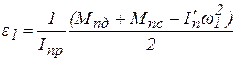 , (20)
, (20) рассчитан по формуле (6).
рассчитан по формуле (6).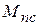 ,
, 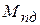 и
и 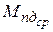 и выполнить качественную оценку правильности полученных результатов: площади под этими кривыми должны быть одинаковыми. На экран следует также вывести графики
и выполнить качественную оценку правильности полученных результатов: площади под этими кривыми должны быть одинаковыми. На экран следует также вывести графики 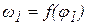 ,
, 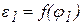 и
и  и провести их анализ. Если максимальные значения w1 и e1 окажутся существенно различающимися, целесообразно ввести дополнительное масштабирование, разделив или умножив соответствующий массив на подходящий коэффициент. Кроме того, с помощью процедуры TestPF следуeт протестировать
и провести их анализ. Если максимальные значения w1 и e1 окажутся существенно различающимися, целесообразно ввести дополнительное масштабирование, разделив или умножив соответствующий массив на подходящий коэффициент. Кроме того, с помощью процедуры TestPF следуeт протестировать 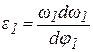 , то в качестве входных параметров тестовой процедуры следует принять:
, то в качестве входных параметров тестовой процедуры следует принять:  , а если на валу кривошипа, то
, а если на валу кривошипа, то 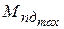 .Может оказаться, что передаточное отношение стандартного редуктора отличается от требуемого. Тогда необходимо подкорректировать частоту вращения кривошипа и повторить динамический анализ механизма.
.Может оказаться, что передаточное отношение стандартного редуктора отличается от требуемого. Тогда необходимо подкорректировать частоту вращения кривошипа и повторить динамический анализ механизма.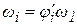 ; (21)
; (21)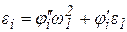 . (22)
. (22)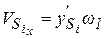 ; (23)
; (23)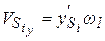 ; (24)
; (24) ; (25)
; (25)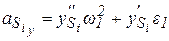 . (26)
. (26)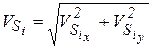 ; (27)
; (27)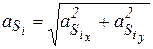 . (28)
. (28)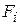 , приложенные в точке K i -го звена;
, приложенные в точке K i -го звена;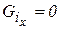 ;
; 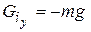 , (29)
, (29)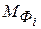 , и определяются по следующим формулам:
, и определяются по следующим формулам: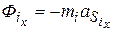 , (30)
, (30)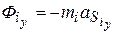 ; (31)
; (31)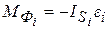 . (32)
. (32)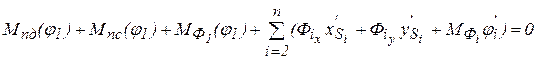 , (33)
, (33)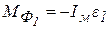 .
.
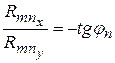 . (34)
. (34)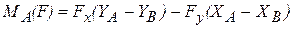 . (35)
. (35)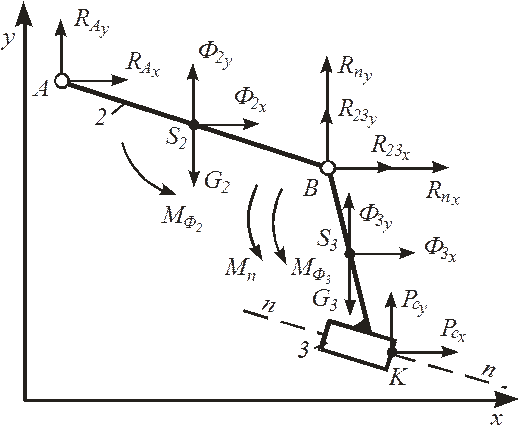
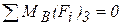 :
: (36)
(36)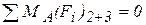 :
: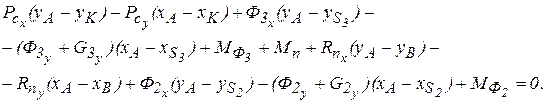 (37)
(37)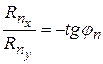 , из этого выражения можно определить
, из этого выражения можно определить  и
и 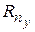 .
.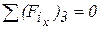 :
: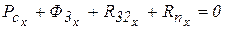 . (38)
. (38) .
.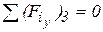 :
: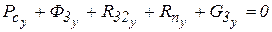 . (39)
. (39)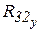 .
.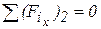 :
: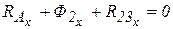 . (40)
. (40)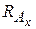 учитывая, что
учитывая, что 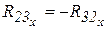 .
.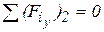 :
: 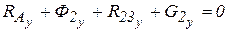 . (41)
. (41)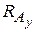 учитывая, что
учитывая, что .
.


