
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Донбасская государственная машиностроительнаяСодержание книги
Поиск на нашем сайте
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ ДОНБАССКАЯ ГОСУДАРСТВЕННАЯ МАШИНОСТРОИТЕЛЬНАЯ АКАДЕМИЯ
кафедра ОКММ
КОМПЛЕКСНЫЙ РАСЧЕТ РЫЧАЖНОГО МЕХАНИЗМА С ПОМОЩЬЮ ПЭВМ
Методические указания к изучению дисциплин
«Теория механизмов и машин», «Прикладная механика и основы конструирования», «Расчет и моделирование механических систем»
УДК 621.01
Комплексный расчет рычажного механизма с помощью ПЭВМ: Методические указания к изучению дисциплин «Теория механизмов и машин», «Прикладная механика и основы конструирования», «Расчет и моделирование механических систем» / Владимиров Э.А., Шоленинов В.Е., Чоста Н.В, - Краматорск: ДГМА, 2007. – 60 с.
Содержатся методические указания по выполнению комплексного расчета рычажного механизма с помощью ПЭВМ. Даны рекомендации по разработке программы для персонального компьютера на языке Turbo Pascal на базе использования аналитических методов расчета и графических средств программирования. Методика предполагает сочетание самостоятельной разработки студентом отдельных фрагментов программы с использованием стандартных процедур, разработанных на кафедре основ конструирования механизмов и машин. Большое внимание уделяется контролю правильности полученных результатов.
Составители Э.А. Владимиров, доц., В.Е. Шоленинов, асс.
Ответственный за выпуск С.Г. Карнаух, доц.
СОДЕРЖАНИЕ
Введение..................................................................................................... 4 1 Исходные данные для расчета механизма............................................. 4 2 Этапы расчета рычажного механизма................................................... 4 3 Структурный анализ механизма............................................................ 5 4 Техническое и программное обеспечение проектирования.................. 6 5 Структура программы........................................................................... 6 6 Стандартные процедуры для расчета структурных элементов........... 13 6.1 Передаточные функции кривошипа................................................ 15 6.2 Передаточные функции произвольной точки звена....................... 16 6.3 Передаточные функции группы Асcура первого вида.................. 17 6.4 Передаточные функции группы Асcура второго вида.................. 18
6.5 Передаточные функции группы Асcура третьего вида................. 19 6.6 Передаточные функции группы Асcура четвертого вида............. 20 6.7 Передаточные функции группы Асcура пятого вида.................... 21 6.8 Пример проектирования гиперболической лемнискаты Баутса.... 22 7 Контроль определения передаточных функций.................................... 26 8 Определение параметров динамической модели механизма................ 31 9 Выбор электродвигателя для привода механизма................................ 35 10 Подбор маховика и определение закона движения начального звена 38 11 Кинематический анализ механизма..................................................... 43 12 Силовой расчет механизма.................................................................. 44 12.1 Силовой расчет группы Ассура первого вида............................. 49 12.2 Силовой расчет группы Ассура третьего вида............................ 50 12.3 Силовой расчет группы Ассура четвертого вида........................ 51 12.4 Силовой расчет группы Ассура пятого вида............................... 52 13 Порядок оформления и представления отчетной документации по курсовому проекту................................................................................................... 58 14 Комплексный расчет гидравлического пресса.................................... Перечень ссылок........................................................................................ 59 ВВЕДЕНИЕ
Настоящие методические указания содержат рекомендации по выполнению раздела инженерного расчета рычажного механизма второго класса для получения исходных данных, которые используют при расчете деталей механизма и привода на прочность. Этот раздел инженерного расчета является содержанием выполняемого вами курсового проекта.
ИСХОДНЫЕ ДАННЫЕ ДЛЯ РАСЧЕТА МЕХАНИЗМА
Исходными данными для проектирования рычажного механизма являются: - структурная схема механизма; - координаты неподвижных осей вращательных кинематических пар и неподвижных направляющих, мм; - длины звеньев, мм; - положение центров масс звеньев и мест приложения внешних сил; - массы звеньев и их моменты инерции; - силы технологического сопротивления в функции от положения выходного звена; - частота вращения кривошипа, об/мин.
ПРОЕКТИРОВАНИЯ
Для выполнения курсового проекта необходимо иметь: - систему Turbo Pascal, включающую файлы Turbo.exe, Turbo.tpl, Graph.tpu и EgaVga.bgi, общим объемом около 200 КВ;
- исходную программу Mechan1.pas; - модули MPF.tpu, Dinamika.tpu и TMM3m.tpu, содержащие стандартные процедуры общим объемом около 160 КВ. Необходимо знать основы программирования на языке Turbo Pascal, а также основные приемы работы с системой Turbo Pascal [2].
5 СТРУКТУРА ПРОГРАММЫ
Структуру программы рассмотрим на примере исходной программы Mechan1.pas. Ниже приводится сокращенный текст программы, содержащий подробные комментарии, которых нет в исходном файле. Эти комментарии набраны курсивом и заключены в фигурные скобки.
Program Mechan; { Имя программы } Uses Crt, Graph, MPF, Dinamika, TMM3m; { Перечень модулей } Const m=48; { Описание констант } { Эта константа равна числу интервалов, на которое делится траектория точки А кривошипа. Поэтому все расчеты будут проводиться для m+1 положений кривошипа } Var Xo, Yo, LOA, FiOA0g, dFi, m2, Is2: Real; { Описание переменных } { В описание переменных включены имена, которые, вероятнее всего, будут вами использованы при разработке программы. Их значения разъясняются в процессе рассмотрения программы и используемых процедур. Описание переменных Вы будете дополнять при разработке программы } { Целесообразно принять следующую систему описания имен переменных: Xs2, Ys2 – координаты точки S, принадлежащей звену 2; Xs2_1, Ys2_1 - передаточные функции первого порядка (ПФ1) точки S2; Xs2_2, Ys2_2 - передаточные функции второго порядка (ПФ2) точки S2; FiABg, FiABr - угол, образуемый осью звена АВ с положительным направлением оси абсцисс, в градусах и радианах (угловая ПФ0 звена); FiAB_1, FiAB_2 - угловые ПФ1 и ПФ2 звена АВ } Var Xa, Ya, Xa_1, Ya_1, Xa_2, Ya_2: Massiv; { Описание ПФ т. А } Var FiABg, FiABr, FiAB_1, FiAB_2: Massiv; { Описание ПФ угла АВ } Var G2y, G3y, G4y, G5y: Real; { Описание сил тяжести } { РАЗДЕЛ ОПЕРАТОРОВ } Begin Driver:=Detect; { Инициализация графики } InitGraph (Driver, Mode, ’’); SetBKcolor(7); { ОПРЕДЕЛЕНИЕ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ МЕХАНИЗМА } For i:=1 to m+1 Do Begin { Цикл для расчета значений передаточных функций для 49 положений кривошипа (полный оборот с угловым шагом 7,5 градуса) } СlearDevice; { Очистка графического экрана } Str (i:2, StrVar); { РАСЧЕТ КРИВОШИПА } { Присвоение значения исходных данных. Координаты и длины - в миллиметрах, углы в градусах } XO:=-700; { Координаты оси кривошипа } YO:=0; { Координаты оси вращения кривошипа XO и YO следует выбрать с учетом рационального расположения изображения механизма на экране, имея в виду, что начало координат находится в центре экрана, положительное направление оси абсцисс вправо, а оси ординат - вверх. Начальный угол кривошипа FiOA0g сначала можно принять произвольно с тем, чтобы в дальнейшем присвоить ему рациональное значение, например, что чаще всего и требуется, соответствующее началу рабочего хода выходного звена } LOA:=60; { Длина кривошипа, мм } FiOAg:=97.05; { Начальный угол кривошипа, град } Fi:=360/m; { Угол поворота кривошипа, град } dFir:=2*pi/m; { Угол поворота кривошипа, рад } jk:=1; { Признак направления вращения кривошипа } q:=1; { Признак отображения механизма } Mas:=2.5; { Масштабный коэффициент } Fioag[i]:=Fioa0g+dFi*(i-1)*jk; { Расчет текущего угла кривошипа } Str (Fioag[i]:8:4, StrVar); SetColor (15); { Обращение к процедуре, рассчитывающей передаточные функции точки А кривошипа и рисующей его изображение. Эта процедура содержится в модуле MPF.tpu } Kriv (Xo, Yo, Loa, Fioag[i], q, jk, Mas, { Входные данные } Xa[i], Ya[i], Xa_1[i], Ya_1[i], Xa_2[i], Ya_2[i]); { Выходные данные } { С описанием процедуры Kriv Bы сможете ознакомиться в разделе 6 } lc:=75; Ori:=1; Opora (Xo, Yo, l, Mas, q, Ori); { Рисование опоры кривошипа }
{ С описанием процедуры OporaВы сможете ознакомиться в разделе 6 } { Исходная программа Mechan1.pas готова к работе. В результате запуска программы в среде Turbo Pascal Вы получите на экране изображение кривошипа, положение которого можно изменять с шагом 7,5 градусов при нажатии на клавишу ПРОБЕЛ. Кроме этого, Вы сможете просмотреть графики передаточных функций точки А кривошипа и результаты их тестирования. Используемые с этой целью процедуры Grafik и TestPF вызываются после завершения цикла расчета передаточных функций и описаны в разделе 7 } { После просмотра работы исходного варианта программы следует продолжить ее разработку, начав с введения коррективов в исходные данные в соответствии с параметрами рассчитываемого Вами механизма } { РАСЧЕТ ПЕРВОЙ ПРИСОЕДИНЕННОЙ ГРУППЫ АССУРА } { Прежде чем перейти к присоединению структурных групп в соответствии с формулой строения механизма, следует ознакомиться с содержанием процедур для определения передаточных функций элементов механизма и порядком их использования, что изложено в разделе 6 } { РАСЧЕТ ВТОРОЙ ПРИСОЕДИНЕННОЙ ГРУППЫ АССУРА } ReadKey; { Обеспечивает пошаговый режим просмотра изображения } End; { Завершение цикла расчета передаточных функций механизма } CloseGraph; { Переход в текстовый режим } { ТЕСТИРОВАНИЕ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ } { Порядок тестирования изложен в разделе 7 } TestPF (m, Xa, Xa_1, Xa_2, ‘Xa’); Grafik (m+1, FiOAg, Xa, Xa_1, Xa_2, ’Xa’, ’Xa_1’, ’Xa_2’); TestPF (m, Ya, Ya_1, Ya_2, ‘Ya’); Grafik (m+1, FiOAg, Ya, Ya_1, Ya_2, ’Ya’, ’Ya_1’, ’Ya_2’); { ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ДИНАМИЧЕСКОЙ МОДЕЛИ } m2:=100; { Массы звеньев } m3:=200; m4:=300; m5:=1200; Is2:=0.2; { Моменты инерций звеньев } Is3:=0.5; Is4:=0.9; G2y:=-m2*g; { Силы тяжести звеньев } G3y:=-m3*g; G4y:=-m4*g; G5y:=-m5*g; { В приводимых ниже выражениях следует убрать лишние или добавить недостающие для Вашего механизма слагаемые. В частности, необходимо сформировать массив значений силы технологического сопротивления. Деление некоторых слагаемых на числовой коэффициент объясняется тем, что передаточные функции вводятся в эти формулы в миллиметрах, а результаты нам необходимо получить в единицах, содержащих метры } For i:=1 to m+1 Do Begin Mnc[i]:= (G2y*Ys2_1[i]+ { Расчет приведенного момента внешних сил } G3y*Ys3_1[i]+ G4y*Ys4_1[i]+ G5y*Ys5_1[i])/1000; Ip2[i]:=(m2*(sqr(Xs2_1[i])+sqr(Ys2_1[i]))+ m3*(sqr(Xs3_1[i])+sqr(Ys3_1[i]))+ m4*(sqr(Xs4_1[i])+sqr(Ys4_1[i]))+ m5*(sqr(Xs5_1[i])+sqr(Ys5_1[i]))/1000000+ Is2*sqr(FiAB_1[i]); Ip2_1[i]:= 2*(m2*(Xs2_1[i]*Xs2_2[i]+Ys2_1[i]*Ys2_2[i])+ m3*(Xs3_1[i]*Xs3_2[i]+Ys3_1[i]*Ys3_2[i])+ m4*(Xs4_1[i]*Xs4_2[i]+Ys4_1[i]*Ys4_2[i])+ m5*(Xs5_1[i]*Xs5_2[i]+Ys5_1[i]*Ys5_2[i]))/1000000+ 2*Is2*FiAB_1[i]*FiAB_2[i]; { Порядок определения приведенного момента внешних сил Мпс, переменной части приведенного момента инерции механизма Ip2 и ее производной Ip2_1 по обобщенной координате изложен в разделе 8 }
End; { Завершение цикла расчета динамических параметров механизма } { ВЫБОР ЭЛЕКТРОДВИГАТЕЛЯ ДЛЯ ПРИВОДА МЕХАНИЗМА } { Порядок выбора электродвигателя для привода изложен в разделе 9 } { ОПРЕДЕЛЕНИЕ ЗАКОНА ДВИЖЕНИЯ КРИВОШИПА } { Методика решения дифференциального уравнения движения начального звена механизма и определения момента инерции маховика, а также порядок использования соответствующей процедуры изложены в разделе 10 } { ОПРЕДЕЛЕНИЕ СИЛ И МОМЕНТОВ СИЛ ИНЕРЦИИ } { В приводимых ниже операторах следует убрать лишние или добавить недостающие для Вашего механизма выражения. Проекции ускорений по этим формулам вычисляются в метрах на секунду в квадрате } For i:=1 to m+1 Do Begin as2x:=(Xs2_2[i]*sqr(Om1[i])+Xs2_1[i]*e1[i])/1000; { Ускорения точек } as2y:=(Ys2_2[i]*sqr(Om1[i])+Ys2_1[i]*e1[i])/1000; as3x:=(Xs3_2[i]*sqr(Om1[i])+Xs3_1[i]*e1[i])/1000; as3y:=(Ys3_2[i]*sqr(Om1[i])+Ys3_1[i]*e1[i])/1000; as4x:=(Xs4_2[i]*sqr(Om1[i])+Xs4_1[i]*e1[i])/1000; as4y:=(Ys4_2[i]*sqr(Om1[i])+Ys4_1[i]*e1[i])/1000; as5x:=(Xs5_2[i]*sqr(Om1[i])+Xs5_1[i]*e1[i])/1000; as5y:=(Ys5_2[i]*sqr(Om1[i])+Ys5_1[i]*e1[i])/1000; e2:=FiAB_2[i]*sqr(Om1[i])+FiAB_1[i]*e1[i]; { Угловые у скорения звеньев } F2x[i]:=-m2*as2x; { Силы инерций звеньев } F2y[i]:=-m2*as2y; F3x[i]:=-m3*as3x; F3y[i]:=-m3*as3y; F4x[i]:=-m4*as4x; F4y[i]:=-m4*as4y; F5x[i]:=-m5*as5x; F5y[i]:=-m5*as5y; Mf1[i]:=-Ip1*e1[i]; { Моменты сил инерций звеньев } Mf2[i]:=-Is2*e2; End; { Проверка правильности динамического анализа механизма и значений сил и моментов сил инерции. Порядок проверки изложен в разделе 12. В приведенном ниже выражении следует убрать лишние или добавить недостающие для Вашего механизма слагаемые } For i:=1 to m+1 Do Pogr1[i]:=Mpd[i] + Mnc[i] + Mf1[i]+ (F2x[i]*Xs2_1[i] + F2y[i]*Ys2_1[i] + F3x[i]*Xs3_1[i] + F3y[i]*Ys3_1[i] + F4x[i]*Xs4_1[i] + F4y[i]*Ys4_1[i] + F5x[i]*Xs5_1[i] + F5y[i]*Ys5_1[i])/1000 + Mf2[i]*FiAB_1[i]; Grafik (m+1, Fioag, Pogr1, zz, zz, ’Pogr1’, ’’, ’’); { СИЛОВОЙ РАСЧЕТ СТРУКТУРНЫХ ГРУПП АССУРА } { Следует ознакомиться с порядком силового расчета механизма, а также с методикой контроля его правильности, что изложено в разделе 12 } { Проверка правильности силового расчета структурной группы } { Силовой расчет остальных структурных групп с проверкой его правильности } { ГЛОБАЛЬНАЯ ПРОВЕРКА РАСЧЕТА } { Методика глобальной проверки расчета изложена в разделе 12 } For i:=1 to n+1 Do PogrGlob[i]:=Mpd[i]+Mf1[i]+(R12x[i]*(Yo-Ya[i]-R12y[i]*(Xo-Xa[i]))/1000; Grafik (m+1, FiOAg, PogrGlob, zz, zz, ’PogrGlob’, ’’, ’’); { Вывод графиков реакций в кинематических парах, их годографов и графиков углов давления } End. { Конец программы } { Описание используемых процедур } { В конце исходной программы, записанной на дискете, приведены описания процедур, входящих в состав модулей MPF.tpu, Dinamika.tpu и TMM3m.tpu, что облегчает обращение к ним при разработке программы. Для этого необходимую процедуру следует выделить с помощью курсора, перенести в нужное место программы и вместо формальных параметров подставить фактические, убрав при этом обозначение типов переменных } 6 СТАНДАРТНЫЕ ПРОЦЕДУРЫ ДЛЯ РАСЧЕТА СТРУКТУРНЫХ ЭЛЕМЕНТОВ МЕХАНИЗМА
Стандартные процедуры для расчета передаточных функций структурных элементов рычажных механизмов разработаны на основе аналитических методов. ПФ0 представляют собой зависимости углов звеньев и координат характерных точек от геометрических параметров элементов внешних кинематических пар, полученных на основе простых геометрических соотношений. ПФ1 и ПФ2 получены посредством последовательного дифференцирования этих выражений по обобщенной координате. Так как эти выражения достаточно громоздкие, они не приводятся в настоящих указаниях. Принеобходимости с ними можно ознакомиться по методическим указаниям [3].
Имеющиеся на вашей дискете процедуры метрического анализа механизма позволяют не только рассчитать передаточные функции, но и получить на экране дисплея изображение соответствующего структурного элемента, что необходимо для контроля правильности работы программы, а также наглядного представления о работе механизма и его особенностях. Пример проектирования гиперболической лемнискаты Баутса
Рассмотрим фрагмент программы, в котором определяются передаточные функции кулисно-рычажного механизма Артоболевского для воспроизведения гиперболической лемнискаты Баутса, изображенного на рис. 9.
Рисунок 9 – Кулисно-рычажный механизм Артоболевского
При вращении кривошипа 1 точка D описывает лемнискату, изображение которой следует получить на экране дисплея. Формула строения механизма I(0, 1) → II(2, 3)1 → II(4, 5)3 → II(6, 7)2 . Рассмотрим план расчета механизма, основываясьна его формуле строения. Вначале, используя процедуру Kriv, следует определить параметры точки А кривошипа. После этого, используя процедуру Assur1, следует определить передаточные функции звеньев 2 и 3, а затем с помощью процедуры Point - передаточные функции точки В. На следующем этапе с помощью процедуры Assur3 следует определить передаточные функции кулисы 4, после чего с помощью процедуры Assur2 определить передаточные функции шатуна 6. В заключение с помощью процедуры Point следует определить параметры точки D и с помощью процедуры Track получить ее траекторию - лемнискату Баутса. В процессе разработки этого этапа программы следует использовать описания процедур, приведенные в конце исходной программы, в соответствии с рекомендациями. С целью упрощения замены формальных параметров фактическими в описании используемых процедур целесообразно вместо переменных, величина которых заведомо равна нулю (например, ПФ1 и ПФ2 неподвижных точек и неподвижных направляющих), подставлять переменную z=0 или просто 0. В качестве одного из результатов работы этого этапа программы на рис. 10 представлена копия экрана с изображением механизма и траектории точки D.
Рисунок 10 – Копия экрана с изображением механизма и участком траектории камня
Ниже приводится фрагмент кода программы для создания лемнискаты Баутса.
FiOAg0:=0; { Начальный угол поворота кривошипа } z:=0; For i:=1 To m+1 Do Begin { Цикл определения ПФ } ClearDevice; { Очистка графического экрана } jk:=1; FiOAg[i]:=FiOAg0+360/(m+1)*(i-1)*jk; { Угол поворота кривошипа }
{ КРИВОШИП } Xo:=0; { Координаты оси вращения кривошипа } Yo:=0; LOA:=500; { Длина кривошипа } q:=1; Mas:=8; { Масштабный коэффициент } Kriv (Xo, Yo, LOA, FiOAg[i], q, jk, Mas, Xa[i], Ya[i], Xa_1[i], Ya_1[i], Xa_2[i], Ya_2[i]);
{ ГРУППА 1-ГО ВИДА } Xc:=1000; { Координаты опоры – точки С } Yс:=0; LAB:=1000; { Длины звеньев группы } LCB:=LOA; If Ya[i]<=0 Then j1:=1 Else j1:=-1; { Это условие приходится вводить, чтобы четырехзвенник ОАВС всегда был антипараллелограммом } Assur1 (Xa[i], Ya[i], Xa_l[i], Ya_l[i], Xa_2[i], Ya[i]2, Xc, Yс, z, z, z, LAB, LCB, j1, q, Mas, FiABg[i], FiCBg[i], FiAB_1[i], FiCB_l[i], FiAB_2[i], FiCB_2[i]);
FiABr[i]:=FiABg[i]/180*pi; { Значения углов в радианах } FiCBr[i]:=FiCBg[i]/180*pi;
{ ОПРЕДЕЛЯЕМ ТОЧКУ В } r:=5; Point (Xa[i], Ya[i], Xa_1[i], Ya_l[i], Xа_2[i], Ya_2[i], FiABg[i], FiAB_1[i], FiAB_2[i], LAB, z, q, Mas, r, Xb[i], Yb[i], Xb_1[i], Yb_1[i], Xb_2[i], Yb_2[i]);
{ ГРУППА 3-ГО ВИДА } lcc: = 100; { Длина диагонали камня } Assur3 (Xb[i], Yb[i], Xb_1[i], Yb_1[i], Xb_2[i],Yb_2[i], Xо, Yо, z, z, z, z, z, z, Mas, lcc, q, Fikg[i], Fik_1[i], Fik_2[i]); Fikr[i]: = Fikg[i]/180*pi; { Значения углов в радианах }
{ ГРУППА 2-ГО ВИДА } LAD: =LOA; { Длины звеньев группы } j2: =1; { Признак сборки группы } { Здесь опущено условие изменения признака сборки группы 2-го вида, требуемое для получения всей лемнискаты } Assur2 (Xa[i], Ya[i], Xa_1[i], Ya_l[i], Xа_2[i], Ya_2[i], Xo, Yо, z, z. z, z, Fikg[i], Fik_1[i], Fik_2[i], Z, LAD, z, lcc, j2, q, Mas, FiADg[i], FiAD_1[i], FiAD_2[i]); FiADr[i]: = FiADg[i]/180*pi; { Значения углов в радианах }
{ ОПРЕДЕЛЯЕМ ТОЧКУ D } Point (Xa[i], Ya[i], Xa_1[i], Ya_l[i], Xа_2[i], Ya_2[i], FiADg[i], FiAD_1[i], FiAD_2[i], LAD, z, q, Mas, r, Xd[i], Yd[i], Xd_1[i], Yd_1[i],Xd_2[i], Yd_2[i]); k:=i; Track(k, q, Mas, Xd, Yd); { Рисуем траекторию точки D } End; { Конец цикла } 7 КОНТРОЛЬ ОПРЕДЕЛЕНИЯ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
Качественная оценка правильности определения ПФ0 элементов механизма осуществляется посредством наблюдения на экране изображения соответствующего структурного элементаи ихвзаимного расположения. При этом удобно контролировать правильность задания точек присоединения структурных элементов или направляющих, по которым они движутся, признака сборки структурной группы или знака задаваемого геометрического параметра, если он является алгебраической величиной. Количественная оценка ПФ0 может быть выполнена в результате построения кинематической схемы в масштабе методом засечек для одного или нескольких положений начального звена. Рассмотрим порядок построения кинематической схемы на примере механизма, изображенного на рис. 9. Известны координаты точки С и длины звеньев lOA, lAB, lCB, lAD. Сначала следует выбрать стандартную величину масштаба (например, 2:1, 1:1, 1:2 и т.д.) и вычислить масштабные значения координат точки С и длин звеньев. Выбрав на чертеже начало координат (точку О), следует по координатам xC и yC построить точку С. После этого для некоторого угла поворота кривошипа определить положение точки А. Угол, определяющий положение кривошипа, следует отсчитывать от положительного направления оси х против часовой стрелки. При этом угол кривошипа должен быть определен по формуле
где в качестве i принимается одно из значений от 1 до 48. В качестве начального угла кривошипа целесообразно принять угол, соответствующий началу рабочего хода, о чем более подробно смотри в начале раздела 8. После этого раствором циркуля, равным масштабным значениям длин звеньев lAB и lCB, сделать засечки из центров А и С и на их пересечении получить точку В. Углы, определяющие положение звеньев АВ и СВ, нужно измерить транспортиром, отсчитывая от прямой, проведенной параллельно оси х через начальную точку в обозначении звена, против часовой стрелки. После этого следует провести звено 4 и определить его угол наклона jOB. Далее необходимо из точки А сделать засечку радиусом lAD на оси звена 4, получить точку D и измерить угол jAD. После этого необходимо определить координаты всех характерных точек механизма (осей вращательных кинематических пар и центров масс звеньев). Результаты графических построении следует сравнить с результатами, полученными на базе аналитических методов в процессе работы программы. Для этого необходимо использовать процедуру Grafik. Описание процедуры: Grafik (m: Integer; OK, Y1, Y2, Y3: Massiv; S1, S2, S3: String), где OK – формальное имя обобщенной координаты, например, угла поворота кривошипа, являющегося абсциссой представляемых графиков; m - число значений элементов массивов, представляемых на экране; Y1, Y2, Y3 - формальные имена массивов, графики которых будут представлены на экране; S1, S2, S3 - формальные строковые переменные, служащие для идентификации графиков на экране. Поскольку все три графика строятся в одинаковом масштабе, целесообразно на экран выводить массивы, максимальные величины которых имеют одинаковый порядок, например передаточные функции точек механизма. В связи с этим при выводе на экран передаточных функций, характеризующих вращательное движение звеньев, углы следует выводить в радианах. Первый график представляется на экране зеленой линией, второй - красной и третий ‑ желтой. Кроме того, на экран выводится вертикальная линия, которая с помощью клавиш “” и “®” может перемещаться влево и вправо и занимать положение, соответствующее любому из m положений кривошипа. При этом на экран выводятся численные значения обобщенной координаты (например, угла, определяющего положение кривошипа), а также значения выводимых функций. На рис. 11 представлена копия экрана с изображением графиков для абсциссы точки D механизма. Здесь сплошная линия соответствует зеленой линии, штриховая – красной, а пунктирная – желтой. Установив вертикальную линию в положение, соответствующее построенной кинематической схеме, можно сравнить расчетное значение координаты со значением, полученным графическим методом.
Рисунок 11 – Графики передаточных функций камня
В случае их существенного различия (свыше 2…3 мм) сначала следует проконтролировать правильность построения кинематической схемы, а затем правильность обращения к процедуре, рассчитывающей этот параметр. При контроле угловых координат звеньев разница углов, определяемых аналитическим и графическим методами, не должна превышать 1 градуса. В программе необходимо предусмотреть вывод на экран передаточных функций всех звеньев и характерных точек механизма. При этом их вывод необходимо выполнять в той же последовательности, в какой они рассчитываются в программе. Это может существенно упростить отладку этого этапа программы. Так, для механизма, представленного на рис. 9, графики следует выводить в такой последовательности xA, yA, jAB, jCB, jOB, При этом нужно добиваться правильности анализируемого параметра и только после этого переходить к анализу следующего. В случае правильности ПФ0 рассматриваемого параметра с помощью выведенных на экран графиков можно дать качественную оценку правильности ПФ1 и ПФ2. Рассмотрим это на примере графиков, представленных на рис. 11. Эти графики связаны между собой операцией дифференцирования. При этом на интервале, где функция xD (сплошная линия) убывает, ее производная Для количественной оценки правильности передаточных функций следует использовать процедуру TestPF. В ее основу положен метод численного дифференцирования. Значения первой и второй производных функции в какой-либо точке можно определить, зная ее значение в этой и трех соседних точках справа и слева, взятых с одинаковым шагом Dj, по формулам:
Метод численного дифференцирования является менее точным, чем аналитический, однако расчеты показывают, что для достаточно плавных функций производные, найденные этими методами, отличаются весьма незначительно. На этом и основано применение рассматриваемой процедуры которая предусматривает ввод ПФ0, ПФ1 и ПФ2 какого-либо элемента механизма, расчет ПФ1 и ПФ2 по формулам (2) и (3) и сравнение передаточных функций, определенных двумя способами. Если разница этих величин не превышает 0,1%, аналитические значения передаточных функций можно считать правильными. В противном случае на экран выводятся значения передаточных функций длятех точек, где их разница превышает 0,1%. Если такая разница оказывается для всех положений начального звена, в программе, вероятнее всего, при обращении к соответствующей процедуре допущена ошибка, которую следует найти и устранить. Если же такая разница обнаруживается лишь отдельных точках кривой, характеризуемых резким изменением передаточных функций, их значения следует считать правильными. В некоторых случаях может наблюдаться разница значений передаточных функций, найденных двумя методами, в семи последовательных точках. Это возможно, когда функция претерпевает разрыв, например, для графика угла звена механизма, где величина разрыва первого рода может равняться периоду тригонометрической функции, используемой для определения угла наклона звена. Этот разрыв можно наблюдать на графике ПФ0, после чего следует принять меры по его устранению. Значения же ПФ1 и ПФ2 следует считать правильными. Описание процедуры: TestPF (m: Integer; Yf, Yf1, Yf2: Massiv; StrYf: String), где m - число значений элементов массива; Yf, Yf1, Yf2 - формальные имена передаточных функций, определенных аналитически; StrYf - формальная строковая переменная, идентифицирующая тестируемый параметр. Шаг численного дифференцирования При тестировании углов, определяющих положение звеньев, значение ПФ0 следует вводить в радианах. Тестирование обязательно для всех метрических параметров механизма, так как значения всех передаточных функций будут использованы в последующих расчетах. 8 ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ДИНАМИЧЕСКОЙ МОДЕЛИ МЕХАНИЗМА
На следующем этапе программы вычисляются величины, необходимые для выбора двигателя и определения закона движения начального звена механизма: приведенный момент внешних сил, действующих на звенья механизма, а также переменная составляющая приведенного момента инерции звеньев механизма и ее производная. В состав внешних активных сил входят силы тяжести звеньев, а также силы или моменты сил технологического сопротивления. Обычно в технологических машинах силы сопротивления действуют лишь на отдельном участке перемещения выходного звена, который называется рабочим ходом. Для более удобного представления графической информации на экране дисплея целесообразно в качестве начального принять положение кривошипа При определении угла кривошипа, соответствующего началу рабочего хода, следует иметь в виду, что выходное звено занимает при этом крайнее положение и его ПФ1 равна нулю. Методика определения такого угла кривошипа следующая. В первом приближении его следует принять по графику ПФ1 равным значению левой границы интервала, на котором ПФ1 меняет знак. Присвоив это значение переменной FiOA0g и уменьшив шаг dFi, следует найти новое значение начального угла кривошипа. Такие уточнения следует продолжить до тех пор, пока величина ПФ1 на левой границе интервала изменения знака не окажется по модулю меньшей 0,0005. Это значение обобщенной координаты и будет соответствовать началу рабочего хода. Присвоив после этого шагу dFi первоначальное значение, следует продолжить разработку программы. При последующей работе над программой с целью сокращения времениее отладки параметру q можно присвоить значение 0 (на экран не будет выводиться изображение механизма) и с помощью скобок { } отключить процедуры Grafik и TestPF. Приведенный момент внешних сил без учета момента двигателя может быть определен для любого положения механизма по формуле
где
Мi - внешний момент, приложенный к i -му звену;
Суммирование проводится по всем подвижным звеньям механизма, кроме кривошипа. В исходной программе приведена эта формула, однако ее следует подкорректировать для рассчитываемого механизма. Особое внимание следует уделить формированию массивов значений проекций сил или моментов технологического сопротивления. В качестве примера рассмотрим задание силы технологического сопротивления для механизма, у которого выходное звено (ползун), обозначаемое буквой D, совершает возвратно-поступательное движение параллельно оси абсцисс. Рабочий ход совершается при движении ползуна справа налево. График зависимости силы сопротивления от положения ползуна на рабочем ходу показан на рис. 12. При холостом ходе сила сопротивления равна нулю.
Рисунок 12 – График силы сопротивления На этом графике:
Тогда на отдельных участках рабочего хода задание силы сопротивления при при 0,2 < при 0,4< пpи 0,7< при холостом ходе: В этом случае фрагмент программы для определения силы технологического сопротивления при 49 расчетных положениях кривошипа может иметь следующий вид. Заметим, что в этом фрагменте рабочий и холостой ход различаются по знаку ПФ1 ползуна. For i:=1 to 49 Do Begin if XD[i]>XDmax Then XDmax:=XD[i]; if XD[i]<XDmin Then XDmin:=XD[i]; End; {For} SDmax:=XDmax-XDmin; Pcmax:=10000; For i:=1 to 49 Do Begin S_[i]]:=(XDmax-XD[i])/SDmax; if S_[i]<=0.2 Then Pcx[i]:=0; if (S_[i]>0.2) And (S_[i]<=0.4) Then Pсх[i]:=Pcmax/0.2*(s_[i]-0.2); if (S_[i]>0.4) And (S_[i]<=0.7) Then Pcx[i]:=Pcmax; if (S_[i]>0.7) Then Pcх[i]:=Pcmax/0.3*(1-s_[i]); if Xd_1[i]>0 Then Pcx[i]:=0; End; {For} Дл
|
||||||||||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 218; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.149.14 (0.018 с.) |

 Краматорск 2007
Краматорск 2007


 , (1)
, (1)
 ,
, 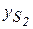 ,
,  ,
, 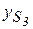 , xB, yB,
, xB, yB, ,
,  , jAD,
, jAD,  ,
,  , xD, yD.
, xD, yD.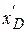 (штриховая линия) отрицательна, а на интервале возрастания x D производная положительна. Точке экстремума графика хD соответствует значение
(штриховая линия) отрицательна, а на интервале возрастания x D производная положительна. Точке экстремума графика хD соответствует значение  = 0. Аналогичную связь можно обнаружить и между графиками
= 0. Аналогичную связь можно обнаружить и между графиками  (пунктирная линия). Следует также обратить внимание на тот факт, что абсцисса, где
(пунктирная линия). Следует также обратить внимание на тот факт, что абсцисса, где  (2)
(2) . (3)
. (3) .
. соответствующее началу рабочею хода. Это изменение следует внести в программу и вновь просмотреть все графики передаточных функций элементов механизма.
соответствующее началу рабочею хода. Это изменение следует внести в программу и вновь просмотреть все графики передаточных функций элементов механизма.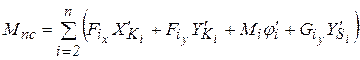 , (4)
, (4)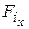 ,
,  - проекции внешней силы, приложенной в точке Ki -го звена;
- проекции внешней силы, приложенной в точке Ki -го звена; ,
, 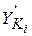 - ПФ1 точки Ki;
- ПФ1 точки Ki; - угловая ПФ1 i -гo звена;
- угловая ПФ1 i -гo звена; - проекция силы тяжести i -гo звена;
- проекция силы тяжести i -гo звена; - ПФ1 центра масс i -гo звена.
- ПФ1 центра масс i -гo звена.
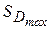 - рабочий ход ползуна,
- рабочий ход ползуна,  ;
; - текущее значение перемещения ползуна,
- текущее значение перемещения ползуна,  ;
; - максимальное значение силы технологического сопротивления, задаваемое в исходных данных на проектирование.
- максимальное значение силы технологического сопротивления, задаваемое в исходных данных на проектирование.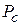 может быть описано следующими выражениями:
может быть описано следующими выражениями: £ 0,2:
£ 0,2: 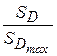 £ 0,4:
£ 0,4:  (
(


