Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Xc, Yc, z, z, z, 90, z, z, 400, Lbd, z, lcc, j2, q, Mas,Содержание книги
Поиск на нашем сайте
FiBDg[i], FiBD_1[i], FiBD_2[i]); { Выходные } FiBDr[i]:=FiBDg[i]/180*pi; { Пересчёт из градусной меры в радианную } { Обращение к процедурам Point для определения ПФ точки D ползуна, а также центра масс шатуна S4 в предположении, что центр масс лежит на его средине } Point (Xb[i], Yb[i], Xb_1[i], Yb_1[i], Xb_2[i], Yb_2[i], { Входные } FiBDg[i], FiBD_1[i], FiBD_2[i], LBD, z, q, Mas, 3, Xd[i], Yd[i], Xd_1[i], Yd_1[i], Xd_2[i], Yd_2[i]); { Выходные } Yd_[i]:=Yd[i]/1000; Point (Xb[i], Yb[i], Xb_1[i], Yb_1[i], Xb_2[i], Yb_2[i], { Входные } FiBDg[i], FiBD_1[i], FiBD_2[i], Lbd/2, z, q, Mas, 3, Xs4[i], Ys4[i], Xs4_1[i], Ys4_1[i], Xs4_2[i], Ys4_2[i]); { Выходные } Xs4_[i]:=Xs4[i]/1000; Ys4_[i]:=Ys4[i]/1000; ReadKey; { Продолжение работы программы после нажатия клавиши } X1[i+1]:=X1[i]+jp*dX1; { Переход к следующей ОК } End; { For } { Завершение цикла } ClearDevice; { Очистка графического экрана } CloseGraph; { Выход из графического режим а }
Далее следует блок тестирования и графического представления передаточных функций. Поскольку передаточные функции на границах интервала исследования, то есть в начале и конце рабочего хода, не совпадают, для контроля правильности их значений использована процедура TestUniv. Для просмотра графиков ПФ использована процедура Grafik. Контролирующие процедуры расположены в той же последовательности, в какой они определены в программе.
TestUniv (m, dX1, Xa, Xa_1, Xa_2, 'Xa'); Grafik (m+1, X1, Xa_, Xa_1, Xa_2, 'Xa', 'Xa_1', 'Xa_2'); TestUniv (m, dX1, Ya, Ya_1, Ya_2, 'Ya'); Grafik (m+1, X1, Ya_, Ya_1, Ya_2, 'Ya', 'Ya_1', 'Ya_2'); TestUniv (m, dX1, FiABr, FiAB_1, FiAB_2, 'FiAB'); Grafik (m+1, X1, FiABr, FiAB_1, FiAB_2, 'FiAB', 'FiAB_1', 'FiAB_2'); TestUniv (m, dX1, FiCBr, FiCB_1, FiCB_2, 'FiCB'); Grafik (m+1, X1, FiCBr, FiCB_1, FiCB_2, 'FiCB', 'FiCB_1', 'FiCB_2'); TestUniv (m, dX1, FiBDr, FiBD_1, FiBD_2, 'FiBD'); Grafik (m+1, X1, FiBDr, FiBD_1, FiBD_2, 'FiBD', 'FiBD_1','FiBD_2'); TestUniv (m, dX1, Xb, Xb_1, Xb_2, 'Xb'); Grafik (m+1, X1, Xb_, Xb_1, Xb_2, 'Xb', 'Xb_1', 'Xb_2'); TestUniv (m, dX1, Yb, Yb_1, Yb_2, 'Yb'); Grafik (m+1, X1, Yb_, Yb_1, Yb_2, 'Yb', 'Yb_1', 'Yb_2'); TestUniv (m, dX1, Xs2, Xs2_1, Xs2_2, 'Xs2'); Grafik (m+1, X1, Xs2_, Xs2_1, Xs2_2, 'Xs2', 'Xs2_1', 'Xs2_2'); TestUniv (m, dX1, Ys2, Ys2_1, Ys2_2, 'Ys2'); Grafik (m+1, X1, Ys2_, Ys2_1, Ys2_2, 'Ys2', 'Ys2_1', 'Ys2_2'); TestUniv (m, dX1, Xs3, Xs3_1, Xs3_2, 'Xs3'); Grafik (m+1, X1, Xs3_, Xs3_1, Xs3_2, 'Xs3', 'Xs3_1', 'Xs3_2'); TestUniv (m, dX1, Ys3, Ys3_1, Ys3_2, 'Ys3'); Grafik (m+1, X1, Ys3_, Ys3_1, Ys3_2, 'Ys3', 'Ys3_1', 'Ys3_2'); TestUniv (m, dX1, Xs4, Xs4_1, Xs4_2, 'Xs4'); Grafik (m+1, X1, Xs4_, Xs4_1, Xs4_2, 'Xs4', 'Xs4_1', 'Xs4_2'); TestUniv (m, dX1, Ys4, Ys4_1, Ys4_2, 'Ys4'); Grafik (m+1, X1, Ys4_, Ys4_1, Ys4_2, 'Ys4', 'Ys4_1', 'Ys4_2'); TestUniv (m, dX1, Yd, Yd_1, Yd_2, 'Yd'); Grafik (m+1, X1, Yd_, Yd_1, Yd_2, 'Yd', 'Yd_1', 'Yd_2');
Следующим этапом расчёта механизма является его динамический анализ, задачей которого является определение закона изменения скорости и ускорения начального звена - ползуна 1. Из дифференциального уравнения Лагранжа второго рода может быть получено уравнение движения динамической модели механизма для случая линейной обобщённой координаты в форме
где Pпд – приведённая к начальному звену движущая сила, приложенная к поршню гидроцилиндра; Pпс – приведённая к начальному звену сила, учитывающая все внешние силы, кроме движущей; mn – приведённая к начальному звену масса механизма; V1 – линейная скорость начального звена - ползуна 1. Общая формула для определения приведённой силы имеет вид:
Для рассматриваемого механизма
Общая формула для определения приведённой массы имеет вид:
Для рассматриваемого механизма
При расчётах нам понадобится первая производная от приведённой массы по обобщённой координате, которая определяется по общей формуле:
Для рассматриваемого механизма
Для решения динамической задачи необходимо знать характер изменения силы сопротивления при выполнении заданного технологического процесса. Пусть зависимость силы технологического сопротивления от положения ползуна 1 имеет вид, представленный на рис. 23, то есть в начале рабочего хода, когда рабочий орган пресса ещё не вступает в контакт с заготовкой, сила сопротивления равняется нулю, а после начала прессования возрастает по линейному закону до заданной максимальной величины. Будем считать, что силы трения, возникающие при работе механизма, учтены при назначении величины силы сопротивления.
Рисунок 23 - График силы технологического сопротивления Теперь остановимся на определении движущей силы, которую необходимо приложить к ползуну 1, для преодоления всех внешних активных сил, действующих на звенья механизма. Спроектируем механизм таким образом, чтобы линейная скорость ползуна 1 в начале и в конце рабочего хода равнялась нулю. В связи с этим и кинетическая энергия звеньев механизма в начале и конце рабочего хода будут равны нулю. Поэтому движущую силу следует подобрать таким образом, чтобы её работа, которая является величиной положительной, за время рабочего хода равнялась модулю работы остальных внешних сил. Следует заметить, что работа силы сопротивления отрицательна, а вот работа силы тяжести может быть и отрицательной, если ордината центра масс звена увеличивается, и положительной, если центр масс звена опускается. Работа внешних сил, действующих на звенья механизма, может быть представлена в виде
где пределами интегрирования являются начало с координатой 0 и конец рабочего хода ползуна с координатой S1. Полную работу всех внешних сил в конце каждого из 48 интервалов перемещения ползуна удобно определить численным методом в предположении, что на каждом участке приведённая сила изменяется по линейному закону. Тогда
а полная работа за весь рабочий ход составит В свою очередь, работа движущих сил может быть представлена в виде интеграла
В первом приближении величину движущей силы можно принять постоянной и определить из условия равенства модулей работы движущей силы и работы остальных сил, действующих на звенья механизма, то есть
Тогда работа движущей силы в конце каждого из 48 интервалов можно представить в виде
а величина кинетической энергии на границе каждого интервала составит
Зная кинетическую энергию механизма в каждом из 48 положений ползуна, можно определить его линейную скорость
Следует обратить внимание на то, что кинетическая энергия механизма не может быть меньше нуля, что в рабочих условиях соответствует режиму заклинивания механизма. Для преодоления этой возможности следует подобрать рациональный закон изменения силы давления рабочей жидкости на поршень 1. Определив закон изменения скорости ползуна 1, можно определить закон изменения его линейного ускорения, для чего следует проанализировать уравнение движения механизма в дифференциальной форме (???). В результате дифференцирования этого выражения по ОК получим
Учитывая, что
Далее приведен фрагмент программы по определению скорости движения поршня 1, а также его ускорения. { Задание масс звеньев в кг и моментов инерции в кг×мм2 } m1:=30; m2:=20; m3:=100; m4:=80; m5:=200; Is2:=0.5*1000000; Is3:=1*1000000; Is4:=0.5*1000000; g:=9.81; G1y:=-m1*g; { Определение проекций сил тяжести звеньев } G2y:=-m2*g; G3y:=-m3*g; G4y:=-m4*g; G5y:=-m5*g; { Организация цикла расчёта, где m - число шагов начального звена } For i:=1 to m do { Формирование закона изменения силы технологического сопротивления согласно рис. 2 } if i<24 Then Pc[i]:=0 Else Pc[i]:=50000*(i-24)/24; { Вывод на экран графика силы сопротивления } Grafik (m+1, X1, Pc, zz, zz, 'Pc', '', ''); { Определение массива значений приведённой силы } For i:=1 to m+1 Do Pnc[i]:=G1y*Ya_1[i]+G2y*Ys2_1[i]+G3y*Ys3_1[i]+G4y*Ys4_1[i]+ (G5y+Pc[i])*Yd_1[i]; { Определение работы внешних сил в конце каждого шага ползуна } Sum:=0; Ac[1]:=0; Ad[1]:=0; For i:=1 to m do Ac[i+1]:=Ac[i]+(Pnc[i]+Pnc[i+1])/2*(dX1); Acopr:=Ac[49]; { Работа внешних сил за рабочий ход ползуна } Adw:=-Acopr; { Работа движущей силы за рабочий ход ползуна } Pndcp:=Adw/m/dX1; { Среднее значение движущей силы } { Задание закона изменения движущей силы, обеспечивающего отсутствие заклинивания } For i:=1 to m+1 do Begin if i<=24 Then Pnd[i]:=(Pndcp+200.0) Else if i=25 Then Pnd[i]:=Pndcp Else if i>25 Then Pnd[i]:=(Pndcp-200.0); End; { For } { Вывод графиков приведённой движущей силы Pnd и остальных внешних сил Pnc, которые представлены на рис. 24 } Grafik (m+1, X1, Pnc, Pnd, zz, 'Pnc', 'Pnd', '');
Рисунок 24 – Графики приведённых сил, действующих на звенья пресса { Примерным визуальным критерием правильности этих графиков является равенство площадей под этими линиями, представляющих работу соответствующих сил за период рабочего хода }
{ Определение работы движущей силы в конце каждого шага ползуна } Ad[1]:=0; For i:=1 to m do Begin Ad[i+1]:=Ad[i]+(Pnd[i]+Pnd[i+1])/2*(dX1); Ad_[i+1]:=-Ad[i+1]; End; { For } { Вывод графиков работы движущей и остальных сил, действующих на звенья механизма } Grafik (m+1, X1, Ac, Ad, Ad_, 'Ac', 'Ad', 'Ad_'); { Определение закона изменения кинетической энергии механизма } T[1]:=0; For i:=1 to m+1 do T[i+1]:=T[i]+(Ad[i+1]+Ac[i+1])-(Ad[i]+Ac[i]); { Вывод графика изменения кинетической энергии механизма. При просмотре этого графика следует убедиться, что кинетическая энергия ни в одном из положений не является отрицательной. В противном случае следует перезадать закон изменения движущей силы } Grafik (m+1, X1, T, zz, zz, 'T', '', ''); { Организация цикла по расчёту приведённой к начальному звену массы механизма и её производной по ОК. } For i:=1 to m+1 do Begin mp[i]:=m1 + m2*(sqr(Xs2_1[i]) + sqr(Ys2_1[i])) + Is2*sqr(FiAB_1[i]) + m3*(sqr(Xs3_1[i]) + sqr(Ys3_1[i])) + Is3*sqr(FiCB_1[i]) + m4*(sqr(Xs4_1[i]) + sqr(Ys4_1[i])) + Is4*sqr(FiBD_1[i]) + m5*sqr(Yd_1[i]); mp_1[i]:=2*(m2*(Xs2_1[i]*Xs2_2[i] + Ys2_1[i]*Ys2_2[i]) + m3*(Xs3_1[i]*Xs3_2[i] + Ys3_1[i]*Ys3_2[i]) + m4*(Xs4_1[i]*Xs4_2[i] + Ys4_1[i]*Ys4_2[i]) + m5*Yd_1[i]*Yd_2[i]) + 2*(Is2*Fiab_1[i]*Fiab_2[i] + Is3*Ficb_1[i]*Ficb_2[i] + Is4*Fibd_1[i]*Fibd_2[i]); End; { For } { Тестирование и вывод графиков этих параметров } TestUniv (m, dX1, mp, mp_1, zz, 'mp'); Grafik (m+1, X1, mp, mp_1, zz, 'mp', 'mp_1', ''); { Определение массивов скорости и ускорения ползуна 1, а также величины For i:=1 to m+1 do Begin V1[i]:=sqrt(T[i]*2/mp[i]); w1[i]:=1/mp[i]*(Pnd[i]+Pnc[i]-mp_1[i]*sqr(V1[i])/2); V1[1]:=0.01;V1[49]:=0.01;V1_1[i]:=W1[i]/V1[i]; End; { For } { Тестирование скорости ползуна и вывод графиков скорости и ускорения } TestUniv (m, dX1, V1, V1_1, zz, 'V1'); Grafik (m+1, X1, V1, W1, zz, 'V1', 'W1', ''); Следующим этапом расчёта механизма является его кинематический анализ, включающий определение линейных и угловых скоростей и ускорений элементов механизма. Проекции линейной скорости произвольной точки звена определяются по формулам:
а угловая скорость по формуле
Проекции линейного ускорения произвольной точки звена определяются по формулам:
Угловое ускорение звена:
Ниже приведен фрагмент программы для определения проекций ускорений центров масс звеньев, а также угловых ускорений звеньев.
For i:=1 to m+1 do Begin aax:=Xa_2[i]*sqr(V1[i])+Xa_1[i]*W1[i]; aay:=Ya_2[i]*sqr(V1[i])+Ya_1[i]*W1[i]; as2x:=Xs2_2[i]*sqr(V1[i])+Xs2_1[i]*W1[i]; as2y:=Ys2_2[i]*sqr(V1[i])+Ys2_1[i]*W1[i]; as3x:=Xs3_2[i]*sqr(V1[i])+Xs3_1[i]*W1[i]; as3y:=Ys3_2[i]*sqr(V1[i])+Ys3_1[i]*W1[i]; as4x:=Xs4_2[i]*sqr(V1[i])+Xs4_1[i]*W1[i]; as4y:=Ys4_2[i]*sqr(V1[i])+Ys4_1[i]*W1[i]; ady:=Yd_2[i]*sqr(V1[i])+Yd_1[i]*W1[i]; e2:=Fiab_2[i]*sqr(V1[i])+Fiab_1[i]*W1[i]; e3:=Ficb_2[i]*sqr(V1[i])+Ficb_1[i]*W1[i]; e4:=Fibd_2[i]*sqr(V1[i])+Fibd_1[i]*W1[i]; End; { For } Следующим этапом является силовой расчёт механизма, целью которого является определение реакций в кинематических парах и, следовательно, нагрузки на звенья. Посколку в основу силового расчёта положен принцип Даламбера, необходимо определить проекции главного вектора сил инерции каждого звена и главный момент сил инерции. Проекции главного вектора сил инеции i -го звена определяются по формулам:
Главный момент сил инерции звена
Ниже приведен фрагмент программы для определения сил инерции.
For i:=1 to m+1 do Begin Fi1x[i]:=-m1*aax; Fi1y[i]:=-m1*aay; Fi2x[i]:=-m2*as2x; Fi2y[i]:=-m2*as2y; Fi3x[i]:=-m3*as3x; Fi3y[i]:=-m3*as3y; Fi4x[i]:=-m4*as4x; Fi4y[i]:=-m4*as4y; Fi5y[i]:=-m5*ady; Mf2[i]:=-Is2*e2; Mf3[i]:=-Is3*e3; Mf4[i]:=-Is4*e4; End; { For }
Для проверки правильности выполненных расчётов следует воспользоваться принципом Лагранжа, который в данном случае может быть сформулирован следующим образом: алгебраическая сумма приведённых к начальному звену всех внешних сил и сил инерции равняется нулю. Ниже приводится фрагмент программы для определения этой суммы для каждого из 48 положений начального звена. В программе этой сумме, которая является машинным нулём, присваивается имя Pogr. Этот массив выводится на экран с помощью процедуры Grafik, и расчёт считается правильным, если ординаты этого графика действительно являются машинными нулями, то есть очень малыми величинами. В противном случае следует искать ошибку, используя метод обнуления масс.
For i:=2 to m+1 do Pogr[i]:=Pnd[i]+Fi1x[i]*Xa_1[i]+(Fi1y[i]+G1y)*Ya_1[i]+ Fi2x[i]*Xs2_1[i]+(Fi2y[i]+G2y)*Ys2_1[i]+ Fi3x[i]*Xs3_1[i]+(Fi3y[i]+G3y)*Ys3_1[i]+ Fi4x[i]*Xs4_1[i]+(Fi4y[i]+G4y)*Ys4_1[i]+ (Fi5y[i]+G5y+Pc[i])*Yd_1[i]+Mf2[i]*Fiab_1[i]+ Mf3[i]*Ficb_1[i]+Mf4[i]*Fibd_1[i]; Grafik (m+1, X1, Pogr, zz, zz, 'Pogr', '', '');
Силовой расчёт механизма выполняется по группам Ассура, так как они являются статически определимыми системами. Причём сначала рассчитывается группа, которая соединена с другой частью механизма двумя кинематическими парами. Такой является группа Ассура второго вида, включающая шатун 4 и ползун 5. На рисунке приведена схема нагружения звеньев группы и реакции в КП для одного из положений механизма.
Рисунок 25 - Схема нагружения группы второго вида
Для определения реакций следует воспользоваться процедурой Sila2, описание которой имеет следующий вид:
Sila2 (G2у, G3y: Real; var Xа, Yа, Xb, Yb, Fing, Mc2, Xk2, Yk2, P2x, P2y, Mf2, Xs2, Ys2, F2x, F2y, Mc3, Xk3, Yk3, P3x, P3y, Mf3, Xs3, Ys3, F3x, F3y, Rax, Ray, R32x, R32y, Rnx, Rny, Mn: Massiv);
При обращении к этой процедуре следует иметь в виду, что звенья с номерами 2 и 3 в рассчитываемом механизме имеют номера 4 и 5, а имена кинематических пар В и D вместо А и В. Фрагмент программы силового расчёта приведен ниже. Сначала формируется массив одинаковых значений угла направляющей ползуна 5, а затем момент сил инерции шатуна 4 переводится из Нмм в Нм. При обращении к процедуре Sila2 имя zz представляет нулевой массив.
For i:=1 to m+1 do Begin Fin5g[i]:=90; mf4_[i]:=Мf4[i]/1000 End; { For }
|
||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 220; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.194.29 (0.007 с.) |

 , (69)
, (69) . (70)
. (70)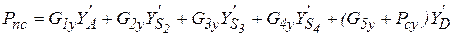 . (71)
. (71) . (72)
. (72) (73)
(73) . (74)
. (74)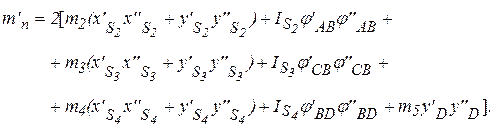 (75)
(75)
 , (76)
, (76) , (77)
, (77) .
. . (78)
. (78)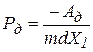 . (79)
. (79) , (80)
, (80)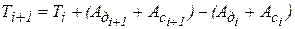 . (81)
. (81)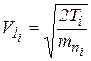 . (82)
. (82)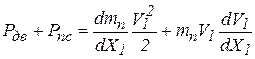 . (83)
. (83)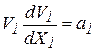 , получим
, получим . (84)
. (84)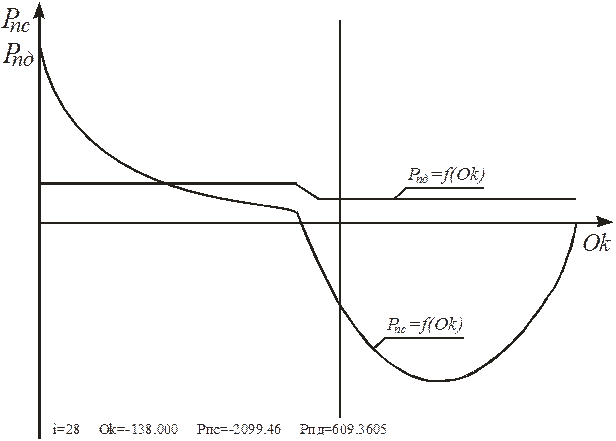
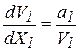 }
}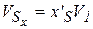 , (85)
, (85) , (86)
, (86) . (87)
. (87) , (88)
, (88)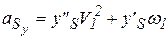 . (89)
. (89) . (90)
. (90)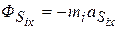 , (91)
, (91) . (92)
. (92) . (93)
. (93)