
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оценка параметров уравнения множественной регрессии
При оценке параметров уравнения регрессии применяется МНК. При этом делаются определенные предпосылки относительно случайной составляющей
Система нормальных уравнений:
МНОЖЕСТВЕННАЯ КОРРЕЛЯЦИЯ Практическая значимость уравнения регрессии оценивается с помощью индекса множественной корреляции и его квадрата – коэффициента множественной детерминации. Независимо от формы связи показатель множественной корреляции может быть найден как индекс множественной корреляции. Обозначим
где
где Иначе, формула примет вид:
Отсюда следует 0≤R≤1. Этот показатель характеризует тесноту связи рассматриваемого набора факторов с используемым признаком, т.е. оценивает тесноту связи совместного влияния факторов на результат. При линейной зависимости признаков формула индекса корреляции имеет вид:
где
Возможен иной подход к определению параметров, когда на основе матрицы парных коэффициентов корреляции строится уравнение регрессии в стандартизованном масштабе
а среднее квадратичное отклонение Применяя МНК к уравнению множественной регрессии в стандартизованном масштабе, получим систему нормальных уравнений вида
Решая систему, найдем параметры. Стандартизованные параметры
Для МНК имеем формулы:
Таким образом, в системе вычисляется коэффициент корреляции по формуле:
так как Стандартизованные коэффициенты регрессии где βj – показывает, на сколько величин Э
КОЭФФИЦИЕНТ ДЕТЕРМИНАЦИИ
Отметим ещё одну формулу для коэффициента детерминации:
Вместе с тем использование только одного коэффициента детерминации для выбора наилучшего уравнения регрессии может оказаться недостаточным. На практике встречаются случаи, когда плохо определяется модель регрессии и может дать сравнительно высокий коэффициент
из этой формулы следует: чем больше число объясняющих переменных p,тем меньше Очевидно, скорректированный коэффициент может уменьшаться при введении в модель новых объясняющих переменных, не оказывающих существенного влияния на зависимую переменную. Если известен
ЧАСТНЫЕ УРАВНЕНИЯ РЕГРЕССИИ На основе линейного уравнения множественной регрессии
могут быть найдены частные уравнения регрессии:
…
то есть уравнения регрессии, которые связывают результативный признак y с соответствующими факторами x при закреплении других, учитываемых во множественной регрессии на среднем уровне:
…
При подстановке в эти уравнения средних значений соответствующих факторов, они принимают вид парных уравнений линейной регрессии:
…
…
Частные уравнения характеризуют изолированное влияние фактора на результат, ибо другие факторы закреплены. Это позволяет на основе частных уравнений определять частные коэффициенты эластичности.
ЧАСТНЫЕ ИНДЕКСЫ КОРРЕЛЯЦИИ В случае, когда имеется одна независимая и одна зависимая переменные, естественной мерой зависимости (в рамках линейного подхода) является (выборочный) коэффициент корреляции между ними. Использование множественной регрессии позволяет обобщить это понятие на случай, когда имеется несколько независимых переменных. Корректировка здесь необходима по следующим очевидным соображениям. Высокое значение коэффициента корреляции между исследуемой зависимой и какой-либо независимой переменной может, как и раньше, означать высокую степень зависимости, но может быть обусловлено и другой причиной. А именно, есть третья переменная, которая оказывает сильное влияние на две первые, что и служит, в конечном счете, причиной их высокой коррелированности. Поэтому возникает естественная задача найти “чистую” корреляцию между двумя переменными, исключив (линейное) влияние других факторов. Рассуждения здесь могут быть такими. Обозначим остаточную дисперсию
Включим в уравнение регрессии ещё один фактор
Чем меньше доля этого сокращения в остаточной вариации до введения дополнительного фактора, то есть в Следовательно, чистое влияние фактора
аналогично, чистое влияние на результат фактора
Если выразить остаточную дисперсию через показатель детерминации, аналогично,
Преобразуем полученную формулу:
Из приведённых формул частных коэффициентов корреляции, видна связь этих показателей с совокупным коэффициентом корреляции. Зная частные коэффициенты корреляции последовательного первого, второго, и так далее, порядка, совокупный коэффициент корреляции получается.
При полной зависимости результативного признака от исследуемых факторов корреляции, совокупного их влияния, коэффициент корреляции равен единице. Из единицы вычитается доля остаточной вариации результативного признака
|
||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 315; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.40.177 (0.033 с.) |

 .
.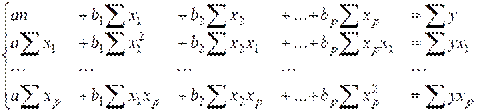
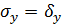 , тогда
, тогда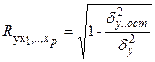 , -при любой форме связи
, -при любой форме связи – общая дисперсия результативного признака,
– общая дисперсия результативного признака, – остаточная дисперсия для уравнения
– остаточная дисперсия для уравнения 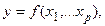
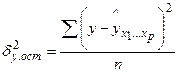 , так как
, так как 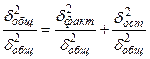 .
.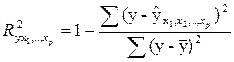 .
.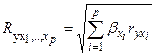
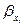 – стандартизованные коэффициенты регрессии,
– стандартизованные коэффициенты регрессии,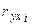 – парные коэффициенты корреляции результата с каждым фактором.
– парные коэффициенты корреляции результата с каждым фактором. , где
, где 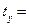
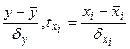
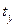 и
и  - стандартизованные переменные, для которых среднее значение равно нулю
- стандартизованные переменные, для которых среднее значение равно нулю  , так как
, так как 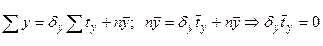
 так как
так как 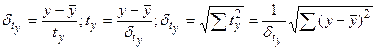 .
.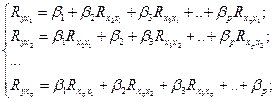
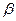 – показывают, на сколько сигм изменится в среднем результат, если увеличить соответствующий фактор
– показывают, на сколько сигм изменится в среднем результат, если увеличить соответствующий фактор 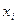 на одну сигму при неизменном среднем уровне других факторов. В силу того, что все переменные заданы как централизованные и нормированные, то
на одну сигму при неизменном среднем уровне других факторов. В силу того, что все переменные заданы как централизованные и нормированные, то 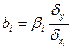
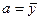
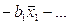


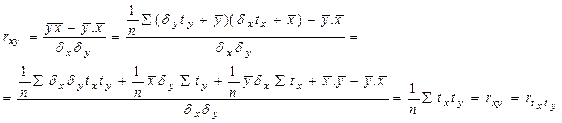
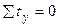 ,
, 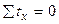 , и он равен коэффициенту корреляции в стандартизованных переменных.
, и он равен коэффициенту корреляции в стандартизованных переменных. связаны с коэффициентом регрессии
связаны с коэффициентом регрессии  и коэффициентом эластичности Э
и коэффициентом эластичности Э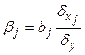 ,
, 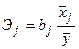
 изменится в среднем y при увеличении только j -ой объясняющей переменной на
изменится в среднем y при увеличении только j -ой объясняющей переменной на  .
.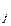 – коэффициент эластичности показывает, на сколько процентов от средней величины изменится в среднем y при увеличении только
– коэффициент эластичности показывает, на сколько процентов от средней величины изменится в среднем y при увеличении только  на один процент.
на один процент.
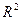 . Недостатком коэффициента
. Недостатком коэффициента 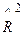 , определяемый по формуле:
, определяемый по формуле: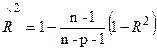
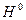 о равенстве нулю параметров регрессионной модели
о равенстве нулю параметров регрессионной модели 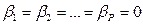 отвергается, или уравнение регрессии значимо, если
отвергается, или уравнение регрессии значимо, если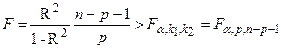 (1) - табличное значение
(1) - табличное значение  - критерия Фишера, где α – уровень значимости, n – число наблюдений, p – число факторов.
- критерия Фишера, где α – уровень значимости, n – число наблюдений, p – число факторов.
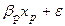
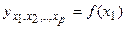
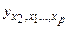
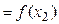
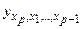
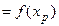

 +
+  +…+
+…+ 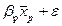
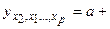
 +
+ 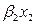 +…+
+…+ 

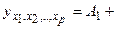



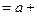
 +…+
+…+  ;
;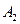

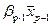
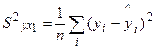
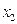 , его включение приведет к уменьшению остаточной дисперсии. Чем больше число факторов включения в модель, тем меньше величина остаточной дисперсии. Сокращение остаточной дисперсии за счет дополнительного введения фактора
, его включение приведет к уменьшению остаточной дисперсии. Чем больше число факторов включения в модель, тем меньше величина остаточной дисперсии. Сокращение остаточной дисперсии за счет дополнительного введения фактора 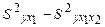
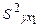 , тем теснее связь между
, тем теснее связь между 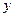 и
и 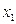 . Корень квадратный из этой величины и есть индекс частной корреляции, показывающий в чистом виде тесноту связи
. Корень квадратный из этой величины и есть индекс частной корреляции, показывающий в чистом виде тесноту связи  ,
, .
.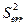 =
= 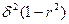 то формула коэффициента частной корреляции примет вид:
то формула коэффициента частной корреляции примет вид: 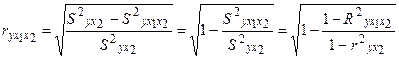
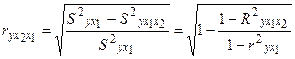 .
.
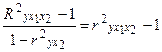 , отсюда
, отсюда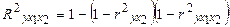 , обобщая эту формулу на p независимых переменных, получим
, обобщая эту формулу на p независимых переменных, получим
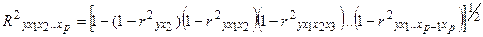
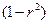 , обусловленная последовательно включёнными в анализ факторами. В результате подкоренное выражение характеризует совокупное действие всех исследуемых факторов.
, обусловленная последовательно включёнными в анализ факторами. В результате подкоренное выражение характеризует совокупное действие всех исследуемых факторов.


