
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Этапы построения эконометрической моделиСтр 1 из 9Следующая ⇒
ЭТАПЫ ПОСТРОЕНИЯ ЭКОНОМЕТРИЧЕСКОЙ МОДЕЛИ
1. Качественный анализ сущности рассматриваемого явления и выдвижение гипотезы. 2. Формирование набора факторов, участвующих в модели и их анализ. 3. Сбор необходимой статистической информации. 4. Проведение спецификации модели, т.е. выбор общего вида модели, в том числе состава и формы входящих в неё связей между переменными. 5. Проведение оценки параметров уравнения. 6. Проверка адекватности модели, оценка точности модельных данных. 7. Интерпретация результатов моделирования. 8. Прогнозирование неизвестных значений зависимой переменной.
2. ПАРНАЯ РЕГРЕССИЯ
Парная регрессия – уравнение связи двух переменных у и x:
Различают линейные и нелинейные регрессии. Линейная:
Нелинейные регрессии делят на два класса: регрессии, нелинейные относительно включенных объясняющих переменных, но линейных по оцениваемым параметрам, и, регрессии, нелинейные по оцениваемым параметрам.
Нелинейные по объясняющим переменным, но линейная по оцениваемым параметрам:
Регрессии, нелинейные по оцениваемым параметрам: Степенная: Показательная: Экспоненциальная: Логарифмическая: Полулогарифмическая: Обратная:
Нашей задачей является подобрать функцию
2.1. СПЕЦИФИКАЦИЯ МОДЕЛИ ГРАФИЧЕСКИМ МЕТОДОМ
Этот метод применяют в случае парной зависимости для наглядного изображения формы связи между изучаемыми экономическими показателями. Для этого в прямоугольной системе координат строят график, по оси ординат откладывают значения результативного признака Y, а по оси абсцисс - значения факторного признака X. Совокупность точек результативного и факторного признаков называется полем корреляции. На основании поля корреляции можно выдвинуть гипотезу о типе связи между всеми возможными значениями X и Y.

Рисунок 1. Графики различных функций. ОЦЕНКА ПАРАМЕТРОВ МОДЕЛИ
Построение уравнения регрессии сводится к оценке её параметров. Согласно МНК (метод наименьших квадратов) поиск наилучшей аппроксимации набора наблюдений сводится к минимизации функционала:
Для линейной функции:
Необходимые условия экстремума:
Введем обозначения:
В новых обозначениях система определения
2.3. ОЦЕНКА КАЧЕСТВА ЭКОНОМЕТРИЧЕСКОЙ МОДЕЛИ
Проверить значимость уравнения регрессии - значит установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной. На первый взгляд, подходящим измерителем тесноты связи Очевидно, что для использования
Таблица 1. Показатели качества модели
КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ
Статистика применяет систему, которая использует в качестве единицы измерения переменной её среднее квадратическое отклонение Подставив правую часть равенства (7) в уравнение
т.о. В этой системе величина Для практических расчетов наиболее удобна формула:
Свойства коэффициента корреляции: 1) 2) при
3) при Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока: 0.1 < rxy < 0.3: слабая; 0.3 < rxy < 0.5: умеренная; 0.5 < rxy < 0.7: заметная; 0.7 < rxy < 0.9: высокая; 0.9 < rxy < 1: весьма высокая; Близость к нулю не означает отсутствия связи между признаками, она может оказаться достаточно тесной, но иметь нелинейную зависимость. КОЭФФИЦИЕНТ ДЕТЕРМИНАЦИИ
Проверка значимости уравнения регрессии производится на основе дисперсионного анализа. Обозначим через
Преобразуем формулу дисперсии с учетом вышеуказанной суммы:
Далее
Так как имеет место равенство и из МНК следуют два соотношения то
Введем обозначения: TSS (total sum of sguares) – вся дисперсия: сумма квадратов отклонений от среднего. RSS (regression sum of sguares) – объясненная часть всей дисперсии (обусловленная регрессией). ESS (error sum of sguares) – остаточная сумма, дисперсия остаточная.
Коэффициентом детерминации, или долей объясненной дисперсии называется:
Для линейной регрессии: Тогда, Отсюда, можно выразить индекс корреляции R для нелинейной регрессии
Свойства коэффициента детерминации: 1) в силу определения 2) если 3) если
F-КРИТЕРИЙ ФИШЕРА
Оценка качества уравнения регрессии состоит в проверке гипотезы
где m – число степеней свободы, для парной регрессии m=1
Если Если ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача 1. При исследовании 8 магазинов получены следующие данные (табл.3). 1. Построить регрессионную модель зависимости объема товарооборота от числа работников. 2. Проверить значимость модели и коэффициентов модели. 3. Рассчитать коэффициент эластичности и дать ему экономическую интерпретацию. 4. Построить 95% доверительный интервал для оценки объема товарооборота отдельного магазина со 100 работниками. Таблица 3. Исходные данные к Задаче 1.
Решение: a. Проведем спецификацию модели графическим методом. Поскольку необходимо найти зависимость объема товарооборота от числа работников, то в качестве Y – принимаем Объем товарооборота, X - Число работников.
Рисунок 2. Спецификация модели На основании поля корреляции можно выдвинуть гипотезу о том, что связь между всеми возможными значениями X и Y носит линейный характер. Для оценки параметров a и b - используют МНК (метод наименьших квадратов). b. Параметры уравнения регрессии. Выборочные средние:
Таблица 4. Расчет параметров модели
Используя формулы (6) и (7), получаем коэффициенты регрессии: b = 0.0192, a = -0.97. (b>0, следовательно связь прямая) Уравнение регрессии: y = 0.0192 x - 0.97, Величина коэффициента b говорит о том, что с ростом числа работников на 1 человека, объем товарооборота магазина будет увеличиваться на 0,0192 млн. руб. c. Теснота связи.
Среднеквадратическое отклонение:
Рассчитываем показатель тесноты связи. Таким показателем является линейный коэффициент корреляции, который рассчитывается по формуле:
В нашем примере связь между признаком Y и фактором X (по шкале Чеддока) весьма высокая. Кроме того, коэффициент линейной парной корреляции может быть определен через коэффициент регрессии b:
Незначительные отклонения в расчетных величинах возможны из-за округления величин. d. Коэффициент детерминации. Подставив в уравнение регрессии соответствующие значения х, можно определить выровненные (модельные) значения результативного показателя y(x) для каждого наблюдения.
т.е. в 97.12 % случаев изменения х приводят к изменению y. Другими словами - точность подбора уравнения регрессии - высокая. Остальные 2.88 % изменения Y объясняются факторами, не учтенными в модели. Таблица 5. Расчет промежуточных величин для оценки качества модели
5. Критерий Фишера.
Табличное значение критерия со степенями свободы k1=1 и k2=6 (8-1-1), Fтабл = 5.99 Поскольку фактическое значение Fфакт > Fтабл, то коэффициент детерминации статистически значим (найденная оценка уравнения регрессии статистически надежна). 6. Ошибка аппроксимации. Оценим качество уравнения регрессии с помощью ошибки абсолютной аппроксимации. Средняя ошибка аппроксимации - среднее отклонение расчетных значений от фактических:
Ошибка аппроксимации в пределах 5%-7% свидетельствует о хорошем подборе уравнения регрессии к исходным данным. Поскольку ошибка меньше 7%, то данное уравнение можно использовать в качестве регрессии. 7. Проверка статистической значимости параметров. Несмещенной оценкой дисперсии возмущений является величина:
Стандартное отклонение случайной величины a:
Стандартное отклонение случайной величины b:
Поскольку 14.12 > 2.447, то статистическая значимость коэффициента регрессии b подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).
Поскольку 6.2 > 2.447, то статистическая значимость коэффициента регрессии a подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента). 8. Доверительный интервал для коэффициентов уравнения регрессии. Определим доверительные интервалы коэффициентов регрессии, которые с надежностью 95% будут следующими: (b – tтабл mb; b + tтабл mb) = (0.0192 - 2.447 • 0.00136; 0.0192 + 2.447 • 0.00136) = = (0.0158;0.0225) С вероятностью 95% можно утверждать, что значение данного параметра будет лежать в найденном интервале. (a – tтабл ma; a + tтабл ma) = (-0.9739 - 2.447 • 0.156; -0.9739 + 2.447 • 0.156) = = (-1.356;-0.5922) С вероятностью 95% можно утверждать, что значение данного параметра будет лежать в найденном интервале. 9. Коэффициент эластичности. Коэффициенты регрессии (в примере b) нежелательно использовать для непосредственной оценки влияния факторов на результативный признак в том случае, если существует различие единиц измерения результативного показателя у и факторного признака х. Для этих целей вычисляются коэффициенты эластичности и бета - коэффициенты. Средний коэффициент эластичности E показывает, на сколько процентов в среднем по совокупности изменится результат у от своей средней величины при изменении фактора x на 1% от своего среднего значения. Коэффициент эластичности находится по формуле:
В нашем примере коэффициент эластичности больше 1. Следовательно, при изменении Х на 1%, Y изменится более чем на 1%. Другими словами - Х существенно влияет на Y.
10. Интервальный прогноз. Точечный прогноз показателя
Далее вычисляется средняя стандартная ошибка прогноза
Строится доверительный интервал прогноза:
Задача 2. Имеются данные о количестве выпускаемой продукции в тыс. штук (x) и ее себестоимостью в у.е. (y).
Таблица 6. Исходные данные к Задаче 2.
1. Для характеристики зависимости у от х рассчитать параметры следующих функций: а) линейной; б) степенной; в) показательной; г) равносторонней гиперболы. 2. Оценить каждую модель через среднюю ошибку аппроксимации 3. Выбрать лучшую модель для прогноза.
Проведем спецификацию модели графическим методом.
Рисунок 3. Поле корреляции к Задаче 2.
Построим линейную и нелинейные регрессии и оценим их качество.
A. Линейная модель. Для расчета параметров a и b линейной регрессии y=a=b*x рассчитываем
Таблица 7. Расчет параметров линейной модели.
Уравнение регрессии: C увеличением количества выпускаемой продукции на 1 тыс., ее себестоимость снижается в среднем на 0,4671 у.е. Рассчитаем линейный коэффициент парной корреляции. Среднеквадратическое отклонение:
Связь обратная и весьма высокая. Определим коэффициент детерминации:
Вариация результата на 86% объясняется вариацией фактора x. Таблица 7. Расчет промежуточных величин для оценки качества линейной модели
Найдем величину средней ошибки аппроксимации
Рассчитываем F - критерий:
Fтабл = 4,7472. Так как Fфакт > Fтабл, уравнение регрессии значимо. B. Степенная модель. Построению степенной модели
Где Y=lg y, X= lg x, C= lg a. Для расчетов используем данные Таблицы 8. Таблица 8. Расчет параметров степенной модели.
Сумма Среднее Рассчитаем С и b:
Получим линейное уравнение: Выполнив его потенцирование, получим:
Подставляя в данное уравнение фактические значения x, получаем теоретические значения результата
Связь весьма высокая. Определим индекс детерминации:
Вариация результата на 99% объясняется вариацией фактора x.
Расчетные значения в среднем откланяются от фактических на 3,6 %. Таблица 9. Расчет величин для оценки качества степенной модели.
Рассчитываем F - критерий:
Fтабл = 4,7472. Так как Fфакт > Fтабл, уравнение регрессии значимо, статистически надежно. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ.
Задание 1. По семи территориям Уральского района известны значения двух признаков. Таблица 15. Исходные данные к Заданию 1.
Требуется: 1. Для характеристики зависимости у от х рассчитать параметры следующих функций: а) линейной; б) степенной; в) равносторонней гиперболы; *г) показательной. 2. Оценить каждую модель через среднюю ошибку аппроксимации Результаты занести в таблицу 16.
Таблица 16. Результат регрессионного анализа Задания 1.
* - задание повышенной сложности.
Задание 2.
По группе предприятий, производящих однородную продукцию, известно, как зависит себестоимость единицы продукции у от факторов, приведенных в табл. 17. Таблица 17. Исходные данные к Заданию 2.
Требуется: 1. Определить с помощью коэффициентов эластичности силу влияния каждого фактора на результат. 2. Ранжировать факторы по силе влияния. ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
Сформулировать гипотезу о взаимосвязи двух экономических показателях и провести эконометрическое исследование на основе реальных статистических данных, полученных из официальных источников статистической информации (Государственного комитета статистики РФ, международных финансовых организаций и др.).
*- По результатам проведенного эконометрического исследования подготовить научную статью для публикации в периодических научных изданиях.
Парная регрессия может дать хороший результат при моделировании, если влиянием других факторов, воздействующих на объект исследования, можно пренебречь. Если это невозможно, то следует попытаться выявить влияние других факторов, вводя их в модель, т.е. построить модель множественной регрессии
| Поделиться:
| |

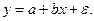






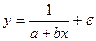
 , наилучшим способом описывающую зависимость y от x.
, наилучшим способом описывающую зависимость y от x.


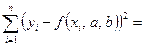
 . (1)
. (1) (2)
(2) (3);
(3);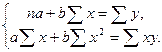 (4)
(4) ,
,  ,
, 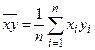 ,
,  .
. и
и  принимает вид:
принимает вид: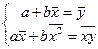 (5)
(5)
 , (6)
, (6) , (7)
, (7) - выборочной дисперсии переменной x;
- выборочной дисперсии переменной x; - выборочной дисперсии переменной y;
- выборочной дисперсии переменной y; - выборочной ковариации.
- выборочной ковариации.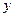 от
от  является коэффициент регрессии
является коэффициент регрессии  ,
где
,
где  ,
, 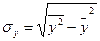





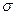 .
. , получим:
, получим:
 .
. показывает, на сколько величин
показывает, на сколько величин  изменится в среднем
изменится в среднем  . Величина
. Величина  (8)
(8)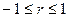 , т.к.
, т.к.  ;
; , корреляционная связь представляет линейную функциональную зависимость. При этом все наблюдаемые значения располагаются на прямой.
, корреляционная связь представляет линейную функциональную зависимость. При этом все наблюдаемые значения располагаются на прямой. линейная связь отсутствует.
линейная связь отсутствует. - модельные, теоретически вычисляемые по формуле значения, тогда
- модельные, теоретически вычисляемые по формуле значения, тогда (9)
(9) (10)
(10) (11)
(11) ,
, , (12)
, (12)
 (13)
(13)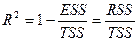 .
. или
или  .
. . Получившаяся формула есть дисперсия объясненная, факторная, тогда
. Получившаяся формула есть дисперсия объясненная, факторная, тогда  .
. . (14)
. (14) .;
.; , то регрессия ничего не дает, т.е.
, то регрессия ничего не дает, т.е. 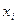 не улучшает качество предсказания
не улучшает качество предсказания  , по сравнению с
, по сравнению с  .
. , то
, то  лежат на линии регрессии и между
лежат на линии регрессии и между  .
. о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого производится сравнение фактического
о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого производится сравнение фактического 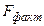 и
и  значений F-критерия Фишера-Снедекора.
значений F-критерия Фишера-Снедекора.  . (15)
. (15) . Уровень значимости
. Уровень значимости  .
.
 ,
, 



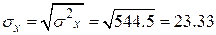 ,
, 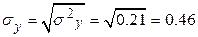
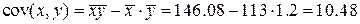



 .
.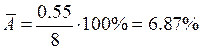
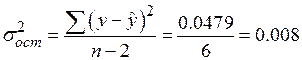 - необъясненная дисперсия (мера разброса зависимой переменной вокруг линии регрессии).
- необъясненная дисперсия (мера разброса зависимой переменной вокруг линии регрессии). - стандартная ошибка оценки (стандартная ошибка регрессии).
- стандартная ошибка оценки (стандартная ошибка регрессии).








 определяется путем подстановки в уравнение регрессии
определяется путем подстановки в уравнение регрессии  0.0192 x - 0.97 соответствующего прогнозного значения
0.0192 x - 0.97 соответствующего прогнозного значения  =100.
=100.
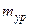 :
:



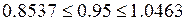
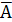 и F-критерий Фишера.
и F-критерий Фишера.
 ,
,  ,
,  ,
,  ,
,  .
.

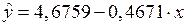 .
. ;
;  .
. ;
;  .
. .
. .
.

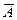 :
: .
.
 предшествует процедура линеаризации переменных. В примере линеаризация производится путем логарифмирования обеих частей уравнения:
предшествует процедура линеаризации переменных. В примере линеаризация производится путем логарифмирования обеих частей уравнения:



 .
.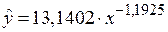 .
.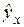 . По ним рассчитываем показатели: тесноты связи - индекс корреляции R и среднюю оценку аппроксимации
. По ним рассчитываем показатели: тесноты связи - индекс корреляции R и среднюю оценку аппроксимации  .
.
 .
.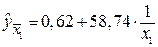
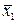 =2.64
=2.64
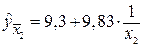
 =1,38
=1,38
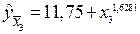
 =1,503
=1,503
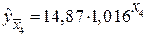
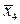 =26,3
=26,3



