
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интерпретация результатов моделирования
В линейной эконометрической модели Коэффициент Связь между у и х определяет знак коэффициента регрессии b (если > 0 – прямая связь, иначе - обратная). Значительный интерес для экономических исследований представляют коэффициенты эластичности, найденные по уравнениям регрессии. Т.к. коэффициент Э не всегда const, то используем среднее значение -
Таблица 2. Нахождение коэффициентов эластичности
Средний коэффициент эластичности
В таблице представлены формулы для нахождения коэффициента эластичности для наиболее часто встречающихся функций.
ПРОГНОЗИРОВАНИЕ НЕИЗВЕСТНЫХ ЗНАЧЕНИЙ ЗАВИСИМОГО ПРИЗНАКА Y Если модель регрессии значима в целом, предположение о незначимости отклоняется по всем параметрам функции регрессии, не нарушены предпосылки МНК, то модель может быть использована для анализа и прогнозов количественного показателя экономики. Условно «лучшей» моделью для анализа и прогнозов исследуемого показателя можно считать ту, для которой: v показатель детерминации – выше, v стандартная ошибка – меньше, v доверительный интервал прогноза уже. Различают точечный и доверительный (интервальный) прогнозы моделируемого показателя (y). Точечный прогноз показателя Интервальный прогноз показателя с заданной доверительной вероятностью (P=a-1) имеет вид:
Вычисляется средняя стандартная ошибка прогноза
и строится доверительный интервал прогноза
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача 1. При исследовании 8 магазинов получены следующие данные (табл.3). 1. Построить регрессионную модель зависимости объема товарооборота от числа работников.
2. Проверить значимость модели и коэффициентов модели. 3. Рассчитать коэффициент эластичности и дать ему экономическую интерпретацию. 4. Построить 95% доверительный интервал для оценки объема товарооборота отдельного магазина со 100 работниками. Таблица 3. Исходные данные к Задаче 1.
Решение: a. Проведем спецификацию модели графическим методом. Поскольку необходимо найти зависимость объема товарооборота от числа работников, то в качестве Y – принимаем Объем товарооборота, X - Число работников.
Рисунок 2. Спецификация модели На основании поля корреляции можно выдвинуть гипотезу о том, что связь между всеми возможными значениями X и Y носит линейный характер. Для оценки параметров a и b - используют МНК (метод наименьших квадратов). b. Параметры уравнения регрессии. Выборочные средние:
Таблица 4. Расчет параметров модели
Используя формулы (6) и (7), получаем коэффициенты регрессии: b = 0.0192, a = -0.97. (b>0, следовательно связь прямая) Уравнение регрессии: y = 0.0192 x - 0.97, Величина коэффициента b говорит о том, что с ростом числа работников на 1 человека, объем товарооборота магазина будет увеличиваться на 0,0192 млн. руб. c. Теснота связи.
Среднеквадратическое отклонение:
Рассчитываем показатель тесноты связи. Таким показателем является линейный коэффициент корреляции, который рассчитывается по формуле:
В нашем примере связь между признаком Y и фактором X (по шкале Чеддока) весьма высокая. Кроме того, коэффициент линейной парной корреляции может быть определен через коэффициент регрессии b:
Незначительные отклонения в расчетных величинах возможны из-за округления величин.
d. Коэффициент детерминации. Подставив в уравнение регрессии соответствующие значения х, можно определить выровненные (модельные) значения результативного показателя y(x) для каждого наблюдения.
т.е. в 97.12 % случаев изменения х приводят к изменению y. Другими словами - точность подбора уравнения регрессии - высокая. Остальные 2.88 % изменения Y объясняются факторами, не учтенными в модели. Таблица 5. Расчет промежуточных величин для оценки качества модели
5. Критерий Фишера.
Табличное значение критерия со степенями свободы k1=1 и k2=6 (8-1-1), Fтабл = 5.99 Поскольку фактическое значение Fфакт > Fтабл, то коэффициент детерминации статистически значим (найденная оценка уравнения регрессии статистически надежна). 6. Ошибка аппроксимации. Оценим качество уравнения регрессии с помощью ошибки абсолютной аппроксимации. Средняя ошибка аппроксимации - среднее отклонение расчетных значений от фактических:
Ошибка аппроксимации в пределах 5%-7% свидетельствует о хорошем подборе уравнения регрессии к исходным данным. Поскольку ошибка меньше 7%, то данное уравнение можно использовать в качестве регрессии. 7. Проверка статистической значимости параметров. Несмещенной оценкой дисперсии возмущений является величина:
Стандартное отклонение случайной величины a:
Стандартное отклонение случайной величины b:
Поскольку 14.12 > 2.447, то статистическая значимость коэффициента регрессии b подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).
Поскольку 6.2 > 2.447, то статистическая значимость коэффициента регрессии a подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента). 8. Доверительный интервал для коэффициентов уравнения регрессии. Определим доверительные интервалы коэффициентов регрессии, которые с надежностью 95% будут следующими: (b – tтабл mb; b + tтабл mb) = (0.0192 - 2.447 • 0.00136; 0.0192 + 2.447 • 0.00136) = = (0.0158;0.0225) С вероятностью 95% можно утверждать, что значение данного параметра будет лежать в найденном интервале. (a – tтабл ma; a + tтабл ma) = (-0.9739 - 2.447 • 0.156; -0.9739 + 2.447 • 0.156) = = (-1.356;-0.5922) С вероятностью 95% можно утверждать, что значение данного параметра будет лежать в найденном интервале. 9. Коэффициент эластичности. Коэффициенты регрессии (в примере b) нежелательно использовать для непосредственной оценки влияния факторов на результативный признак в том случае, если существует различие единиц измерения результативного показателя у и факторного признака х. Для этих целей вычисляются коэффициенты эластичности и бета - коэффициенты. Средний коэффициент эластичности E показывает, на сколько процентов в среднем по совокупности изменится результат у от своей средней величины при изменении фактора x на 1% от своего среднего значения. Коэффициент эластичности находится по формуле:
В нашем примере коэффициент эластичности больше 1. Следовательно, при изменении Х на 1%, Y изменится более чем на 1%. Другими словами - Х существенно влияет на Y.
10. Интервальный прогноз. Точечный прогноз показателя
Далее вычисляется средняя стандартная ошибка прогноза
Строится доверительный интервал прогноза:
Задача 2. Имеются данные о количестве выпускаемой продукции в тыс. штук (x) и ее себестоимостью в у.е. (y).
Таблица 6. Исходные данные к Задаче 2.
1. Для характеристики зависимости у от х рассчитать параметры следующих функций: а) линейной; б) степенной; в) показательной; г) равносторонней гиперболы. 2. Оценить каждую модель через среднюю ошибку аппроксимации 3. Выбрать лучшую модель для прогноза.
Проведем спецификацию модели графическим методом.
Рисунок 3. Поле корреляции к Задаче 2.
Построим линейную и нелинейные регрессии и оценим их качество.
A. Линейная модель. Для расчета параметров a и b линейной регрессии y=a=b*x рассчитываем
Таблица 7. Расчет параметров линейной модели.
Уравнение регрессии: C увеличением количества выпускаемой продукции на 1 тыс., ее себестоимость снижается в среднем на 0,4671 у.е. Рассчитаем линейный коэффициент парной корреляции. Среднеквадратическое отклонение:
Связь обратная и весьма высокая. Определим коэффициент детерминации:
Вариация результата на 86% объясняется вариацией фактора x. Таблица 7. Расчет промежуточных величин для оценки качества линейной модели
Найдем величину средней ошибки аппроксимации
Рассчитываем F - критерий:
Fтабл = 4,7472. Так как Fфакт > Fтабл, уравнение регрессии значимо. B. Степенная модель. Построению степенной модели
Где Y=lg y, X= lg x, C= lg a. Для расчетов используем данные Таблицы 8. Таблица 8. Расчет параметров степенной модели.
Сумма Среднее Рассчитаем С и b:
Получим линейное уравнение: Выполнив его потенцирование, получим:
Подставляя в данное уравнение фактические значения x, получаем теоретические значения результата
Связь весьма высокая. Определим индекс детерминации:
Вариация результата на 99% объясняется вариацией фактора x.
Расчетные значения в среднем откланяются от фактических на 3,6 %. Таблица 9. Расчет величин для оценки качества степенной модели.
Рассчитываем F - критерий:
Fтабл = 4,7472. Так как Fфакт > Fтабл, уравнение регрессии значимо, статистически надежно.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 340; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.113.188 (0.083 с.) |
 свободный член
свободный член  экономического смысла не имеет.
экономического смысла не имеет. называется коэффициентом регрессии
называется коэффициентом регрессии 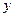 по
по  . Он показывает, на сколько единиц в среднем изменяется переменная
. Он показывает, на сколько единиц в среднем изменяется переменная  .
.







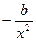



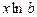



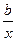





 - характеризует соотношение прироста результата и фактора для соответствующей формы связи.
- характеризует соотношение прироста результата и фактора для соответствующей формы связи. определяется путем подстановки в уравнение регрессии
определяется путем подстановки в уравнение регрессии 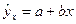 соответствующего прогнозного значения
соответствующего прогнозного значения  .
. , где
, где  .
.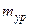

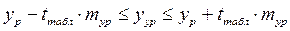 .
.
 ,
, 



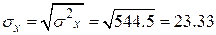 ,
, 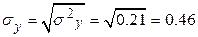
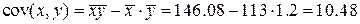


 =0,9712,
=0,9712,
 .
.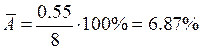
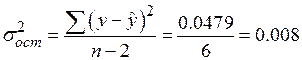 - необъясненная дисперсия (мера разброса зависимой переменной вокруг линии регрессии).
- необъясненная дисперсия (мера разброса зависимой переменной вокруг линии регрессии). - стандартная ошибка оценки (стандартная ошибка регрессии).
- стандартная ошибка оценки (стандартная ошибка регрессии).








 0.0192 x - 0.97 соответствующего прогнозного значения
0.0192 x - 0.97 соответствующего прогнозного значения 




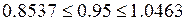
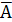 и F-критерий Фишера.
и F-критерий Фишера.
 ,
,  ,
,  ,
,  ,
,  .
.

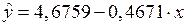 .
. ;
;  .
. ;
;  .
. .
. .
.

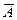 :
: .
.
 предшествует процедура линеаризации переменных. В примере линеаризация производится путем логарифмирования обеих частей уравнения:
предшествует процедура линеаризации переменных. В примере линеаризация производится путем логарифмирования обеих частей уравнения:



 .
.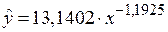 .
.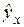 . По ним рассчитываем показатели: тесноты связи - индекс корреляции R и среднюю оценку аппроксимации
. По ним рассчитываем показатели: тесноты связи - индекс корреляции R и среднюю оценку аппроксимации  .
.
 .
.


