
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тест на обнаружение автокорреляции ⇐ ПредыдущаяСтр 9 из 9
Одной из предпосылок регрессионного анализа является независимость случайного члена в любом наблюдении от его значений во всех других наблюдениях. Если данное условие не выполняется, то говорят, что случайный член подвержен автокорреляции. В этом случае коэффициенты регрессии, полученные по МНК, оказываются неэффективными, хотя и несмещенными, а их стандартные ошибки рассчитываются некорректно. Автокорреляция обычно встречается при использовании данных временного ряда. Стационарные временные ряды, это ряды, вероятностные свойства которых не изменяются во времени. Стационарные временные ряды применяются, в частности, при описании случайных составляющих анализируемых рядов. Временной ряд yi (i = 1, 2, …, n) называется строго стационарным (или стационарным в узком смысле), если совместное распределение вероятностей n наблюдений y1, y2, …, yn такое же, как и n наблюдений
Тест Дарбина-Уотсона определяет наличие автокорреляции между соседними членами ряда. Выдвигается нулевая гипотеза об отсутствии корреляции первого порядка, т.е. H0: r =0, где r – коэффициент корреляции между двумя соседними случайными членами Еi и Еi-1; В качестве альтернативной гипотезы может выступать либо H1: r >0, либо H2: r < 0. Соответствующей оценкой коэффициента корреляции r является коэффициент автокорреляции остатков первого порядка, который при достаточно большом числе наблюдений имеет вид:
Введем величину Естественно, что в случае отсутствия автокорреляции выборочный коэффициент r 1 окажется не сильно отличающимся от нуля, а значение статистики d будет близко к 2. Близость наблюдаемого значения к нулю должна означать наличие положительной автокорреляции, к четырем – отрицательной. Тест Дарбина-Уотсона имеет один существенный недостаток – распределение статистики d зависит не только от числа наблюдений, но и от значений регрессоров xj (j =1, …, p). Это означает, что тест Д-У, вообще говоря, не представляет собой статистический критерий, в том смысле, что нельзя указать критическую область, которая позволяла бы отвергнуть гипотезу об отсутствии корреляции, если бы оказалось, что в эту область попало наблюдаемое значение статистики d. Однако, существуют два пороговых значения dВ и dН, зависящие только от числа наблюдений, числа регрессоров и уровня значимости, такие, что выполняются следующие условия.
Если фактически наблюдаемое значение d: 1. dB<d<4-dB, то гипотеза об отсутствии автокорреляции принимается; 2. dН<d<dB или 4- dB<d<4-dН, то вопрос об отвержении или принятии гипотезы остается открытым (область неопределенности критерия); 3. 0<d<4-dН, то принимается альтернативная гипотеза о положительной автокорреляции; 4. 4-dН<d<4, то принимается альтернативная гипотеза об отрицательной автокорреляции. Для d – статистики найдены dB и dН границы на различных уровнях значимости и помещены в таблицу. Недостатками критерия Д-У является: 1) Наличие области неопределенности критерия; 2) Критические значения d – статистики определены для объемов выборки не менее 15. В этом смысле при n = 6, 7, 8 результаты недостоверны даже для парной регрессии; 3) Методика расчета и использование критерия Д-У направлена только на выявление автокорреляции остатков первого порядка.
ПРИМЕР РЕШЕНИЯ ЗАДАЧИ Задание 5. Имеются данные об объемах потребления электроэнергии жителями региона в млн кВт*ч за 16 кварталов. (Таблица 24) Таблица 24. Исходные данные к Задаче 5.
Задание. Построить модель временного ряда. Решение. Нанесем значения
Рис.7. Спецификация модели временного ряда. По графику можно установить наличие приблизительно постоянной амплитуды колебаний. Это свидетельствует о возможности построения аддитивной модели временного ряда.
Определим коэффициент автокорреляции первого порядка. Он составит Это значение свидетельствует о слабой зависимости текущих уровней ряда от непосредственно предшествующих им уровней. Однако, как следует из графика, каждый следующий уровень Рассчитав коэффициент автокорреляции второго порядка. Продолжив расчеты, получим автокорреляционную функцию этого ряда (Таблица 25) Таблица 25. Коррелограмма временного ряда Задания 5.
Анализ значений автокорреляционной функции позволяет сделать вывод о наличии в изучаемом временном ряде сезонных колебаний периодичностью в четыре квартала, т.к. Рассчитаем компоненты аддитивной модели. Шаг 1. Проведем выравнивание исходных уровней ряда методом скользящей средней. Для этого: · просуммируем уровни ряда последовательно за каждые четыре квартала со сдвигом на один момент времени и определим условные годовые объемы потребления электроэнергии (столбец 3 таблицы 26); · разделив полученные суммы на 4, найдем скользящие средние (столбец 4 таблицы 26). Отметим, что полученные таким образом выравненные значения уже не содержат сезонной компоненты; · приведем эти значения в соответствие с фактическими моментами времени, для чего найдем средние значения из двух последовательных скользящих средних — центрированные скользящие средние (столбец 5 табл. 26).
Таблица 26. Расчет оценок сезонной компоненты аддитивной модели
· Шаг 2. Найдем оценки сезонной компоненты как разность между фактическими уровнями ряда и центрированными скользящими средними (столбец 6 таблица 26). Используем эти оценки для расчета значений сезонной компоненты S (таблица 27). Для этого найдем средние за каждый квартал (по всем годам) оценки сезонной компоненты Таблица 27. Расчет значений сезонной компоненты в аддитивной модели
Для данной модели имеем:
Определим корректирующий коэффициент:
Рассчитаем скорректированные значения сезонной компоненты как разность между ее средней оценкой и корректирующим коэффициентом k:
где i=1:4 Таким образом, получены следующие скорректированные значения сезонной компоненты: I квартал: II квартал: III квартал: IV квартал: Проверим условие равенства нулю суммы значений сезонной компоненты:
Занесем полученные данные в таблицу 27 для соответствующих кварталов каждого года. Шаг 3. Исключим влияние сезонной компоненты, вычитая ее значение из каждого уровня исходного временного ряда. Получим величины Т+ Е= Y— S (столбец 4 таблица 28). Эти значения рассчитываются за каждый момент времени и содержат только тенденцию и случайную компоненту. Таблица 28. Расчет выравненных значений T и ошибок E
Шаг 4. Определим компоненту Т данной модели. Для этого проведем аналитическое выравнивание ряда (Т + Е) аналогично парной регрессии.
Рис. 8. Выбор вида тренда. Для упрощения расчетов, выберем линейный тренд, т.к. его
Результаты аналитического выравнивания следующие: Константа………………………………………………..………….5,715416 Коэффициент регрессии……… ………………………………...0,186421 Стандартная ошибка коэффициента регрессии………………....0,015188 R-квадрат............................................................................................0,914971 Число наблюдений.............................................................................16 Число степеней свободы....................................................................14 Таким образом имеем линейный тренд: Подставив в это уравнение значения t = 1,...,16, найдем уровни T для каждого момента времени (столбец 5 таблица 28) Шаг 5. Найдем значения уровней ряда, полученные по аддитивной модели. Для этого прибавим к уровням T значения сезонной компоненты для соответствующих кварталов (столбец 6 таблица 28).
Шаг 6. В соответствии с методикой построения аддитивной модели расчет ошибки производится по формуле:
Численные значения абсолютных ошибок приведены в столбце 7 табл. 28. По аналогии с парной моделью регрессии для оценки качества построения модели или для выбора наилучшей модели можно применять сумму квадратов полученных абсолютных ошибок. Для данной аддитивной модели сумма квадратов абсолютных ошибок равна 1,10 (столбец 8 таблица 28). По отношению к общей сумме квадратов отклонений уровней ряда от его среднего уровня, равной 67,12, эта величина составляет чуть более 1,6%:
Следовательно, можно сказать, что аддитивная модель объясняет 98,4% общей вариации уровней временного ряда потребления электроэнергии за последние 16 кварталов.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ. Задачи для самостоятельного решения Задание 6. Имеются поквартальные данные по розничному товарообороту. Таблица 29. Исходные данные к Заданию 6.
Задание:
Задание 7. Имеются даны об объеме экспорта из Российской Федерации (млрд долл.) Таблица 30. Исходные данные к Заданию 7.
Задание:
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ. Провести эконометрическое исследование данных, характеризующих один объект за ряд последовательных моментов (периодов) времени. Построить модель (аддитивную или мультипликативную) временного ряда на основе реальных статистических данных, полученных из официальных источников статистической информации (Государственного комитета статистики РФ, международных финансовых организаций и др.).
*- По результатам проведенного эконометрического исследования подготовить научную статью для публикации в периодических научных изданиях. ЛИТЕРАТУРА: 1. Практикум по эконометрике: Учеб. пособие / И.И. Елисеева, С.В. Курышева, Н.М. Гордеенко и др.; Под ред. И.И. Елисеевой. – 2–е изд., перераб. и доп. – М.: Финансы и статистика, 2014. – 344 с. 2. Прикладная статистика. Основы эконометрики: Учебник для вузов: В 2 т. 2–у изд., испр. – Т. 2: Айвазян С.А. Основы эконометрики. – М.: ЮНИТИ–ДАНА, 2015. – 432 с.
3. Чураков Е.П. Прогнозирование эконометрических временных рядов: учеб. пособие / Е.П. Чураков. – М.: Финансы и статистика, 2014. – 208 с. 4. Эконометрика: учеб. / под ред. д–ра экон. наук, проф. В.С. Мхитаряна. – М.: Проспект, 2014. – 384 с. 5. Эконометрика: учеб. / под ред. И.И. Елисеевой. – М.: Проспект, 2015. – 288 с. 6. Эконометрика: Учебник/И.И. Елисеева, С.В. Курышева, Т.В. Костеева и др., Под ред. И.И. Елисеевой. – 2–е изд., перераб. и доп. – М.: Финансы и статистика, 2015. – 576 с.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 468; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.46.36 (0.058 с.) |
 при любых n, i, t. Другими словами, свойства строго стационарных рядов yi не зависят от i, т.е. от момента времени. Напомним, что в случае пространственной выборки отсутствие автокорреляции постулируется.
при любых n, i, t. Другими словами, свойства строго стационарных рядов yi не зависят от i, т.е. от момента времени. Напомним, что в случае пространственной выборки отсутствие автокорреляции постулируется.
 . Очевидно,
. Очевидно, 
 Рис. 6. Границы значимости.
Рис. 6. Границы значимости.




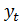 на график.
на график.



 =0,983.
=0,983. .
.




 = 0,581;
= 0,581; =
=  1,977;
1,977; =
= 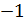 ,294;
,294; = 2,690.
= 2,690.

 (T+S)
(T+S)


 также имеет высокое значение.
также имеет высокое значение. .
.




