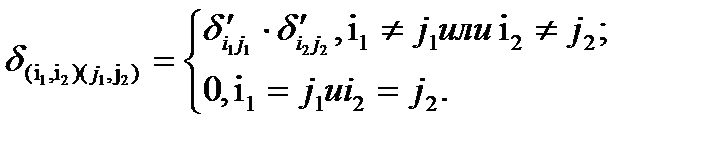Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Способы представления множеств.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Понятие множества. Понятие «множество» относится к числу фундаментальных неопределяемых понятий в математике. Множеством называется любая определенная совокупность объектов. Объекты их которых состоит множество называется элементами. Элементы множеств различны. Множества обычно обозначаются прописными буквами лат. алфавита, а элементы – строчными. П. N – множество натуральных чисел P – множество простых чисел Z – множество целых чисел R – множество вещественных чисел Если объект х принадлежит множеству, то он является элементом множества и обзначается хÎМ. Если объект х не принадлежит множеству, то он не является элементом множества и обозначается х ÏМ. Æ - пустое множество, множество, которое не включает в себя элементов.. Обычно элементы множества выбираются из одного достаточно широкого множества U, которое называется универсумом. Множества бывают конечные и бесконечные. Число элементов в множестве М называется мощностью множества и обозначается çМç. êÆú êí0ýú = 1 êí1,2,3,4,5ýú = 5 Если мощность множества А = мощности множества В, то говорят, что множества равномощны.
Способы представления множеств. 1)способ перечисления элементов; íа1,а2,а3,…аný При помощи перечисления можно задавать только конечные множества, если способ перечисления использовать для перечисления бесконечных множеств, то форма записи не должна вызывать разночтений. 2) способ описания элементарных множеств путем задания их свойств: Р:íхïх – «отличник»ý; К:íхïх – «четное число»ý 3) способ описания множества при помощи порождающей процедуры Порождающая процедура – это способ получения элементов множества из уже имеющихся или из других объектов. Элементами множества будут считаться все объекты, которые могут быть получены при помощи порождающей процедуры. А:ímïm=2k, kÎN ý 4)способ описания множеств при помощи функции предикат. Характеристически предикат – это некоторое логическое условие, выражение в фолме логического утверждения, которое принимает значение «истина» или «ложь». М:íхïх>5 ý Р(х) – в скобках указывается аргумент функции предикат. С помощью перечисления можно задавать конечные множества. Бесконечные множества удобно задавать характеристическим предикатом или порождающей процедурой.
Операции над множествами. Выполнение операций над множествами – это способ конструирования новых множеств из уже имеющихся. 1. Сравнение множеств множество Х называется подмножеством множества Y, если каждый элемент множества Х принадлежит множеству Y. ХÌ Y: хÎХÞхÎY Х – подмножество множества Х. Если Х является подмножеством множества Y и множества не равны, то говорят, что Х – собственное подмножество множества Y. Замеч. если требуется различать собственные и несобственные, то для обозначения собственных множеств используется С, для несобственных - С 2.Равенство множеств множество Х и Y равны, если они являются подмножествами друг друга. Х=У: ХÌ Y и Y ÌХ. 3.Объединение множеств Объединение множеств Х и Y называется множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множеств XÈY:{xïxÎX или xÎY}
4. Пересечение множеств Пересечение множеств Х и Y называется множество, состоящие из тех и только тех, которые принадлежат и множеству X и множеству Y. XÇY:{xïxÎX и xÎY} 5. Разность множеств Разность множеств Х и Y (Х¤Y) называется множества всех тех элементов множества Х, которые не принадлежат множеству Y. Х¤Y:{xïxÎX и xÏХ} 6. Симметрическая разность (X∆Y)=(XÈY)/(XÇY) 7. Дополнение
Разбиения и покрытия. Одной из операций над множествами является разбиением множеств на систему подмножеств. Рассмотрим множество М и систему подмножеств m={x1,x2…xn} Система подмножеств называется разбиением множества М если: 1. любое множество х из m является подмножеством множества М: "хÎ m х ÌМ 2. любые 2 подмножества xi и xj, принадлежащие m не пересекаются xi Ç xj=Æ 3)объединение всех множеств xi, принадлежащих mравно множеству М. xiÎmÈ xi=М Семейство m называются покрытием М, если каждый элемент множества М принадлежит хотя бы одному из множеств xi.
Функциональное отношение. Отношения АÌХ´У будем называется функциональным, если все его элементы (упорядоченные пары) имеют различные первые координаты. Х={х1 х2 х3 х4 х5} У={у1 у2 у3} АÌХ*У={(x1 у1), (х1 у2) (х1 у3) (х2 у1)…} Функциональное отношение из множества Х в У называется функцией и обозначается: f:X®Y Обычно для задания функции используют префиксную запись: y=f(x), х-аргумент, у – значение. Пусть задана f(x) f:X®Y Область определения функции: fx={x| $y f(x)=y} fy={y| $x y=f(x)} Если обл. определения f(x) является вся мн. Х, то функция называется тотальной. fxÌХ – частичная. Пусть f:X®Y, а f1:Q®Y QÌX Причем для "хÎQ f и f1 значения сходятся, тогда функцию f1 называют схождением функции f на множестве Q, а функцию f – продолжением функции f1 на мн. Х. Функции алгебры логики. Пусть Е2={0, 1}. Булевой функцией f наз. отображение вида f: E2n®E2 или f=f(x1, x2, …xn). Всевозможные упорядоченые последовательности из нулей и единиц наз. набором. |E2n|=2n. Область определения ф-ции конечна, поэтому ее удобно описывать с помощьб таблиц истиности. Каждый набор x1, x2, …xn можно рассматривать как некоторое двоичное число. будем предполагать, что наборы x1, …xn упорядочены в таблице по возрастанию (как двоичные числа). Каждый последующий набор получается из предыдущего прибавлением двоич. единицы (00…1). Последний столбец табл. истиности обозначается Nf или af. Бул. ф-ция от n переменных однозначно определяется столбцом своих значений. Длинна столбца 2n и каждый эл. принимает одно из двух значений. Поэтому число бул. функций равно 22^n. Если мн-во всех бул. функций Р2(n), то |Р2(n)|=22^n. Ф-ции 2n и 22^n быстро растут с ростом n и поэтому распознование св-в бул. ф-ций полным перебором строк таблицы истиности и полным перебором бул. ф-ций от n переменных на практике возможно только для небольших n. Перебор строк – для n£40. Перебор бул. ф-ций – для n£6. Этот результат не зависит от быстродействия машин. Переменную xi наз. несуществественной (фиктивной) для ф-ции f(x1, x2, …xn), если ее значение не влияет на значение ф‑ции. Пусть a=(a1, a2,…ai-1, 0, ai+1,… an) и a’=(a1, a2,…ai-1, 1, ai+1,… an). Тогда a и a’ – соседние наборы по переменной ai, понятно, что хi несущественна для f, если "a и a’ f(a)=f(a’). В противном случае переменную будем наз. существенной. Удаление фиктивной переменной осуществляется след. образом: из каждой пары соседних наборов оставляем один, а второй удаляем и даляем столбец, соот-щий фиктивной переменной. Операция введения фиктивной переменной осущ. в обратном порядке. Две бул. ф-ции наз. равными, если одна из них получается из другой путем добавления или удаления фиктивной переменной. Среди бул. ф-ций выделяются элементарные бул. ф-ции: 1)константы: 1, 0; 2)тождественная ф-ция: х; 3)отрицание:ùх; 4)
Задание функций алгебры логики. Булевую функцию n-переменных можно задать таблицей истинности:
В левой части таблицы истинности записываются все 2n возможных значений переменных, в правой части зап. значения функций на этих наборах. Наборы, на которых функция принимает значение 1 наз. единичными, а те – на которых 0 – нулевыми. Обычно наборы переменных располагают в лексикографическом порядке, который совпадает с порядком возрастания наборов, рассматриваемых как двоичные числа. Число булевых функций от n переменных быстро возрастает с увеличением n.
Примеры логических функций. Функции одной переменной:
Ф-ция 0 и 1 задает константы, поэтому для них х – несущественная переменная. Тождественная ф-ция возвращает х, а обратная – обратное значение х. Функции 2-х переменных
Представление булевых функций формулами. Примеры. Функции называются выражением, описывающие суперпозицию элементарных функций. Суперпозицией будем называть функцию f, полученную в результате подстановок функций друг в друга и переименования переменных. Переменные, от которых зависит функция называют формулами имеющими глубину 0. f(x1x2). Функция зависящая от переменных формулой глубины 1. Соответственно функция f(f1,f2..fn) будет иметь глубину k если она зависит от функций глубины k-1. Для записи формул используют знаки операций(конъюнкция, сложение по модулю 2, Стрелка Пирса, импликация и тд). Обычно для булевых функций используется инфиксная запись. Функция каждому набору аргументов ставит в соответствие значение и следовательно может служить способом описания функции. Табличное представление функции является единственным способом. Для задания функции формулой можно использовать различные записи. Класс монотонных функций. М – класс монотонных ф-ций. Пусть a=(a1,…,an) и b=(b1,…, bn). Набор a меньше набора b (a<b), {(< – такой треугольничек)} если a1£b1, a2£b2,…,an£bn. Например: (1001)<(1011). < – рефликсивно, транзитивно, антисиметрично, т.е. это отношение частичного порядка, но в общем случае не линейного порядка. Ф-ция f наз. монотонной, или всегда из того, что a<b следует f(a)£f(b). входят: 0, 1, x, &, Ú. невходят: Øx, ®, , ¯. Для проверки ф-ции на монотонность необходимо проверить, что f(a)£f(b) для всевозможных пар сравнимых наборов. Класс мон. ф-ций замкнут: [M]=M. Соотношение a<b индуцирует это же соотношение на всевозможных поднаборов a и b. (aj1, aj2, …,ajij)<(bj1, bj2, …,bjij). Пусть gi=fj(aj1, aj2, …,ajij), di=fj(bj1, bj2, …,bjij) тогда из того, что fjÎM, gi£dj (j=1,k), т.е. g<d но f0ÎM т.е. f0(g)£f0(d), а, значит Ф(g)£Ф(d). ч.т.д. Лема о немонотонных ф-циях: Если ф-ция f немонотонна, то из нее путем подстановки вместо переменных констант и тождественной ф-ции можно подставить отрицание. Пусть fÏM т.е. $a<b: f(a)<f(b), поэтому f(a)=1, f(b)=0. Покажем, что найдутся два соседних набора (по некоторой переменной) a и b такие, что a<b, а f(a)>f(b). Предположим обратное: пусть a<b и они отличаются, например, по первым t переменным. a=(0, 0, …, 0, at+1,…,an) b=(1, 1, …, 1, bt+1,…, bn) По a и b построим последовательность наборов a(0)=a, a(1) – соседний с a(0) по 1-й переменной, a(2) – по 2-й переменной и т.д., a(t)=b. a=a(0)<a(1)<…<a(t)=b, причем f(a(0))>f(a(t)), поэтому в этой последовательности найдутся два соседних набора a(i)<a(i+1), а f(a(0))>f(a(i+1)). Поэтому будем предпологать, что a и b – два соседних набора, для которых нарушается монотонность. Эти наборы можно найти по таблице истинности. Построим ф-цию j(x)=(a1,…,ai-1,x,ai+1,…,an) (наборы и соседние по х). j(0)=(a1,…,ai-1,0,ai+1,…,an)=f(a)=1 j(1)=(a1,…,ai-1,1,ai+1,…,an)=f(b)=0 т.е. j(x)=Øx ч.т.д. Класс линейных функций. L – класс ленейных ф-ций. Ф-ция f(x1,…xn) наз. линейной, если ее представление в виде полинома Жегалкина имеет вид: f(x1,…xn)=a0Åa1x1Åa2x2Å…Åanxn. Слогаемые ai×xi наз. линейными, а все остальные – нелинейными. линейные: 0, 1, x, Øx=xÅ1, Å. нелинейные: &, Ú, ®, , ¯. Каждая линейная ф-ция однозначно определяется своими коэфициэнтами, поэтому |L|=2n+1. т.к. суперпозиция линейных ф-ций – линейная ф-ция, то класс линейных ф-ций замкнут: |L|=L. Лема о нелинейных ф-циях: Если ф-ция нелинейна, то из нее путем подстановки вместо переменных, констант, тождественной ф-ции и отрицания самой ф-ции можно получить коньюнкцию. Док-во: Пусть fÏL. Тогда в ее представлении в виде полинома Жегалкина имеется наименьшее слагаемое. Будем предполагать, что в это слогаемое входят переменные x1 и x2. Тогда $(a3, a4,…,an): f(x1, x2, a3, a4,…,an)=x1×x2Åa×x1Åb×x2Åg. (в противном случае, переменные x1, x2 были бы фиктивными). j(x1, x2)= x1×x2Åa×x1Åb×x2Åg. По ф-ции построем ф-цию S: S(x1, x2)=j(x1Åb, x2Åa)Åa×bÅg. Можно показать, что S(x1, x2)=x1&x2.
Из таблицы видно, что основные замкнутые классы попарно не совпадают. Полином Жегалкина. Теорема. Полиномом (многочленом) Жегалкина от п переменных называется функция f(x1, x2, …, xn)=С0+С1х1+C2x2+…+Cnxn+C12x12+…+C12…nx1x2..xn Теорема. Любая функция п переменных может быть представлена полиномом Жегалкина и это представление единственно. Доказательство. Любая функция f(x1, x2, …, xn) имеет свою таблицу истинности. Запишем сначала данную функцию в виде полинома Жегалкина с неопределенными коэффициентами. Затем по очереди подставляем всевозможные наборы переменных и находим коэффициенты. Легко видеть, что за каждую подстановку находим только один коэффициент. Так как число наборов равно числу коэффициентов (и равно 2п), отсюда следует утверждение теоремы. Доказательство этой теоремы показывает, как по таблице истинности построить полином Жегалкина. Имеется 2-й способ нахождения полинома Жегалкина для функций, заданных в виде ДНФ. Этот способ основан на том, что х+1 =. Если функция задана в виде ДНФ, то сначала убираем дизъюнкцию, используя при этом правило де Моргана, а все отрицания заменяем прибавлением единицы. После этого раскрываем скобки по обычным правилам, при этом учитываем, что четное число одинаковых слагаемых равно нулю (так как х+ х = 0), а нечетное число одинаковых слагаемых равно одному такому слагаемому. Полнота. Система функций F называется функционально полной если любая ее функция может быть представлена формулой над F, т.е. в виде суперпозиции функций системы F. F={конъюнкция, дизъюнкция, отрицание} – является функционально полной, так как любую булевую функцию можно представить в виде конъюнкций, дизъюнкций и отрицаний. Функционально полной будет любая система F, функции которой можно выразить через конъюнкции, дизъюнкции и отрицания. Для любой логической функции можно записать, заменив в ней все операции, отличные от конъюнкции, дизъюнкции и отрицания на эти функции. F={конъюнкция, отрицание} – является полной так как по закону де Моргана и двойному отрицанию можно получить дизъюнкцию. С точки зрения функциональной полноты система функций F={конъюнкция, дизъюнкция, отрицание} можно считать избыточной, так как либо конъюнкцию либо дизъюнкцию можно выразить через отрицание и дизъюнкции или конъюнкцию. Однако Логические исчисления. Особенностью человеческого мышления является способность к логическим рассуждениям, когда, имея некоторые предпосылки, истинность которых проверена на практике, мы получаем до утверждения, которые тоже истинны. Опыт древних ученых был обобщен Аристотелем, который сформулировал конкретные виды рассуждений. Аристотель рассмотрел 4 вида категорических рассуждения: 1. все А обладают свойством В. 2. некоторые А обладают свойством В. 3. все А не обладают свойством В. 4. некоторые А не обладают свойством В. Были зафиксированы все случаи, когда из посылок такого вида выводятся предпосылки одного из этих видов. (Пример: 1)все люди смертны, 2) Сократ – человек. Вывод – Сократ смертен) Утверждения получили названия силлогизмы Аристотеля. Наиболее часто используемые логические исчисления – это исчисления высказываний,. исчисления предикатов. Высказывания. Формулы. Высказывания Элементы логических рассуждений – это утверждения, которые либо истинны, либо ложны. Такие утверждения называются высказываниями. Высказывания называются простыми, если они касаются 1 объекта. Обычно они обозначаются пропозициональными переменными, которые могут быть либо истинными, либо ложными. Если пропозициональные переменные соединены между собой логическими связями, то получаем сложные высказывания (составные).
Пример: если "холодно" и "идет дождь", то "одеться тепло" и "взять зонт". Формула Формула – это правильно построенное пропозициональное высказывание. Для исчисления высказываний справедлива след. таблица истинности.
Исчисление высказываний. Исчисление высказываний – это формальная теория, в которой присутствуют: 1) алфавит: - связки, ® - служебные символы, - пропозициональные переменные х1, х2… хn 2) формулы: - переменные - если А и В – формулы, то А и А® В тоже формулы. 3) аксиомы А1: А® (В®А) А2… А4 4) правило логического вывода А, А®В В Modus ponens Читается так: формула В выводится из формулы А и А®В по правилу вывода Modus ponens. Modus ponens – правило от деления. А и В – любые формулы. Таким образом, множество аксиом бесконечно и задаются несколькими видами схем. Понятие предиката. Предикат (n -местный, или n -арный) — это функция с областью значений {0,1} (или «Истина» и «Ложь»), определённая на n -й декартовой степени множества M. Таким образом, каждую n -ку элементов M он характеризует либо как «истинную», либо как «ложную». Предикат можно связать с математическим отношением: если n -ка принадлежит отношению, то предикат будет возвращать на ней 1. Предикат — один из элементов логики первого и высших порядков. Начиная с логики второго порядка, в формулах можно ставить кванторы по предикатам. Предикат называют тождественно-истинным и пишут: P если на любом наборе аргументов он принимает значение 1. Предикат называют тождественно-ложным и пишут: P если на любом наборе аргументов он принимает значение 0. Предикат называют выполнимым, если хотя бы на одном наборе аргументов он принимает значение 1. Так как предикаты принимают только два значения, то к ним применимы все операции булевой алгебры, например: отрицание, импликация, конъюнкция, дизъюнкция и т. д. Например, обозначим предикатом EQ(x, y) отношение равенства («x = y»), где x и y принадлежат множеству вещественных чисел. В этом случае предикат EQ будет принимать истинное значение для всех равных x и y. Более житейским примером может служить предикат ПРОЖИВАЕТ(x, y, z) для отношения «x проживает в городе y на улице z» или ЛЮБИТ(x, y) для «x любит y», где множество M — это множество всех людей. Исчисление предикатов. Исчисление предикатов производится в соответствии со следующими правилами: 1. аксиомой исчисления высказываний 2. предикатными аксиомами 3. "х F(х)®F(y) F(x)®$y F(y) Правило логического вывода 1. Правило modus poneus 2. Правило обобщения 3. Правило существования Обходы графов. Обход графов – это некоторое систематизированное перечисление его вершин (и/или ребер). Наибольший интерес представляют обходы, использующие локальную информацию о графе (матрицу смежности, инцидентности). Среди всех обходов наиболее известны: обходы в ширину и в глубину Для реализации обходов в глубину используется структура стэк; в ширину – очередь. Степени вершин графа. Если же неориентированный граф, то количество ребер, инцидентных вершине называется локальной степенью или степенью вершины например степень вершини обозначается p(v) p(1)=3 p(2)=2. Если в графе степени вершины конечны, то граф назвается локально конечным. Если для графа заданого матрицей инцидентности или матрицей смежности,то степень вершин можно определить след образом: p(Vj)=Sвверху m,внизу i=1 Eij. Висячая вершина – вершина степени 1. Висячее ребро – ребро соответствующее висячей вершине. Изолированная вершина имеет степень 0. Операции с частями графа. Частью HÌG (часть Н графа G) называется граф Н, если множество его вершин содержится в множестве вершин графа G, а множество ребер графа Н является подмножеством множества вершин графа G. Если множество вершин графа А и В совпадают то такой подграф называют суграфом. Подграфом G(U) графа G с множеством вершин U, являющихся подмножество множества вершин V, называется часть, которой принадлежат все ребра графа V с обоими концами из множества U Дополнение Н части Н будем определять множество всех ребер графа G не принадлежащих Н. Сумма: V(H1ÈH2)=V(H1) ÈV(H2) E(H1ÈH2)=E(H1) ÈE(H2) Разность: V(H1ÇH2)=V(H1) ÇV(H2) E(H1ÇH2)=E(H1) ÇE(H2) Две части графа Н1 и Н2 не пересекаются по вершинам, еслит они не имеют общих вершин. Сумма частей Н1 и Н2 не пересекающихся по вершинам называется прямой суммой. Маршруты, цепи, циклы. Маршрутом в графе G называется конечная или бесконечная последовательность ребер e1,e2,…,en, что каждые 2 соседние ребра имеют общую инцидентную вершину. Одно и то же ребро может встречаться в маршруте несколько раз. Маршрут называется открытым, незамкнутым, если его концевые вершины различны, иначе он называется замкнутым. Число ребер в маршруте называется длиной маршрута. Если начальная и конечная вершины совпадают то он называется цикличным. Маршрут называется цепью, если каждое ребро встречается не более 1-го раза и простой цепью, если любая вершина инцидентна не более чем 2-м ребрам. Цикличный маршрут называется циклом, если он является цепью и простым циклом, если он является простой цепью. Связные компоненты графа. Две вершины Vi и Vj называются связными в графе G, если в нем существует маршрут для которого Vi и Vj являются началом и концом. Граф G назывется связным, если каждая пара его вершин явл. связной, иначе граф называется не связным. Если вершина V графа G связана с какой-либо другой вершиной, то она связана сама с собой. Отношение связности 2-х вершин, заданное на множестве обладает свойствами рефлексивности, симметричности и транзитивности. Проверить или показать, каким образом отношение связности является отношением эквивалентности. Следовательно определяет разбиение мн. вершин графа на непересекающиеся подмножества. Вершины одного и того же множества связаны между собой, а вершины различных мн. – не связаны, поэтому в графе G нет ребра, которое бы имело концы в вершинах из разных множеств. Расстояния в графе. Пусть G – неориентированный граф, v¢ и v² - любые две его вершины. Тогда существует связывающая их простая цепь М (е1,е2,…, еq). Если количество q ребер этой цепи – не минимальное из возможных, то существует цепь М¢ (е¢1,е¢2,…, е¢q¢), связывающая v¢ и v² и имеющая меньшее число ребер. Если М¢ не минимально, то можно найти связывающую v¢ и v² цепь с еще меньшим количеством ребер и тд. Однако этот процесс уменьшения числа ребер можно повторить не более q раз, так как это число каждый раз уменьшается не меньше ем на единицу. Поэтому существует связывающая v¢ и v² цепь М~(е~1,е~2,…, е~p) с минимальным количеством ребер р. Минимальная длина простой цепи с началом v¢ и концом v² называется расстоянием d(v¢,v²) между этими вершинами. Считая каждую вершину v неориентированного графа связной с самой собой, мы по существу ввели нулевые маршруты, не содержащие ребер, с началом и концом в любой вершине vÎG. В соответствии с этим расстояние d (v,v) между вершиной v и ею самою равно 0. Для любой пары v¢,v²ÎG различных вершин d(v¢,v²)>0, т.к. связывающая эти вершины цепь состоит хотя бы из одного ребра. Расстояние d(v¢,v²) удовлетворяет аксиомам метрики: 1) d(v¢,v²)³0, причем d(v¢,v²)=0, когда v¢=v²; 2) d(v²,v¢)= d(v¢,v²); 3) справедливо неравенство треугольника: d(v¢,v²)+d(v²,v²¢)³d(v¢,v¢²). В особом доказательстве нуждается только последнее свойство. Пусть M¢ (v¢,v²) и М² (v²,v¢²) – минимальные простые цепи, связывающие v¢ с v² и v² с v¢². Тогда последовательность ребер М, в которой сначала идут все ребра цепи M¢, а затем ребра цепи M², - это маршрут, связывающий v¢ и v¢² и имеющий длину d(v¢,v²)+d(v²,v²¢). Как показано ранее, если этот маршрут не является простой цепью, то можно найти более короткую цепь М~, связывающую v¢ и v¢². Поэтому во всяком случае минимальная связывающая эти вершины цепь имеет длину, не превосходящую d(v¢,v²)+d(v²,v²¢). Произведение графов. Прямое произведение графов. Прямые произведения графов. Пусть даны графы G1и G2 с множествами вершин V1и V2. У прямого произведения этих графов F = G1×G2 множеством вершин является прямое произведение V = V1×V2. Ребра произведения могут быть определены различными способами. При одном из определений в произведении Fграфов G1и G2ребро Чаще всего используется третье определение, согласно которому ребро
Тогда матрица смежности прямого произведения графов G1и G2 при таком определении равна
Аналогично определяется прямое произведение любого множества графов.
Эйлеровы циклы. Цикл графа G, содержащий все его рёбра, наз. эйлеровым. Граф, имеющий эйлеров цикл наз. эйлеровым. Терорема. Для каждого связного графа G следующие условия эквивалентны: 1. G – эйлеров граф. 2. Каждая вершина графа G имеет чётную степень. 3. Мн-во рёбер графа можно разбить на простые циклы, т.е. U=Èki=1 ui (ui Çuj=Æ, (i¹j), ui=Æ). Доказательство. Пусть G – эйлеров граф. Покажем, что каждая вершина имеет чётную степень. Каждая вершина простого цикла имеет степень 2. Поэтому, если в графе G существует эйлеров цикл, то каждая вершина должна иметь чётную степень. Пусть каждая вершина имеет чётную степень. Выбираем произвольную вершину графа i1 и движемся от неё по ребру к смежной вершине i2, и т.д. каждый раз выбирая новое ребро. Т.к. граф связен, число рёбер в графе конечно и войдя в вершину по некоторому ребру мы можем выйти по другому, то через некоторое число шагов какая-то вершина ik повторится. Тогда i1,i2,…,ik,i1 образует простой цикл в исодном графе (u1). Удалим рёбра этого цикла из исходного графа. Новом графе каждая не изолированя вершина имеет чётную степень, поэтому процедуру выделения простых циклов можно применять к каждой компоненте связности, отличной от изолированой вершины. Через некоторое число шагов мы получим исх. разбиение. Пусть закдано разбиение U=Èki=1 ui. Покажем, что $ эйлеров цикл. Т.к. G – связный граф, то найдутся два простых цикла имеющих общую вершину эти два цикла можно объеденить (склеить) в один цикл. Пусть u’ и u’’ имеют общую вершину k. u’=(j1,j2,…,jl-1,k,j1+1,…,jm,j1), u’’=(t1,t2,…,td-1,k,td+1,…,tf,t1), u*=(j1,j2,…,jl-1,k,td-1,…,t1,tf,tf-1,…,td+1,k,j1+1,…,jm,j1). Число циклов при этом уменьшиться на еденицу. Повторяя процедуру склеивания, в итоге получим один цикл, содержащий все рёбра исходного графа – эйлеров цикл, ч.т.д. Док-во данной теоремы можно использовать в качестве алгоритма при построении эйлерового цикла, если он существует. Теорема Эйлера. Теорема: Граф называется Эйлоровым тогда и только тогда, когда он является связным и степени всех его вершин являются четными. Необходимость: В несвязанном графе каждый цикл принадлежит какой-либо его мвязанной части, т.е. не проходит через все его ребра (кроме случая, когда все компоненты связности графа, кроме одной, - изолированные вершины). Кроме того, каждый раз, когда эйлеров цикл приходит в какую-нибудь вершину, он должен выйти из нее по другому ребру, т.е. инцидентные вершинам ребра можно разбить на пары соседних в эйлеровом цикле. Исключением являются ребра, инцидентные началу эйлерова цикла, совпадающему с его концом. Сначала цикл выходит из этой вершины по какому-либо ребру. Затем он, возможно, несколько раз возвращается в эту вершину, каждый раз входя по новому ребру и выходя так же по новому, но другому ребру. В конце концов он возвращается в исходную вершину по не затронутому ранее ребру. Таким образом, и в этом случае инцидентные этой вершине ребра также распадаются на пары соседних в эйлеровом цикле, но одна из этих пар состоит из ребра, проходимого в начале процесса, и другого, замыкающего этот процесс. Достаточность: Пусть G – конечный связный граф с четными степенями всех вершин. Начнем построение эйлерова цикла с поизвольной вершины v графа G. каждый раз, когда мы добавляем к маршруту новое ребро и приходим в новую вершину, число свободных ребер в этой вершине изменяется на единицу. Если до этого оно было четным, то теперь оно становится нечетным и не может оказаться нулем. После ухода из этой вершины число свободных инцидентных ей ребер уменьшается еще на 1 и вновь становиться четным. Исключением является свободная вершина, у которой после начала процесса число свободных ребер нечетно и остается нечетным после каждого возвращения в эту вершину и ухода из нее. Описанный ранее процесс построения цикла может закончиться лишь в той вершине, откуда он начинался, но при этом не обязательно, чтобы он проходил через все ребра графа. Принадлежащие
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 1001; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.62.10 (0.011 с.) |

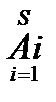 =A1ÈA2ÈA3È…ÈAs (общий случай)
=A1ÈA2ÈA3È…ÈAs (общий случай) :{xïxÏX}
:{xïxÏX}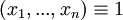

 имеется тогда, когда в графе G1есть ребро
имеется тогда, когда в графе G1есть ребро  или в графе G2 —
или в графе G2 — 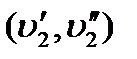 . В другом определении для этого требуется существование обоих этих ребер. В первом случае элементы матрицы смежности определяются формулой
. В другом определении для этого требуется существование обоих этих ребер. В первом случае элементы матрицы смежности определяются формулой 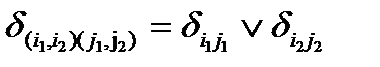 во втором
во втором 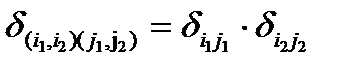 . Таким образом, в обоих случаях матрица смежности произведения является тензорным произведением матриц смежности сомножителей, но в первом случае произведение элементов матрицы понимается как логическая сумма
. Таким образом, в обоих случаях матрица смежности произведения является тензорным произведением матриц смежности сомножителей, но в первом случае произведение элементов матрицы понимается как логическая сумма  (или), а во втором -— как логическое (и обычное) произведение (и).
(или), а во втором -— как логическое (и обычное) произведение (и). , а в графе G2 есть ребро
, а в графе G2 есть ребро 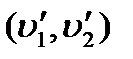 , а
, а 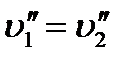 . Пусть
. Пусть 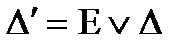 , где E — единичная матрица, а
, где E — единичная матрица, а  — матрица смежности рассматриваемого графа:
— матрица смежности рассматриваемого графа: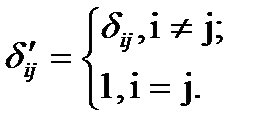

 , т.е.
, т.е.