Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интерпретация формулы. Теорема.
Рассмотрим А(х1, х2… хn) некоторую пропозициональную формулу, при этом х1, х2… хn – пропозициональные переменные, образующие конкретный набор значений, приписанный переменным х1, х2… хn называется интерпретацией формулы А. Формула может быть истинной при одной интерпретации и ложной – при другой. А(х1, х2… хn) ® Формула, которая является истинной при некоторой интерпретации, называется выполнимой. Формула, которая истинна при всех возможных интерпретациях, называется общезначимой ил тавтология. Формула, которая является ложной при всех возможных интерпретациях, называется невыполнимой или противоречием. АÚ А - тавтология А и А - противоречие А® А – выполнение
Теорема. Пусть А – некоторая формула, тогда: 1) если А – противоречие, то А – тавтология и наоборот. 2) если А – тавтология, то А – противоречие и наоборот. 3) если А – тавтология, то неверно, что А – противоречие, но не наоборот. 4) если А – противоречие, то неверно, что А – тавтология, но не наоборот. Теорема. Если формулы А и А® В тавтологии, то формула В – тавтология. Док. докажем методом от противного. I(B)=F, тогда I(A)=T, I(А® B)=F – противоречие условию. Посылка неверная, значит I(B)=T. Теорему доказано. Логическое следование и логическая эквивалентность. Говорят, что логическая формула В следует из формулы А, если формула В имеет значение "истина" при всех интерпретациях, при которых формула А имеет значение "истина" Говорят, что формулы А и В логически эквивалентны ( Теорема
Док-во: Для доказательства строится таблица истинности для правой и левой части и показывается, что они эквивалентны при любых интерпретациях.
Логические эквивалентности. Доказательство. Теорема Если A, B, C – любые логические формулы, то имеет место следующие логические эквивалентности:
Исчисление высказываний.
Исчисление высказываний – это формальная теория, в которой присутствуют: 1) алфавит: - связки, ® - служебные символы, - пропозициональные переменные х1, х2… хn 2) формулы: - переменные - если А и В – формулы, то А и А® В тоже формулы. 3) аксиомы А1: А® (В®А) А2… А4 4) правило логического вывода А, А®В В Modus ponens Читается так: формула В выводится из формулы А и А®В по правилу вывода Modus ponens. Modus ponens – правило от деления. А и В – любые формулы. Таким образом, множество аксиом бесконечно и задаются несколькими видами схем. Понятие предиката. Предикат (n -местный, или n -арный) — это функция с областью значений {0,1} (или «Истина» и «Ложь»), определённая на n -й декартовой степени множества M. Таким образом, каждую n -ку элементов M он характеризует либо как «истинную», либо как «ложную». Предикат можно связать с математическим отношением: если n -ка принадлежит отношению, то предикат будет возвращать на ней 1. Предикат — один из элементов логики первого и высших порядков. Начиная с логики второго порядка, в формулах можно ставить кванторы по предикатам. Предикат называют тождественно-истинным и пишут: P если на любом наборе аргументов он принимает значение 1. Предикат называют тождественно-ложным и пишут: P если на любом наборе аргументов он принимает значение 0. Предикат называют выполнимым, если хотя бы на одном наборе аргументов он принимает значение 1. Так как предикаты принимают только два значения, то к ним применимы все операции булевой алгебры, например: отрицание, импликация, конъюнкция, дизъюнкция и т. д. Например, обозначим предикатом EQ(x, y) отношение равенства («x = y»), где x и y принадлежат множеству вещественных чисел. В этом случае предикат EQ будет принимать истинное значение для всех равных x и y. Более житейским примером может служить предикат ПРОЖИВАЕТ(x, y, z) для отношения «x проживает в городе y на улице z» или ЛЮБИТ(x, y) для «x любит y», где множество M — это множество всех людей.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 309; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.124.232 (0.008 с.) |

 ), если они являются логическим следствием друг друга, логически эквивалентные формулы имеют одинаковые значения при любой интерпретации.
), если они являются логическим следствием друг друга, логически эквивалентные формулы имеют одинаковые значения при любой интерпретации.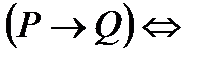

 Q
Q

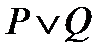




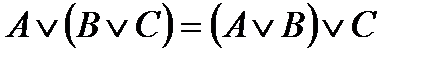

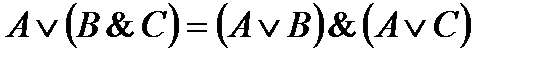

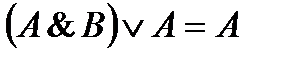
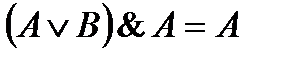
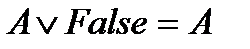



 B
B