
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Диаметр, радиус, центр графа.
Пусть G – конечный неориентированный граф. Тогда можно определить его диаметр d(G)=max d(v¢,v²). Кратчайшие простые цепи, связывающие вершины v¢,v²ÎG с максимальным расстоянием между ними, называются диаметральными простыми цепями. Пусть v – произвольная вершина рассматриваемого графа G. Максимальным удалением в графе G от вершины v называется величина r(v)=max d(v,v¢). Вершина v называется центром графа G, если максимальное удаление от нее принимает минимальное значение r(G)=min r(v¢). Максимальное удаление r(G) от центра называется радиусом графа, а любая кратчайшая цепь от центра v до максимально удаленной от него вершины v¢ - радиальной цепью. Центр не обязательно должен быть единственным. Например, в полном неориентированном графе K(V), в котором любые две различные вершины v¢,v²ÎV соединены ребром, радиус равен единице и любая вершина vÎV является центром. Произведение графов. Прямое произведение графов. Прямые произведения графов. Пусть даны графы G1и G2 с множествами вершин V1и V2. У прямого произведения этих графов F = G1×G2 множеством вершин является прямое произведение V = V1×V2. Ребра произведения могут быть определены различными способами. При одном из определений в произведении Fграфов G1и G2ребро Чаще всего используется третье определение, согласно которому ребро
Тогда матрица смежности прямого произведения графов G1и G2 при таком определении равна
Аналогично определяется прямое произведение любого множества графов.
Эйлеровы циклы. Цикл графа G, содержащий все его рёбра, наз. эйлеровым. Граф, имеющий эйлеров цикл наз. эйлеровым. Терорема. Для каждого связного графа G следующие условия эквивалентны: 1. G – эйлеров граф. 2. Каждая вершина графа G имеет чётную степень. 3. Мн-во рёбер графа можно разбить на простые циклы, т.е. U=Èki=1 ui (ui Çuj=Æ, (i¹j), ui=Æ). Доказательство. Пусть G – эйлеров граф. Покажем, что каждая вершина имеет чётную степень. Каждая вершина простого цикла имеет степень 2. Поэтому, если в графе G существует эйлеров цикл, то каждая вершина должна иметь чётную степень. Пусть каждая вершина имеет чётную степень. Выбираем произвольную вершину графа i1 и движемся от неё по ребру к смежной вершине i2, и т.д. каждый раз выбирая новое ребро. Т.к. граф связен, число рёбер в графе конечно и войдя в вершину по некоторому ребру мы можем выйти по другому, то через некоторое число шагов какая-то вершина ik повторится. Тогда i1,i2,…,ik,i1 образует простой цикл в исодном графе (u1). Удалим рёбра этого цикла из исходного графа. Новом графе каждая не изолированя вершина имеет чётную степень, поэтому процедуру выделения простых циклов можно применять к каждой компоненте связности, отличной от изолированой вершины. Через некоторое число шагов мы получим исх. разбиение. Пусть закдано разбиение U=Èki=1 ui. Покажем, что $ эйлеров цикл. Т.к. G – связный граф, то найдутся два простых цикла имеющих общую вершину эти два цикла можно объеденить (склеить) в один цикл. Пусть u’ и u’’ имеют общую вершину k. u’=(j1,j2,…,jl-1,k,j1+1,…,jm,j1), u’’=(t1,t2,…,td-1,k,td+1,…,tf,t1), u*=(j1,j2,…,jl-1,k,td-1,…,t1,tf,tf-1,…,td+1,k,j1+1,…,jm,j1). Число циклов при этом уменьшиться на еденицу. Повторяя процедуру склеивания, в итоге получим один цикл, содержащий все рёбра исходного графа – эйлеров цикл, ч.т.д. Док-во данной теоремы можно использовать в качестве алгоритма при построении эйлерового цикла, если он существует. Теорема Эйлера. Теорема: Граф называется Эйлоровым тогда и только тогда, когда он является связным и степени всех его вершин являются четными. Необходимость: В несвязанном графе каждый цикл принадлежит какой-либо его мвязанной части, т.е. не проходит через все его ребра (кроме случая, когда все компоненты связности графа, кроме одной, - изолированные вершины). Кроме того, каждый раз, когда эйлеров цикл приходит в какую-нибудь вершину, он должен выйти из нее по другому ребру, т.е. инцидентные вершинам ребра можно разбить на пары соседних в эйлеровом цикле. Исключением являются ребра, инцидентные началу эйлерова цикла, совпадающему с его концом. Сначала цикл выходит из этой вершины по какому-либо ребру. Затем он, возможно, несколько раз возвращается в эту вершину, каждый раз входя по новому ребру и выходя так же по новому, но другому ребру. В конце концов он возвращается в исходную вершину по не затронутому ранее ребру. Таким образом, и в этом случае инцидентные этой вершине ребра также распадаются на пары соседних в эйлеровом цикле, но одна из этих пар состоит из ребра, проходимого в начале процесса, и другого, замыкающего этот процесс.
Достаточность: Пусть G – конечный связный граф с четными степенями всех вершин. Начнем построение эйлерова цикла с поизвольной вершины v графа G. каждый раз, когда мы добавляем к маршруту новое ребро и приходим в новую вершину, число свободных ребер в этой вершине изменяется на единицу. Если до этого оно было четным, то теперь оно становится нечетным и не может оказаться нулем. После ухода из этой вершины число свободных инцидентных ей ребер уменьшается еще на 1 и вновь становиться четным. Исключением является свободная вершина, у которой после начала процесса число свободных ребер нечетно и остается нечетным после каждого возвращения в эту вершину и ухода из нее. Описанный ранее процесс построения цикла может закончиться лишь в той вершине, откуда он начинался, но при этом не обязательно, чтобы он проходил через все ребра графа. Принадлежащие ему ребра порождают связную часть P графа G, в которой степени всех вершин четны. Значит, они четны и для разности G\P. Так как граф G связен, в дополнении G\P существует хотя бы одна вершина v¢, принадлежащая также части Р. Начиная с этой вершины, можно провести, как и ранее, построение цикла Р¢ в G\P, кончающегося в вершине v¢. Эта вершина, кроме того, разбивает цикл Р на два участка Р1 с началом v и концом v¢ и Р2 с началом v¢ и концом v. Тогда Р1ÈР¢ÈР2 – также цикл, начинающийся в вершине v, но имеющий большее число ребер. Если и этот цикл не проходит через все ребра, этот процесс расширения цикла можно повторить. Каждый раз число ребер в цикле увеличивается не менее чем на два, значит, в конце концов эйлеров цикл будет построен.
Эйлеровы цепи. Так называется цепь, включающая все ребра данного конечного неориентированного графа G, но имеющая различные начало v¢ и конец v². Чтобы в графе существовала эйлерова цепь, необходимы его связность и четность всех вершин, кроме начальной v¢ и конечной v². Последние две вершины должны иметь нечетные степени: из v¢ мы лишний раз выходим, а в v² лишний раз входим. Эти условия достаточны для существования эйлеровой цепи. Можно искать наименьшее число не пересекающихся по ребрам цепей, покрывающих конечный связный граф G. Пусть G не является эйлеровы графом, k – число его вершин нечетной степени. Каждая вершина нечетной степени должна быть концом хотя бы одной из покрывающих цепей. Следовательно, число последних не меньше, чем k/2. Но ограничиться k/2 цепями не так трудно. Соединим вершины нечетной степени попарно k/2 ребрами произвольным образом. Тогда степень каждой их этих вершин увеличится на единицу и станет четной. Получится эйлеров граф, в котором существует эйлеров цикл. Выбросим теперь обратно присоединенные ребра. При выбрасывании первого ребра эйлеров цикл превратиться в эйлорову цепь, а при выбрасывании каждой следующей цепи одна из возникших к этому моменту цепей разобъется на 2 части. Таким образом, общее число этих цепей станет k/2. При построении никогда не выбрасываются соседние по эйлерову циклу ребра.
Гамильтоновы циклы.
На рис. изображены граф с гамильтоновым циклом (рис. а) и циклически связный граф, в котором нет гамильтонова цикла (рис. б). В последнем, чтобы пройти через вершины, расположенные внутри сторон треугольника АВС, гамильтонов цикл должен содержать все лежащие на этих сторонах ребра. Но тогда он не проходит через расположенную в центре треугольника вершину 0. Иногда можно построить проходящую через все вершины графа простую цепь с началом и концом в различных заданных вершинах V ', V"
|
|||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 823; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.218.215 (0.01 с.) |
 имеется тогда, когда в графе G1есть ребро
имеется тогда, когда в графе G1есть ребро  или в графе G2 —
или в графе G2 — 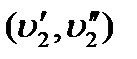 . В другом определении для этого требуется существование обоих этих ребер. В первом случае элементы матрицы смежности определяются формулой
. В другом определении для этого требуется существование обоих этих ребер. В первом случае элементы матрицы смежности определяются формулой 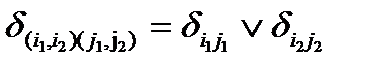 во втором
во втором 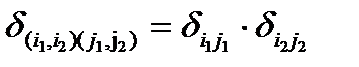 . Таким образом, в обоих случаях матрица смежности произведения является тензорным произведением матриц смежности сомножителей, но в первом случае произведение элементов матрицы понимается как логическая сумма
. Таким образом, в обоих случаях матрица смежности произведения является тензорным произведением матриц смежности сомножителей, но в первом случае произведение элементов матрицы понимается как логическая сумма  (или), а во втором -— как логическое (и обычное) произведение (и).
(или), а во втором -— как логическое (и обычное) произведение (и). , а в графе G2 есть ребро
, а в графе G2 есть ребро 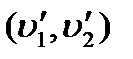 , а
, а 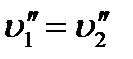 . Пусть
. Пусть 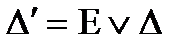 , где E — единичная матрица, а
, где E — единичная матрица, а  — матрица смежности рассматриваемого графа:
— матрица смежности рассматриваемого графа: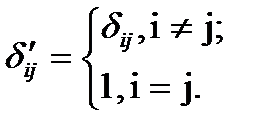

 , т.е.
, т.е.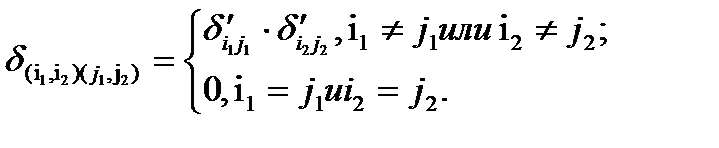
 Еще быстрее мы попадем к выходу из лабиринта (когда его граф G связен), двигаясь по гамильтонову циклу, т. е. по простому циклу, проходящему через все вершины рассматриваемого графа G. Однако не во всяком связном графе, содержащем циклы, существует га-мильтонов цикл. Более того, через любые две вершины рассматриваемого графа может проходить простой цикл (в этом случае граф G называется циклически связным), а га-мильтонов цикл при этом может отсутствовать.
Еще быстрее мы попадем к выходу из лабиринта (когда его граф G связен), двигаясь по гамильтонову циклу, т. е. по простому циклу, проходящему через все вершины рассматриваемого графа G. Однако не во всяком связном графе, содержащем циклы, существует га-мильтонов цикл. Более того, через любые две вершины рассматриваемого графа может проходить простой цикл (в этом случае граф G называется циклически связным), а га-мильтонов цикл при этом может отсутствовать. С. Такая цепь тоже называется гамильтоновой.
С. Такая цепь тоже называется гамильтоновой.


