
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функциональная полнота. Теорема Поста
Сис-ма ф-ий F назыв. функц.-полной, если любая логическая ф-ия может быть представлена формулой над мн-вом F, то есть явл. Суперпозицией ф-ии из F. Рассм. сис-му ф-ий, содержащих Для любой логической ф-ийй можна взять ее представление и все входящие в нее операции заменить формулами с Теорема Поста. Для того чтобы некоторый набор функций K был полным, необходимо и достаточно, чтобы в него входили функции, не принадлежащие каждому из классов T0, T1, L, M, S. Заметим, что необходимость этого утверждения очевидна, так как если бы все функции из набора К входили в один из перечисленных классов, то и все суперпозиции, а значит, и замыкание набора входило бы в этот класс и класс К не мог быть полным. Из этой теоремы следует довольно простой способ выяснения полноты некоторого набора функций. Для каждой из этих функций выясняется принадлежность к перечисленным выше классам. Результаты заносятся в так называемую таблицу Поста (в нашем примере эта таблица составлена для 4-х функций, причем знаком “+” отмечается принадлежность функции соответствующему классу, знак “–” означает, что функция в него не входит). В соответствии с теоремой Поста набор функций будет полным тогда и только тогда, когда в каждом столбце таблицы Поста имеется хотя бы один минус. Таким образом, из приведенной таблицы следует, что данные 4 функции образуют полный набор, но эти функции не являются базисом. Из этих функций можно образовать 2 базиса: f3, f1 и f3, f2. Полными наборами будут любые наборы содержащие, какой-либо базис. Непосредственно из таблицы Поста следует, что число базисных функций не может быть больше 5. Нетрудно доказать, что на самом деле это число меньше или равно 4. Блок-схемы алгоритмов Блок-схемы алгоритмов Среди универсальных форм представления или записи алгоритмов можно выделить так называемые блок-схемы алгоритмов. Универсальность этой формы обусловлена тем, что в ней заранее не определяются абстракции, которые могут специфицироваться в блоках даже с применением обычного разговорного языка. Блоки являются всего лишь шаблоном для описания действий в процессе решения задачи, а связи между блоками определяют последовательность этих действий.
Если операторный или условный блоки имеют более одного входа, то изо-бражение входов совмещается. На связях, определяющих последовательность выполнения блоков, стрелки не обязательны, если их направление соответствует продвижению “сверху-вниз” и “слева-направо”. Ограничения на геометрические размеры блоков в этом случае не вводятся.
Эта же форма описания алгоритмов принята для оформления программной документации. Набор блоков, используемый для документирования программ, значительно шире и стандартизован. 95.Машины Тьюринга. Основные определения. Машина Тьюринга (МТ) — математическая абстракция, представляющая вычислительную машину общего вида. Была предложена Аланом Тьюрингом в 1936 году для формализации понятия алгоритма. Машина Тьюринга представляет собой автомат, имеющий бесконечную в обе стороны ленту, счи- тывающую головку и управляющее устройство. Управляющее устройство может находиться в одном из состояний, образую- щих конечное множество Q = {q0, q1,..., qn}. Множество Q называют внутренним алфавитом машины Тьюринга. Принципиальное отличие машины Тьюринга от вычисли- тельных машин состоит в том, что ее запоминающее устройство представляет собой бесконечную ленту, из-за которой невозможна ее физическая реализация. Лента разделена на ячейки, в каждой из которых может быть записан один из символов конечного алфавита A = {a0, a1,..., am}, который называют входным алфавитом машины Тьюринга. Во время функционирования машины Тьюринга может быть заполнено конечное число ячеек. Считывающая головка в каждый момент времени обозревает ячейку ленты, в зависимости от символа в этой ячейке и состояния управляющего устройства записывает в ячейку новый символ или оставляет его без изменения, сдвигается на ячейку влево или вправо или остается на месте. При этом управляющее устройство переходит в новое состояние или остается в старом. Среди состояний управляющего устройства выделены начальное состояние q0 и заключительное состояние qz. Таким образом, за один такт работы машина Тьюринга может считать символ, записать вместо него новый или оставить его без изменения и сдвинуть головку на одну ячейку влево или вправо или оставить ее на месте. Машина Тьюринга является расширением модели конечного автомата и, согласно тезису Чёрча — Тьюринга, способна имитировать (при наличии соответствующей программы) любую машину, действие которой заключается в переходе от одного дискретного состояния к другому.В состав Машины Тьюринга входит бесконечная в обе стороны лента, разделённая на ячейки, и управляющее устройство с конечным числом состояний. Управляющее устройство может переме -щаться влево и вправо по ленте, читать и записывать в ячейки символы некоторого конечного алфавита. Выделяется особый пустой символ, заполняющий все клетки ленты, кроме тех из них (конечного числа), на которых записаны входные данные.В управляющем устройстве содержится таблица переходов, кото- рая представляет алгоритм, реализуемый данной Машиной Тьюринга. Каждое правило из таблицы предписывает машине, в зависимости от текущего состояния и наблюдаемого в текущей клетке символа, записать в эту клетку новый символ, перейти в новое состояние и переместиться на одну клетку влево или вправо. Некоторые состояния Машины Тьюринга могут быть помечены как терминальные, и переход в любое из них означает конец работы, остановку алгоритма.Машина Тьюринга называется детерминированной, если каждой комбинации состояния и ленточного символа в таблице соответствует не более одного правила, и недетерминированной в противном случае.
Машины Тьюринга.Сложение Приведем пример машины Тьюринга, выполняющей унарное сложение двух операндов. Операнды представляются в унар -ной системе, т. к. целое неотрицательное число n представляет ся n+1 единицей. Табличное представление МТ
Машины Тьюринга.Копирование Копирование
Машина Тьюринга представляет собой автомат, имеющий беско нечную в обе стороны ленту, считывающую головку и управ - ляющее устройство. Управляющее устройство может находи - ться в одном из состояний, образующих конечное множество Q = {q0, q1,..., qn}. Множество Q называют внутренним алфа - витом машины Тьюринга. Принципиальное отличие машины Тьюринга от вычислительных машин состоит в том, что ее запо- минающее устройство представляет собой бесконечную ленту, из-за которой невозможна ее физическая реализация. Лента разделена на ячейки, в каждой из которых может быть записан один из символов конечного алфавита A = {a0, a1,..., am}, который называют входным алфавитом машины Тьюринга. Во время функционирования машины Тьюринга может быть запол- нено конечное число ячеек. Считывающая головка в каждый момент времени обозревает ячейку ленты, в зависимости от символа в этой ячейке и состояния управляющего устройства записывает в ячейку новый символ или оставляет его без изме - нения, сдвигается на ячейку влево или вправо или остается на месте. При этом управляющее устройство переходит в новое состояние или остается в старом. Среди состояний управляю - щего устройства выделены начальное состояние q0 и заклю - чительное состояние qz. Таким образом, за один такт работы машина Тьюринга может считать символ, записать вместо него новый или оставить его без изменения и сдвинуть головку на одну ячейку влево или вправо или оставить ее на месте.
Типы вершин Рассмотрим дерево
Пусть вершина типа k есть вершина максимального типа. Из определения типа вершин дерева следует, что эксцентриситет единственной вершины максимального типа равен ее типу, то есть равен k, а эксцентриситет каждой из двух вершин максимального типа равен k-1. При этом эксцентриситет любой вершины не максимального типа будет обязательно больше.
|
||||||||||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 247; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.143.239 (0.009 с.) |
 .Эта сис-ма явл. функц. полной т.к. на основании теоремы любую ф-ию булевой алгебры можна представить, используя конъюнкцию, дизъюнкцию, отрицание. Функц.-полная - сис-ма ф-ий, ф-ии которой можна выразить
.Эта сис-ма явл. функц. полной т.к. на основании теоремы любую ф-ию булевой алгебры можна представить, используя конъюнкцию, дизъюнкцию, отрицание. Функц.-полная - сис-ма ф-ий, ф-ии которой можна выразить 


 Примеры выполнения МТ «1» + «1»
Примеры выполнения МТ «1» + «1»
 -го слова. Обозначение
-го слова. Обозначение 



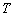 с
с  вершинами. Назовем его концевые вершины вершинами типа 1. Теперь удалим все вершины типа 1 и концевые ребра. В результате получим связный граф без циклов
вершинами. Назовем его концевые вершины вершинами типа 1. Теперь удалим все вершины типа 1 и концевые ребра. В результате получим связный граф без циклов  , то есть опять дерево, но с уже меньшим количеством вершин. Концевые вершины дерева
, то есть опять дерево, но с уже меньшим количеством вершин. Концевые вершины дерева 



