
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение уравнения Шредингера для простейшихСодержание книги
Поиск на нашем сайте
Модельных систем Частица в одномерной потенциальной яме. Частица свободно движется вдоль оси х в интервале от 0 до L и вне этого интервала находиться не может.
Обозначим
Требование Ψ (L) = 0 выполняется при kl = πn (n = 1, 2, 3 …)
Туннельный эффект
Схема туннельного эффекта. . Частица на окружности
Решения либо cos l φ, либо sin l φ, либо комбинация cos l φ+sin l φ
Ψ (φ) = Ψ (φ ± 2π) = Ψ (φ ± 4 π) =... l - целые числа (положительные или отрицательные) или ноль: l = 0,±1,±2,±3,....
где т - масса частицы
Решение уравнения Шредингера для атома водорода.
Сферическая полярная система координат
Ψ = Ψ (r, θ, φ)
Квантовое число l ограничено значениями 0, 1, 2, … (n - 1).
Параметр m является аналогом магнитного квантового числа в модели Бора – Зоммерфельда.
Квантовое число m может принимать значения 0, ±1, ±2, ±3, … ± l. Полный магнитный момент атома j определяется выражением
где k = ±1/2 (В. Паули) Спин - чисто квантовое свойство, недоступное объяснению с позиций классической физики. Эта точка зрения сохранилась до настоящего времени и широко представлена в литературе.
Спиновые квантовые числа некоторых элементарных Частиц и атомных ядер.
Физический смысл квантовых чисел электрона Орбиталью называют область пространства, соответствующую определенному набору квантовых чисел п, l и m, где вероятность нахождения электрона | Ψ |2 составляет 0,9 (90%) или функцию квантовых чисел п, l и m введенную для характеристики электронов без учета их спина.
Главное квантовое число п для реально существующих атомов имеет значения от 1 до 7, которые определяют: 1. Размеры орбитали. Энергию электронов, находящихся на орбитали. Буквенные обозначения главного квантового числа
Орбитальное (азимутальное) квантовое число l определяет момент импульса электрона и форму орбиталей.Зависит от n и принимает целочисленные значения от 0 до (n -1). Буквенные обозначения орбитального квантового числа
Магнитное квантовое число ml определяет ориентацию орбитали в пространстве, которая не может быть произвольной. Может принимать целочисленные значения от – l до + l, включая нуль. Спиновое квантовое число s определяет направление и величину проекции собственного магнитного момента электрона S на выбранную ось z в единицах постоянной Планка:
Двум противоположным направлениям проекций соответствуют значения s +1/2 и -1/2.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 194; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.184.184 (0.009 с.) |








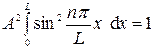





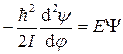









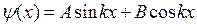
 при m = 0, ±1, ±2,…
при m = 0, ±1, ±2,…






