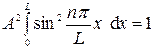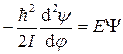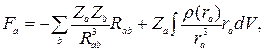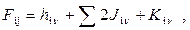Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Результаты квантово-химических исследований необходимо подтверждать ключевыми экспериментами.Содержание книги
Поиск на нашем сайте
НАЧАЛА КВАНТОВОЙ ХИМИИ И СТРОЕНИЕ МОЛЕКУЛ
«Все должно быть изложено так просто, как только возможно, но не проще». А. Эйнштейн.
Квантовая химия – раздел теоретической химии, в котором строение, свойства и взаимодействия веществ исследуются на основе представлений квантовой механики и экспериментально установленных закономерностей. Решаемые задачи: - изучение биологических и биологически активных веществ, исследование структуры высокоперспективных материалов, например высокотемпературных сверхпроводников, углеродных нанотрубок, фуллеренов; - изучение супрамолекулярных систем - сложных образований, являющихся результатом ассоциации нескольких химических частиц, связанных вместе межмолекулярными взаимодействиями. - исследование комплексных соединений, динамических свойств атомов и ионов в различных кристаллических и молекулярных структурах, и др. Результаты квантово-химических исследований необходимо подтверждать ключевыми экспериментами.
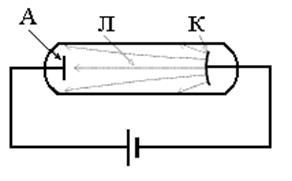
Тетраэдран Нобелевскими премиями были награждены: Л. Полинг за теорию гибридизации Р. Хоффманн и К. Фукуи за развитие квантово-химической теории механизмов реакций Р. Керл, Х. Крото и Р. Смолли за обнаружение по УФ спектрам межзвездного газа нанотрубок и последующий их синтез А.А. Бочвар и Е.Г. Гальперн теоретически предсказали фуллерены и рассчитали их электронную структуру М.Ю. Корнилов предсказал нанотрубки, которые позднее были открыты. Открытие сложного строения атома М. Фарадей установил, что электрические заряды, как и материя, имеют дискретный характер и существует некий минимальный заряд. Эксперименты с газоразрядными трубками показали, что в состав атомов должны входить отрицательно заряженные частицы, которые впоследствии были названы электронами. Схема опыта У. Крукса
A - анод, K - катод, Л - катодный луч Модель Томсона (1904 г.)
Положительный заряд равномерно распределен по всему объему атома. Отрицательньно заряженные электроны, образуя правильные конфигурации, закономерно вкраплены в эту положительную сферу. Их суммарный заряд равен положительному заряду сферы. Число и расположение электронов зависит от природы атома. Электроны находятся в равновесных положениях и при возбуждении могут колебаться около них, излучая в пространство электромагнитные волны.
Взаимное расположение электронов в атоме
Х. Гейгер и Е. Марсден (1906-1909 г.)
Квантовые и волновые свойства электромагнитного Излучения Опыт Юнга (1800 г.)
а б
в г
Корпускулярная модель
Схема возникновение интерференции между волнами х1 и х2, х 3 - результирующая волна.
Модели света Теория фотоэффекта
Строение атома по Бору Рассмотрваемые вопросы: интерпретация атомных спектров, положение о спектральных термах, комбинационный принцип, постулаты Бора, модель атома Бора, модель атома Зоммерфельда, эффект Зеемана, существование эллиптических орбит, квантовые числа электрона: главное, побочное, магнитное. Закономерности. «Спектры делают видимым многое не только на громадных мирах, таких как звезды, но и в безгранично мелких мирах, таких как частицы, и разработка в этой области обещает многое выяснить в области атомов и частиц». Д.И. Менделеев, 1903г.
Серия Брэккета (1922 г.)
И серия Пфунда (1924 г.)
Расположение линий в спектральных сериях определяется разностью двух величин (спектральных термов) Т, одна из которых зависит только от номера серии и постоянна для всех линий данной серии, а вторая зависит от номера линии в этой серии:
В. Ритц (1908 г.) - комбинационный принцип: волновые числа спектральных линий можно представить в виде разности характерных для атомов данного элемента величин – термов. Следствие: если в спектре наблюдаются линии с заданными частотами, то могут наблюдаться и линии, соответствующие суммам и разностям этих частот. Всю систему термов для атома водорода можно получить из равенства:
Н. Бор назвал значения чисел п в этом уравнении «квантовыми числами» (порядковыми номерами энергетических уровней). I. Атомная система устойчива только для определенной совокупности состояний - «стационарных состояний», которая в общем случае соответствует дискретной последовательности значений энергии атома. Каждое изменение этой энергии связано с полным «переходом» атома из одного стационарного состояния в другое.
II. Способность атома поглощать и испускать излучение подчиняется закону, по которому излучение, связанное с переходом, должно быть монохроматическим и иметь частоту ν, определяемую соотношением
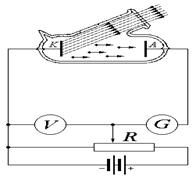
где h – постоянная Планка и Е 1и Е 2– энергия двух соответствующих стационарных состояний. Д. Франк и Г. Герц (1913 – 1914 гг.). При неупругих столкновениях электрона с атомом происходит передача энергии от электрона атому. Если внутренняя энергия атома изменяется непрерывно, то атому может быть передана любая порция энергии. Если же состояния атома дискретны, то при неупругом столкновении электрон может передать атому лишь определенные порции энергии.
Схема опыта Франка и Герца
Зависимость силы анодного тока в цепи от ускоряющей разности потенциалов eVа. Разница внутренних энергий основного состояния атома ртути и ближайшего возбужденного состояния eV равна 4,9 эВ, что доказывает дискретность внутренней энергии атома и, следовательно, справедливость первого постулата Бора. Где
Бегущие волны.
φ – амплитуда смещения расстоянии х от начала струны; λ – длина волны; ν — частота; а – постоянная (максимальное значение амплитуды); с – скорость распространения волны a 1 φ 1 + a 2 φ 2
где λ = c/v
УравнениеШредингера
1. Уравнение Шредингера описывает состояние микросистем (атомов, молекул, ионов и др.) с учетом корпускулярно-волнового дуализма. 2. Уравнение – постулат, но отражает объективную реальность. Это закон природы. Решения, полученные на его основании (значения Е для заданных х, у, z), не противоречат экспериментальным фактам. 3. Уравнение связывает энергию системы (электрона) с ее волновым движением. Энергия электрона зависит только от некоторой волновой функции Ψ, которая характеризует его движение. Поскольку волновая функция полностью определяет состояние системы, любому набору координат частиц системы при заданном значении t соответствует только одно значение Ψ. 4. Решение уравнения Шредингера позволяет найти вид Ψ – функций, характеризующих возможные состояния микрочастиц в данных условиях, и соответствующие им значения энергии. Полученные данные позволяют составить некий образ системы (атома).
Вероятность пребывания электрона в данной единице объема атома dV равна Ψ2dV иназывается электронной плотностью. Вероятность найти частицу в любом элементе объема не должна обращаться в бесконечность.
Модельных систем Частица в одномерной потенциальной яме. Частица свободно движется вдоль оси х в интервале от 0 до L и вне этого интервала находиться не может.
Обозначим
Требование Ψ (L) = 0 выполняется при kl = πn (n = 1, 2, 3 …)
Туннельный эффект
Схема туннельного эффекта.
. Частица на окружности
Решения либо cos l φ, либо sin l φ, либо комбинация cos l φ+sin l φ
Ψ (φ) = Ψ (φ ± 2π) = Ψ (φ ± 4 π) =... l - целые числа (положительные или отрицательные) или ноль: l = 0,±1,±2,±3,....
где т - масса частицы
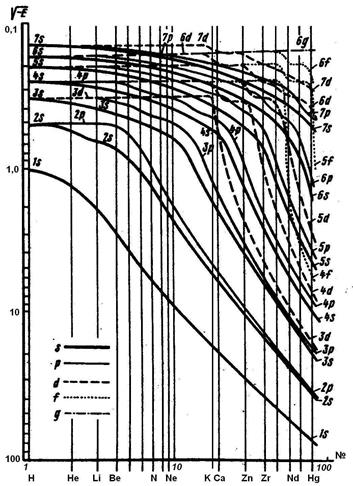
Частиц и атомных ядер.
Электронов в атоме натрия
Номера элемента.
Принцип Паули - в данном атоме или молекуле не может быть электронов, у которых бы все четыре квантовых числа совпадали; любая электронная, волновая функция должна, быть антисимметрична по отношению к перестановке любой пары электронов. Правило Хунда - в пределах одного подуровня электроны распределяются по орбиталям таким образом, чтобы модуль суммы их спиновых квантовых чисел был максимальным . Принцип минимума энергии - наиболее устойчивыми состояниями любой системы являются состояния с минимальным запасом энергии. Энергия подуровней растет в ряду: 1 s < 2 s < 2 р < 3 s < 3 р < 4 s < 3 d < 4 р < 5 s < 4 d < 6 p < 6 s < 4 f ≈ 5 d< 6 p<7 s <5f ≈ 6d < 7p... 1-е правило Клечковского − уровни и подуровни атомов заполняются электронами в порядке возрастания суммы главного и орбитального квантовых чисел (n + l). 2-е правило Клечковского − при одном и том же значении суммы (n + l) заполнение подуровней происходит в порядке возрастания главного квантового числа п.
Электронная конфигурация (формула) атома − это условная запись распределения электронов по орбиталям в основном состоянии этого атома. [Ne] ≡ 1 s 22 s 22 p 6; [Cl] ≡ 1 s 22 s 22 p 63 s 23 p 5 или [Ne] 3 s 23 p 5 1 s 2 2 s 22 px 2 py Хром [Ar]3 d 54 s 1, медь [Ar]3 d 104 s 1, палладий [Kr]4 d 105 s 1, ниобий [Kr]4 d 45 s 1, рутений [Kr]4 d 75 s 1, родий [Kr]4 d 85 s 1, платина [Xe]4 f 145 d 85 s 1
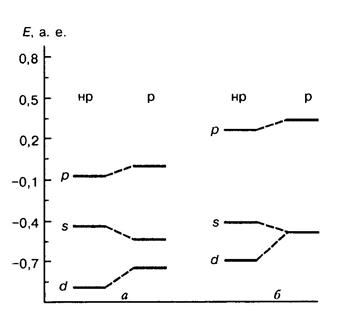
Энергетические уровни, в рассчитанные в релятивистском (р) и нерелятивистском (нр) приближениях: И СТРОЕНИЯ МОЛЕКУЛ Метод валентных связей
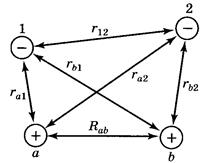
Fa − вектор силы, действующей на ядро с номером а; Zа − заряд ядра с номером а; ρ (ra) - электронная плотность в окрестности точки с радиус-вектором ra, проведенным от ядра а в данную точку; Rab − расстояние между ядрами a и b;ra − расстояние от ядра а до элемента объема, содержащего электронный заряд ρ (ra) dV
где х1, y1 и z1 − координаты первого электрона; х2, у2, z2 — координаты второго электрона
Основные принципы метода 1. Одинарная ковалентная химическая связь между двумя атомами образуется обобществленной электронной парой. Электронная пара − два электрона, имеющие общую волновую функцию и отличающиеся значениями спинового квантового числа. 2. Связывающая электронная пара образуется при обобществлении, «перекрывании» орбиталей двух взаимодействующих атомов. Перекрываться могут только орбитали валентных электронных уровней имеющие одинаковую симметрию относительно межъядерной оси. Перекрывание атомных орбиталей приводит к образованию связи только при совпадении знаков волновых функций для перекрывающихся частей орбиталей. 3. Уменьшение энергии системы при образовании ковалентной химической связи вызвано действием сил электрической природы: остовы взаимодействующих атомов притягиваются к зоне повышенной электронной плотности, которая возникает в пространстве между ядрами при перекрывании электронных орбиталей. Чем больше перекрываются орбитали, тем прочнее связь и тем она короче. Гибридизация атомных орбиталей - взаимодействие разных по типу и близких по энергии атомных орбиталей данного атома с образованием набора новых орбиталей одинаковой формы и энергии. Ферроцен Метод молекулярных орбиталей (ММО) Молекула рассматривается как единая система ядер, находящихся в равновесных положениях, и электронов. Основные положения: 1. При решении уравнения Шредингера получают допустимые волновые функции, описывающие энергетические уровни молекул – молекулярные орбитали (МО) 2. При образовании химической связи МО возникают из атомных орбиталей (АО). Центрами МО являются ядра атомов молекулы. 3. Молекулярным орбиталям соответствуют молекулярные квантовые числа. 4. Молекулярные волновые функции (МВФ) имеют тот же физический смысл, что и атомные, величина | Ψ | 2dV пропорциональна вероятности обнаружения электрона в данном элементе объема dV. Многоатомные молекулы
Образование трехцентровых молекулярных орбиталей
Образование полосы N орбиталей при последовательном Добавлении атомов в линию.
В которых
где: h iν – остовные интегралы, описывающие энергию электрона в поле атомных ядер; J iν – двухэлектронные кулоновские интегралы, описывающие энергию электростатического отталкивания электронов, находящихся на орбиталях Ψ μ и Ψ ν; K iν – обменный интеграл, описывающий понижение энергии взаимодействия электронов с параллельными спинами и расположенных на разных орбиталях; S μn – интеграл перекрывания между атомными орбиталями μ и n показывающий степень их пространственного перекрывания.
где a 0 - боровский радиус (0,0529нм ), Z – эффективный заряд ядра (для атома углерода Z=3,25), R – межатомное расстояние, Å. В табл. 1.10 показано изменение величины S CC в зависимости от расстояния С─С. Изменение значений SCC в зависимости от межатомного расстояния С─С
Типы учитываемых АО:
Водородоподобные. Слетеровские функции (STO). Гауссовские функции (GTO).
Свойств молекул
Полуэмпирические методы. Число кулоновскихинтеграллов для молекуле пропана, возникающих в различных методах расчета.
Координационных соединений. Спектрохимический ряд I– < Вr– < Cl– ≈ S CN– < F– < ОН– < Н2О < N CS– < CN– < NH3 < <H2NC2H4NH2 < NO2– < C N–
Теория поля лигандов [ML6In+, где М – d -элемент 3-го периода.
Диаграмма уровней МО октаэдрического комплекса [ ML6 I n+, где L – σ-донорные лиганды.
Диаграмма уровней МО октаэдрического комплекса [ML6]n+ с учетом возможных π-взаимодействий металл – лиганд НАЧАЛА КВАНТОВОЙ ХИМИИ И СТРОЕНИЕ МОЛЕКУЛ
«Все должно быть изложено так просто, как только возможно, но не проще». А. Эйнштейн.
Квантовая химия – раздел теоретической химии, в котором строение, свойства и взаимодействия веществ исследуются на основе представлений квантовой механики и экспериментально установленных закономерностей. Решаемые задачи: - изучение биологических и биологически активных веществ, исследование структуры высокоперспективных материалов, например высокотемпературных сверхпроводников, углеродных нанотрубок, фуллеренов; - изучение супрамолекулярных систем - сложных образований, являющихся результатом ассоциации нескольких химических частиц, связанных вместе межмолекулярными взаимодействиями. - исследование комплексных соединений, динамических свойств атомов и ионов в различных кристаллических и молекулярных структурах, и др. Результаты квантово-химических исследований необходимо подтверждать ключевыми экспериментами.
Тетраэдран
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 191; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.49.162 (0.014 с.) |








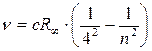 n = 5, 6, 7…
n = 5, 6, 7…
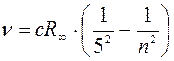 n = 6, 7, 8…
n = 6, 7, 8…
 = Tn - Tk
= Tn - Tk
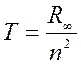 (n =1, 2,…)
(n =1, 2,…)




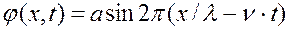
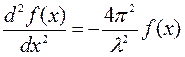 ,
,
 а
а
 б
б