
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнения, допускающие понижение порядка.
Уравнения вида F(x, y(k), y(k + 1), …, y(n)) = 0, не содержащие искомой функции. Порядок такого уравнения можно понизить на k единиц, взяв за новую неизвестную функцию низшую из производных z = y(k). Исходное уравнение примет вид F(x, z, z`, …, z(n – k)) = 0. Пример: xy`` = y`ln(y`/x). Полагая y` = z(y`` = z`) приведем уравнение к виду xz` = zln(z/x). Это однородное уравнение первого порядка. Полагая z/x = t(z = xt), z` = t + xt`, получим t`x + t = tlnt и, разделяя переменные,
Дифференциальные уравнения вида F(y, y`, y``, …, y(n)) = 0, не содержащие независимой переменной. Порядок уравнения понижаем положив y` = z, а за новый аргумент приняв у. В этом случае y``, y```, … можно, по правилу дифференцирования сложной функции, выразить через z и производные от z по у ( Пример: 1 + (y`)2 = yy``. Полагая
Линейные дифференциальные уравнения второго порядка. Линейным дифференциальным уравнением n порядка называется уравнение вида y(n) + a1(x)y(n–1) + … + an–1(x)y` + an(x)y = f(x) где функции a1(x), a2(x), … и f(x) заданы и непрерывны в некотором интервале (a, b). Уравнение называется линейным неоднородным при f(x) ¹ 0 и линейным однородным при f(x) = 0. Однородное уравнение с той же левой частью, что и данное неоднородное, называется соответствующим ему. Рассмотрим некоторые свойства линейных уравнений на примере уравнений второго порядка y`` + a1(x)y` + a2(x)y = f(x) (9.6).
Однородные уравнения Важное свойство уравнений вида y`` + a1(x)y` + a2(x)y = 0 (9.6`), определяется теоремой о структуре общего решения: если у1 и у2 два линейно независимых решения уравнения (9.6`), то у = С1у1 + С2у2 (9.7), где С1 и С2 – произвольные постоянные, есть его общее решение. Две функции у1 и у2 называются линейно независимыми на отрезке [a, b], если a1у1 + a2у2 ¹ 0 ни при каких a1 и a2, не равных нулю одновременно, ни в одной точке отрезка [a, b]. Определитель вида
Неоднородные уравнения. Структура общего решения линейного неоднородного уравнения (9.6) определяется следующим образом: Общее решение неоднородного уравнения (9.6) равно сумме любого его частного решения и общего решения соответствующего однородного уравнения (9.6`). Оставляя пока открытым вопрос о способах отыскания общего решения однородного уравнения, рассмотрим один из методов отыскания частного решения линейного неоднородного уравнения – метод вариации произвольных постоянных (метод Лагранжа). Заключается он в следующем. Пусть известно общее решение уравнения (9.6`), соответствующего уравнению (9.6):
`у = С1у1 + С2у2 (9.7).
Будем искать частное решение уравнения (9.6) в виде у* = С1(х)у1 + С2(х)у2, где С1(х) и С2(х) функции подлежащие определению. Продифференцируем последнее равенство: у*` = С`1у1 + С1у1` + С`2у2 + С2у`2 и наложим на искомые функции С1 и С2 дополнительное условие: С`1у1 + С`2у2 = 0 (1). Первая производная у*` примет вид у*` = С1у1` + С2у2`. Дифференцируя это выражение, получим: у*``= С`1у1` + С1у1`` + С`2у2` + С2у2``. Подставим у*, у*`, у*`` в (9.6) (напомним, что любое решение дифференциального уравнения, будучи подставлено в уравнение, обращает его в тождество).
C1y1`` + С2y2``+ С1y1` + C2y2` + a1(С1y1` + C2y2`) + a2(C1y1 + C2y2) = f(x) или
C1(y1`` + а1y1` + a2y1) + С2(y2`` + a1y2` + a2y2) + C1`y1` + C2`y2` = f(x). Выражения, стоящие в скобках, обращаются в нуль, так как у1 и у2 – решения однородного уравнения и последнее равенство примет вид C1`y1` + C2`y2` = f(x) (2). Функция (9.7) будет решением неоднородного уравнения (9.6) в случае, если функции С1 и С2 удовлетворяют системе уравнений (1) и (2). Определитель системы – это определитель Вронского для линейно независимых функций у1 и у2 и, следовательно, не равен нулю. Решая систему, найдем С1 и С2 как определенные функции от х: С1 = j1(х) и С2 = j2(х). Интегрируя, получим где ` С1 и ` С2 – произвольные постоянные. Подставляя полученные выражения в (9.7) получим общий интеграл уравнения (9.6) у =`у + у*.
Пример:
С1`x2 + C2` = 0 и 2С1`x = x, откуда
Общее решение: Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами – это уравнения вида (9.6), в которых коэффициенты а1 и а2 представляют собой постоянные величины. Рассмотрим решение однородных уравнений (9.6`). Будем искать линейно независимые частные решения у1 и у2 в (9.7) в виде у = еkх, где k – const (Метод был предложен Л. Эйлером). Тогда у` = kеkх и у`` = k2еkх. Подставляя решение в (9.6`) получим еkх(k2 + а1k + а2) = 0 и т.к. еkх ¹ 0, k2 + а1k + а2 = 0 (9.8). Уравнение (9.8) называется характеристическим уравнением по отношению к уравнению (9.6`). Корни уравнения (9.8) определяются по известной формуле для корней квадратного уравнения и при этом возможны следующие случаи: 1. Корни действительны и различны (k1 ¹ k2), частные решения Пример: y`` + y` – 2y = 0. Характеристическое уравнение k2 + k – 2 = 0; k1 = 1 и k2 = –2 и общее решение 2. Корни характеристического уравнения равны, k1 = k2 = k. В этом случае частные решения у1 и у2 целесообразно искать в виде 3. Корни характеристического уравнения комплексные. Известно, что, в общем случае, дискриминант квадратного уравнения может быть отрицательным и тогда уравнение не имеет действительных корней. Пример: у2 – 2у + 5 = 0; Выражение вида z = a + i b, где a и b – действительные числа, а i – мнимая единица, определяемая равенством i 2 = –1, называется комплексным числом a называется действительной, а b – мнимой частью комплексного числа. (Иногда используют обозначения: a = Rez и b = Imz; иногда мнимой частью называют произведение i b – это более естественно, но менее удобно). Два комплексных числа, отличающихся только знаком мнимой части, называются сопряженными. (Иногда для обозначения комплексно сопряженного числа используют символ z*, т.е. если z = a + i b, то z* = a – i b). Два комплексных числа z1 и z2 равны тогда и только тогда, когда равны их действительные (a1= a2) и мнимые (b1 = b2) части.
число z = a + i b. Если a= 0, то число 0 + i b = i b называется чисто мнимым (или просто мнимым) (ему соответствует точка на мнимой оси Оb), если b = 0, то число a + i 0=a оказывается действительным (вещественным) числом (ему соответствует точка на действительной оси Оa). Таким образом и действительные и мнимые числа суть частные случаи комплексного числа. На комплексной плоскости можно ввести и полярную систему координат (см.рис 9.1). Полярные координаты точки М: Примеры: 1) z = i; |z| = 1; arg z = p/2 2) z = 1; |z| = 1; arg z = 0 3) z = 1 + i; |z| =
При сложении комплексных чисел складываются их действительные и мнимые части, т.е. z 1 + z2 = (a1 + i b1) + (a2 + i b2) = (a1 + a2) + i (b1 + b2).
Произведение комплексных чисел можно найти в алгебраической z1 z2 = (a1 + i b1) (a2 + i b2) = (a1a2 – b1b2) + i (a1b2 + a2b1) и тригонометрической формах z1 z2 = r1(cosj1 + i sinj1) r2(cosj2 + i sinj2) = r1r2[cos (j1 + j2) + i sin (j1 + j2)] т.е. |z1 z2| = |z1| |z2|, arg (z1 z2) = arg z1 + arg z2.
Соответственно, при делении
Удобнее выполнять операции над комплексными числами в тригонометрической форме. Во многих случаях удобно использовать формулу zn = rn(cosj + i sinj)n = rn(cosnj + i sinnj); частный случай ее при r = 1: (cosj + i sinj)n = cosnj + i sinnj называют формулой Муавра. Важной в практическом отношении и показывающей одновременно связь тригонометрических и показательной функции является формула Эйлера e± i b = cosb ± i sinb. С её помощью вводится показательная форма комплексного числа: z = a + i b = r(cosj + i sinj) = re i j Вернемся к характеристическому уравнению однородного линейного уравнения второго порядка (9.6`). Если дискриминант квадратного уравнения отрицателен, оно имеет два комплексно сопряженных корня a + i b и a – i b. В этом случае частные решения однородного линейного уравнения второго порядка с постоянными коэффициентами примут вид у1 = е(a + i b)х и у2 = е(a + i b)х, или у1,2 = еaх cosbх ± i еaх sinbх, где у1 и у2 комплексные функции действительного аргумента, удовлетворяющие уравнению (9.6`). Если комплексная функция действительного аргумента у = u(x) + i v(x) удовлетворяет уравнению (9.6`), то ему удовлетворяют и функции u(x) и v(x). Соответственно, частными решениями в нашем случае будут действительные функции у1 = еaх cosbх и у2 = еaх sinbх. (у1 и у2 линейно независимы:
|
|||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 154; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.121.214 (0.028 с.) |
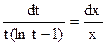 . Интегрируя, находим ln|lnt – 1| = ln|x| + lnC1, lnt – 1 = C1x и
. Интегрируя, находим ln|lnt – 1| = ln|x| + lnC1, lnt – 1 = C1x и 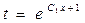 . Возвращаясь к исходной переменной приходим к уравнению первого порядка
. Возвращаясь к исходной переменной приходим к уравнению первого порядка 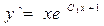 , решая которое найдем
, решая которое найдем 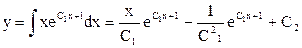 .
.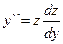 , и т.д.). Порядок уравнения понижается на единицу.
, и т.д.). Порядок уравнения понижается на единицу.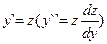 получим
получим 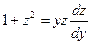 ; разделяя переменные и интегрируя:
; разделяя переменные и интегрируя: 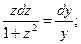
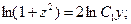
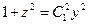
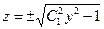 . Возвращаясь к старой переменной
. Возвращаясь к старой переменной 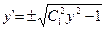 , откуда
, откуда 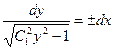 , и интегрируя, получим
, и интегрируя, получим 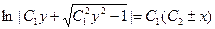 .
.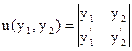 называется определителем Вронского (вронскианом) функций у1 и у2. Если у1 и у2 – частные решения уравнения (9.6`), то условие u(y1, y2) ¹ 0 является необходимым и достаточным условием линейной независимости этих решений. (Это условие можно записать и так:
называется определителем Вронского (вронскианом) функций у1 и у2. Если у1 и у2 – частные решения уравнения (9.6`), то условие u(y1, y2) ¹ 0 является необходимым и достаточным условием линейной независимости этих решений. (Это условие можно записать и так: 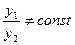 на отрезке [a, b]).
на отрезке [a, b]).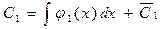 и
и 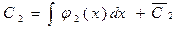 ,
,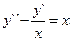 . Найдем общее решение соответствующего однородного уравнения
. Найдем общее решение соответствующего однородного уравнения 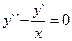 . Обозначив y` = z(y``= z`) получим
. Обозначив y` = z(y``= z`) получим 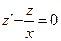 откуда z = y` = xC и `у = С1х2 + С2. Искомые функции С1(х) и С2(х) в общем решении и сходного уравнения определим из решения системы:
откуда z = y` = xC и `у = С1х2 + С2. Искомые функции С1(х) и С2(х) в общем решении и сходного уравнения определим из решения системы: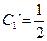 ,
, 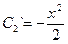 и
и 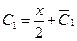 ,
, 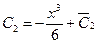 .
.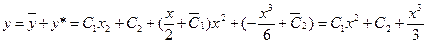 .
.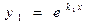 и
и 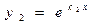 линейно независимы
линейно независимы 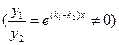 и общее решение принимает вид
и общее решение принимает вид 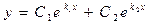 .
.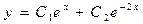 .
.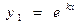 и
и 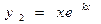 ; они линейно независимы: (
; они линейно независимы: (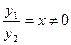 ) и общее решение примет вид
) и общее решение примет вид 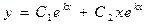 .
.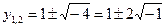 ; обозначив
; обозначив  , получим у1,2 = 1 ± 2 i.
, получим у1,2 = 1 ± 2 i.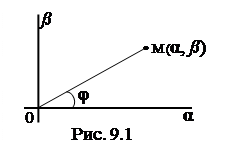 Комплексные числа изображаются точками на плоскости, называемой комплексной плоскостью. Поясним рисунком 9.1. На этой плоскости вводится система ортогональных координат: действительная (вещественная) ось Оa и мнимая ось Оb. Произвольной точке М(a;b) плоскости соответствует комплексное
Комплексные числа изображаются точками на плоскости, называемой комплексной плоскостью. Поясним рисунком 9.1. На этой плоскости вводится система ортогональных координат: действительная (вещественная) ось Оa и мнимая ось Оb. Произвольной точке М(a;b) плоскости соответствует комплексное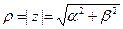 и
и 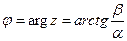 называются модулем и аргументом комплексного числа z. С учетом связи декартовых и полярных координат (a = r cos j, b = r sin j) получим тригонометрическую форму комплексного числа: z = r (cos j + i sin j).
называются модулем и аргументом комплексного числа z. С учетом связи декартовых и полярных координат (a = r cos j, b = r sin j) получим тригонометрическую форму комплексного числа: z = r (cos j + i sin j).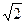 ; arg z = p/4 4) z = 1 – i; |z| =
; arg z = p/4 4) z = 1 – i; |z| = 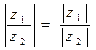 и
и 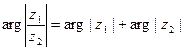 .
. ) и общее решение примет вид у = еaх (С1cosbх + С2sinbх).
) и общее решение примет вид у = еaх (С1cosbх + С2sinbх).


