
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Системы дифференциальных уравнений.
Система дифференциальных уравнений вида
называется нормальной системой.
Пример:
Умножим (1) на 2, (2) на 3 и сложив получим вторую интегрируемую комбинацию: Из системы уравнений (3) и (4) находим общее решение исходной системы: Некоторые нормальные системы дифференциальных уравнений удаётся свести к одному уравнению n- ого порядка, содержащему одну неизвестную функцию. Сделать это можно дифференцируя одно из уравнений системы и исключая все неизвестные кроме одной. Этот метод называют методом исключений Пример: Тесты 4.1. Обыкновенным дифференциальным уравнением является: 1) 2) 4.2. Какая из функций – общее решение уравнения 1) 2) 4.3. Для какого из уравнений справедлива теорема существования единственности решения? 1) 4.4. Решение уравнения 4.5. Какое из уравнений с разделяющимися переменными? 1) 4.6. Дано уравнение 1) 2) 4.7. Какое из уравнений линейное неоднородное первого порядка? 1) 4.8. Дано уравнение 1) 4.9. Какое из уравнений допускет понижение порядка? 1) 4.10. Дано уравнение 1) 4.11. Дано уравнение 1) 2) 4.12. Дано уравнение 1) Линейное однородное; 3) Нелинейное однородное; 2) Линейное неоднородное; 4) Нелинейное неоднородное. 4.13. Известны два частных решения уравнения второго порядка: 1) Да; 2) Нет. 4.14. Дано уравнение 1)
4.15. Какая из функций является функцией специального вида? 1) 4.16. Дано уравнение 1) 4.17. Преобразуя систему из двух линейных дифференциальных уравнений получили выражения: 1)
Ряды.
Числовые ряды.
Пусть u1, u2, …, un,... – бесконечная числовая последовательность, заданная формулой общего члена un = f(x), где n – номер члена. Выражение u1 + u2 + …+ un +... (10.1) называется числовым рядом, а числа u1, u2, …, un,... – членами ряда. Ряд удобно записывать в виде Сумму первых n членов обозначают через Sn и называют n –ой частичной суммой ряда: Sn = u1 + u2 + …+ un. Ряд называют сходящимся, если его n –ная частичная сумма Sn при неограниченном возрастании n стремится к конечному пределу, т.е. если Ряд a1 + a1q + a1q2 + … + a1qn–1+ …; где |q| < 1 (10.2), составленный из членов убывающей геометрической прогрессии, является сходящимся и имеет сумму
Приведём основные теоремы о сходящихся рядах.
1. Если сходится ряд (10.1), то сходится и ряд um + 1 + um + 2 + … (10.4) получаемый из данного ряда отбрасыванием первых m членов, т.е. на сходимость ряда не влияет отбрасывание конечного числа членов (ряд (10.4) называют m – ым остатком исходного ряда (10.1)). 2. Если сходится остаток исходного ряда, то сходится и сам ряд. 3. Если сходится ряд u1 + u2 + … и суммой его является число S, то сходится и ряд а u1 + аu2 + …, причем сумма последнего ряда равна aS. 4. Если сходятся ряды u1 + u2 + …, v1 + v2 +..., имеющие суммы S и s, то сходится и ряд ( u1 + v1) + (u2 + v2) + … причем сумма последнего ряда равна S + s (последний ряд получен почленным сложением исходных рядов). 5. Если ряд u1 + u2 + … сходится, то
Рассмотрим важнейшие достаточные признаки сходимости рядов с положительными членами. 1. Первый признак сравнения. Пусть даны два ряда причем каждый член ряда (1) не превосходит соответствующего члена ряда (2), т.е. un £ vn (n= 1, 2, 3,..). Тогда, если сходится ряд (2), то сходится и ряд (1); если расходится ряд (1), то расходится и ряд (2). Отметим, что в соответствии со свойством (2) рядов, этот признак остается в силе, если неравенства un £ vn выполняются не при всех n, а лишь начиная с некоторого номера n = N. 2. Второй (предельный) признак сравнения. Если существует конечный и отличный от нуля предел 3. Признак Даламбера. Если для ряда 4. Признак Коши (радикальный). Если для ряда 5. Интегральный признак. Если f(x) при x ³ 1 – непрерывная положительная и монотонно убывающая функция, то ряд Сходимость знакочередующихся рядов (рядов вида исследуется с помощью признака Лейбница: знакочередующийся ряд сходится, если абсолютные величины его членов убывают, а общий член стремится к нулю, т.е. если выполняются следующие два условия: 1. u1 > u2 > u3 >… и 2. Если знакочередующийся ряд сходится, то n –ный остаток его удовлетворяет неравенству |Rn| < un+1, важному в приближенных вычислениях. Знакочередующийся ряд – это частный случай знакопеременного ряда (с произвольным чередованием знаков членов). Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин его членов. Если знакопеременный ряд cходится, а ряд, составленный из абсолютных величин его членов, расходится, то исходный ряд называется условно сходящимся рядом. Отметим, что если ряд сходится условно, то при перестановке бесконечного множества его членов сумма ряда может измениться. (В частности, условно сходящийся ряд можно превратить в расходящийся ряд).
Функциональные ряды. Ряд u1(х) + u2(х) + …+ un(х) +... =
Функциональный ряд называют равномерно сходящимся в некоторой области, если для любого сколь угодно малого e > 0 найдется такое целое положительное N, что при n ³ N выполняется неравенство |Rn(x)| < e для любого х из этой области. Сумма S(x) равномерно сходящегося ряда есть функция непрерывная в этой области. Достаточное условие равномерной сходимости (признак Вейерштрасса): Если функции u1(х), u2(х), …, un(х),... по абсолютной величине не превосходят в некоторой области положительных чисел а1, а2, …, а n,..., причем числовой ряд Равномерно сходящиеся ряды обладают следующими свойствами: 1. Если некоторой области и имеет сумму S(x), то принадлежит рассматриваемой области) сходится и имеет сумму 2. Если функции un (х) – непрерывны в некоторой области и имеют в ней производные un`(х) то, если в этой области ряд Степенные ряды. Степенным называют функциональный ряд вида а0 + а1(х – а) + а2(х – а)2 + …+ аn(x – a)n +... = где а и аn действительные числа. Числа аn называют коэффициентами ряда. Основное свойство степенных рядов определяется теоремой Абеля: Если степенной ряд сходится при х = х0, то он сходится (и притом абсолютно) при всяком значении х, удовлетворяющем неравенству | x – a| < |x0 – a|. Одно из следствий теоремы Абеля - существование для всякого степенного ряда интервала сходимости | x – a | < R (a – R < x < a + R) с центром в точке а. Внутри этого интервала ряд абсолютно сходится, вне его – расходится. На концах интервала, в точках х = а ± R, различные степенные ряды ведут себя по разному: могут сходиться (абсолютно или условно) или расходиться на любом или обоих концах интервала. Число R (половину длины интервала сходимости) называют радиусом сходимости степенного ряда. В частных случаях радиус сходимости может быть равен нулю или стремиться к бесконечности. Если R = 0 то степенной ряд сходится лишь при х = а (в одной точке), если же R ® ¥, то ряд сходится на всей числовой оси. Для отыскания интервала и радиуса сходимости степенного ряда можно использовать следующие способы. 1. Если среди коэффициентов an ряда нет равных нулю, (ряд содержит все целые положительные степени разности х – а), то
при условии, что этот предел (бесконечный или конечный) существует. (Соотношение (10.7) несложно получить из признака сходимости Даламбера). 2. Если общий член ряда имеет вид un = an(x – a)pn, где р = 2, 3, … – целое положительное число, то 3. Если среди коэффициентов ряда an есть равные нулю и последовательность показателей степени любая, то можно воспользоваться формулой 4. Применить непосредственно признаки Даламбера или Коши (радикальный) к ряду, составленному из абсолютных величин членов исходного ряда Отметим еще одно важное свойство степенных рядов: ряды, полученные почленным дифференцированием и интегрированием степенного ряда имеют тот же интервал сходимости и их сумма внутри интервала сходимости равна соответственно производной и интегралу от суммы первоначального ряда.
Ряды Тейлора и Маклорена. В разделе 3.3 обсуждалось представление функции f(x), имеющей все производные по (n + 1) – ю включительно, с помощью формулы Тейлора в окрестности точки х = а. Если функция f(x) бесконечно дифференцируема в окрестности точки х = а, то число n можно брать сколь угодно большим. Если Ряд Тейлора сходится к данной функции. Если в (10.12) положим а = 0, то получим частный случай ряда Тейлора, называемый рядом Маклорена: Для всякой элементарной функции существуют такие а и R, что в интервале (а – R, a + R) она разлагается в ряд Тейлора. Приведем наиболее часто используемые разложения.
Последнее выражение называют биномиальным рядом и использовать его можно: при m ³ 0, если х Î [–1; 1] при –1 < m < 0, если х Î (–1; 1] при m £ –1, если х Î (–1; 1).
Приложение рядов к вычислению функций и интегралов. Приведенные соотношения позволяют находить значения соответствующих функций от произвольного аргумента. Пример: Тогда по формуле (10.18). Полученный знакочередующийся ряд удовлетворяет условиям признака Лейбница и сумма отброшенных членов ряда не превышает по абсолютной величине первого отброшенного члена. Это значит, что, учитывая необходимое число членов ряда, искомое значение можно вычислить с любой требуемой точностью. По такому же алгоритму могут решаться и другие подобные задачи. С помощью рядов можно вычислять и приближенные значения определенных интегралов. Подинтегральную функцию представляют в виде ряда Тейлора (полагаем, что функция удовлетворяет необходимым условиям), этот ряд почленно интегрируют и получают новый ряд, сходящийся к искомой функции.
Пример: вычислить с точностью до 10–3:
(Можно отбросить уже 3–й член, поскольку он меньше требуемой точности). Ряды Фурье. Функциональный ряд вида называется тригонометрическим рядом. Постоянные a0, an, bn называются коэффициентами тригонометрического ряда. Если ряд (10.19) сходится, то его сумма j(х) – периодическая функция с периодом 2p, т.е. j(х) = j(х + 2p). Вопрос – можно ли (и при каких условиях) найти тригонометрический ряд, сходящийся к заданной функции f(x) = f(x + 2p)? Предположим, что функция f(x) представлена рядом (10.19), сходящимся к данной функции на интервале (–p; p), т.е. Предположим также, что интеграл от функции f(x) равен сумме интегралов от членов ряда (10.20) (Это предположение справедливо для равномерно сходящихся в некоторой области Х рядов вида
Прежде чем вычислить другие коэффициенты ряда, приведем несколько формул: Если n и k – целые числа и n ¹ k, то
Умножим обе части (10.20) на coskx (k ¹ 0):
Этот ряд равномерно сходится и почленно интегрируется на любом отрезке. Проинтегрируем (10.20`) в пределах от –p; p:
Умножая обе части (10.20) на sinkx и интегрируя в тех же пределах, получим Коэффициенты, определенные соотношениями (10.21) – (10.23) называют коэффициентами Фурье функции f(x), а тригонометрический ряд (10.19) с такими коэффициентами – рядом Фурье функции f(x). Приведем теорему Дирихле о достаточных условиях представимости функции f(x) рядом Фурье. Если функция f(x) в интервале [– p; p] имеет конечное число экстремумов и является непрерывной, за исключением, может быть, конечного числа точек разрыва первого рода (т.е. удовлетворяет так называемым условиям Дирихле), то ряд Фурье в каждой точке интервала [– p; p] сходится к функции f(x). (Отметим, что если х0 – точка разрыва первого рода функции f(x), то сумма ряда Фурье в точках непрерывности равна значению функции, а в точке х0 За значение f(x) на каждой из границ интервала [–p; p] принимают величину
|
|||||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 184; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.181.209 (0.352 с.) |
 , где х1, х2, …, хn- неизвестные функции переменной t,
, где х1, х2, …, хn- неизвестные функции переменной t, откуда
откуда  и
и 
 .
. откуда
откуда  .
.
 . Продифференцируем (1) по t:
. Продифференцируем (1) по t:  . Подставив
. Подставив 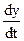 из (2) получим:
из (2) получим:  - решая линейное уравнение второго порядка
- решая линейное уравнение второго порядка  найдём к2-1=0; и к1,2=
найдём к2-1=0; и к1,2= 


 подставив в (3) получим
подставив в (3) получим  и
и  Подставив х в (1) найдём
Подставив х в (1) найдём 
 ; 3)
; 3)  ;
; ; 4)
; 4)  .
. ?
? ; 3)
; 3)  ;
; ; 4)
; 4)  .
. ; 2)
; 2)  .
. и 2)
и 2)  . Что есть общее решение и общий интеграл дифференциального уравнения?
. Что есть общее решение и общий интеграл дифференциального уравнения? ; 2)
; 2)  ; 3)
; 3)  .
. . Решение уравнения?
. Решение уравнения? ; 3)
; 3)  ;
; ; 4)
; 4)  .
. ; 2)
; 2)  ; 3)
; 3)  .
. . Решение?
. Решение? ; 2)
; 2)  ; 3)
; 3)  .
. ; 2)
; 2) 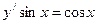 ; 3)
; 3)  .
. ; Его следует решить используя замену переменной вида:
; Его следует решить используя замену переменной вида: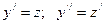 ; 2)
; 2)  .
. и начальные условия:
и начальные условия:  ,
,  . Искомое частное решение:
. Искомое частное решение: ; 3)
; 3)  ;
; ; 4)
; 4)  .
. . Оно:
. Оно: ,
,  . Можно ли составить из них общее решение?
. Можно ли составить из них общее решение? . Его общее решение имеет вид:
. Его общее решение имеет вид: ; 2)
; 2)  ; 3)
; 3)  .
. ; 2)
; 2)  ; 3)
; 3)  .
. и начальные условия
и начальные условия 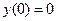 ;
; 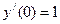 ; Искомое решение:
; Искомое решение: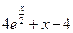 ; 2)
; 2)  ; 3)
; 3)  .
. ; 2)
; 2) 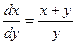 ; 3)
; 3)  . Какое из них можно называть интегрируемыми комбинациями?
. Какое из них можно называть интегрируемыми комбинациями?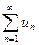 , где S – символ суммирования, сверху и снизу – пределы суммирования (номера первого и последнего членов), n – текущий индекс (номер члена).
, где S – символ суммирования, сверху и снизу – пределы суммирования (номера первого и последнего членов), n – текущий индекс (номер члена). . Число S называют суммой ряда. Если n –ная частичная сумма ряда при n ® ¥ не стремится к конечному пределу, то ряд называют расходящимся.
. Число S называют суммой ряда. Если n –ная частичная сумма ряда при n ® ¥ не стремится к конечному пределу, то ряд называют расходящимся. (10.3).
(10.3). , т.е. при n ® ¥ предел общего члена сходящегося ряда равен нулю. Это необходимый признаксходимости; если он выполняется – ряд может сходиться (а может и расходиться), а если
, т.е. при n ® ¥ предел общего члена сходящегося ряда равен нулю. Это необходимый признаксходимости; если он выполняется – ряд может сходиться (а может и расходиться), а если  – ряд расходится. Ряд
– ряд расходится. Ряд 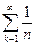 (10.5), называемый гармоническим, расходится (при том, что
(10.5), называемый гармоническим, расходится (при том, что 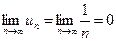 ).
).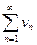 (2),
(2), , то оба ряда
, то оба ряда  , то этот ряд сходится при С < 1 и расходится при C > 1. При С = 1 вопрос о сходимости остается открытым (необходимо применить другой признак).
, то этот ряд сходится при С < 1 и расходится при C > 1. При С = 1 вопрос о сходимости остается открытым (необходимо применить другой признак). , то этот ряд сходится при D < 1 и расходится пр и D > 1. Случай D = 1 требует дополнительного исследования.
, то этот ряд сходится при D < 1 и расходится пр и D > 1. Случай D = 1 требует дополнительного исследования. .
. , где un > 0)
, где un > 0) .
. , члены которого – функции от х, называется функциональным. При конкретных значениях х функции принимают различные значения и каждому значению х соответствует числовой ряд, сходящийся или расходящийся. Совокупность значений х, при которых функции un(x) определены и ряд
, члены которого – функции от х, называется функциональным. При конкретных значениях х функции принимают различные значения и каждому значению х соответствует числовой ряд, сходящийся или расходящийся. Совокупность значений х, при которых функции un(x) определены и ряд  . Эту величину, являющуюся функцией х, называют суммой функционального ряда и обозначают через S(x). Обозначив сумму первых n членов ряда через Sn(x), можно записать S(x) = Sn(x) + Rn(x), где Rn(x) =
. Эту величину, являющуюся функцией х, называют суммой функционального ряда и обозначают через S(x). Обозначив сумму первых n членов ряда через Sn(x), можно записать S(x) = Sn(x) + Rn(x), где Rn(x) =  n –ый остаток функционального ряда. Если функциональный ряд сходится, то остаток его Rn(x) стремится к нулю при n ® ¥.
n –ый остаток функционального ряда. Если функциональный ряд сходится, то остаток его Rn(x) стремится к нулю при n ® ¥. сходится, то функциональный ряд
сходится, то функциональный ряд 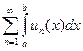 (интервал [ a, b]
(интервал [ a, b]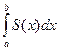 .
. сходится равномерно, то его сумма равна производной от суммы первоначального ряда:
сходится равномерно, то его сумма равна производной от суммы первоначального ряда: 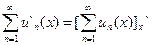 .
. (10.6),
(10.6), (10.7)
(10.7) (10.8).
(10.8). (10.9) (В ней используются значения an отличные от нуля). Соотношение (10.9) можно использовать и в случаях 1 и 2.
(10.9) (В ней используются значения an отличные от нуля). Соотношение (10.9) можно использовать и в случаях 1 и 2. , где u0 = a0, un(x) = an(x –a)N, где зависимость N от n может быть любой, а через аn обозначается не коэффициент при (х – а)n, а коэффициент n – го члена ряда. В этом случае интервал сходимости находят из неравенств
, где u0 = a0, un(x) = an(x –a)N, где зависимость N от n может быть любой, а через аn обозначается не коэффициент при (х – а)n, а коэффициент n – го члена ряда. В этом случае интервал сходимости находят из неравенств  (10.10) или
(10.10) или  (10.11).
(10.11). (3.31), где остаточный член Rn может быть представлен в виде
(3.31), где остаточный член Rn может быть представлен в виде  (форма Лагранжа).
(форма Лагранжа). , то, переходя в (3.31) к пределу при n ® ¥, получим справа бесконечный ряд Тейлора:
, то, переходя в (3.31) к пределу при n ® ¥, получим справа бесконечный ряд Тейлора:  (10.12).
(10.12). (10.12`).
(10.12`). ; х Î (–¥, ¥) (10.13)
; х Î (–¥, ¥) (10.13) ; х Î (–¥, ¥) (10.14)
; х Î (–¥, ¥) (10.14) ; х Î (–¥, ¥) (10.15)
; х Î (–¥, ¥) (10.15) ; х Î (–1; 1) (10.16)
; х Î (–1; 1) (10.16) ; х Î [–1; 1] (10.17)
; х Î [–1; 1] (10.17) (10.18)
(10.18) . Очевидно, 29 = 27 + 2 = 27(1 + 2/27).
. Очевидно, 29 = 27 + 2 = 27(1 + 2/27).

 (10.19)
(10.19) (10.20).
(10.20). ). Проинтегрируем (10.20) в пределах от (–p; p)
). Проинтегрируем (10.20) в пределах от (–p; p) , вычисляя отдельно каждый интеграл в правой части:
, вычисляя отдельно каждый интеграл в правой части: 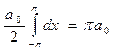 ;
;
 , откуда
, откуда  (10.21)
(10.21) ;
;  ;
;  . Если n = k, то
. Если n = k, то  ;
; ;
; 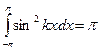 ;
; (10.20`).
(10.20`). ; откуда
; откуда  (10.22).
(10.22). , откуда
, откуда  (10.23).
(10.23).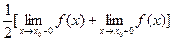 (10.24).
(10.24). (10.24 `).
(10.24 `).


