
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Однородные уравнения первого порядка.
Функцию f(x, y) называют однородной m – го измерения, если при любом l справедливо равенство f(lx, ly) = lm f(x, y). Пример:
Уравнение вида y` = f(x, y) (или приводимое к нему) называют однородным, если f(x, y) – однородная функция нулевого измерения, т.е. f(lx, ly)=f(x, y). С помощью подстановки у = tх однородное уравнение приводится к уравнению с разделяющимися переменными относительно новой функции t = y/x. Пример:
откуда y= xlnC|y|.
Линейные дифференциальные уравнения первого порядка – это уравнения вида y` + P(x)y = Q(x) (9.4) (y и y` входят в первых степенях не перемножаясь между собой). Если Q(x) ¹ 0, уравнение называется линейным неоднородным, а если Q(x) = 0 – линейным однородным. (Если в уравнении (9.4) положим Q(x) = 0, то получим соответствующее ему однородное уравнение). Общее решение линейного однородного уравнения y` + Р(х)у = 0 легко получается разделением переменных:
Общее решение линейного неоднородного уравнения можно найти: а) Методом Лагранжа (методом вариации произвольной постоянной) – исходя из решения соответствующего однородного уравнения и варьируя произвольную постоянную, т.е полагая
б) Методом Бернулли - подстановкой у = uv, где u и v – неизвестные функции от х, исходное уравнение преобразуется к виду u`v + uv` + P(x)uv = Q(x) (1) или u[v` + P(x)v] + vu` = Q(x) (2). Одна из неизвестных функций (v, например) может быть выбрана произвольно. Определим ее из условия v` + P(x)v = 0 (3), откуда
Произведение произвольныx постоянных есть произвольная постоянная; без потери общности, можно положить С1 = 1; т.е. Примеры: 1. Решим уравнение y`cos2x + y = tgx методом Лагранжа. Соответствующее однородное уравнение: y`cos2x + y = 0. Разделяя переменные, получим
2. Решим уравнение y` – 2y(x + 1) = (x + 1)3 методом Бернулли. Полагаем y = uv, y` = u`v + uv` и, подставляя, найдем u`v + uv` – 2uv(x + 1) = (x + 1)3
откуда u`v – u(v` – 2v(x + 1)) = (x + 1)3 (1). Положим v` – 2v(x + 1) = 0, откуда
du = (x + 1)dx и u = (x + 1)2 / 2 + C, откуда y = uv = (x + 1)4/2 + C(x + 1)2.
|
|||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 123; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.120.109 (0.005 с.) |
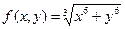
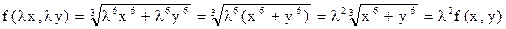 , т.е., исходная функция – однородная второго измерения.
, т.е., исходная функция – однородная второго измерения. (1). Положим y = tx, откуда y` = t + xt`. Подставим в (1):
(1). Положим y = tx, откуда y` = t + xt`. Подставим в (1): . Разделяя переменные
. Разделяя переменные и интегрируя получим:
и интегрируя получим:  (Логарифм произвольной постоянной есть произвольная постоянная, что и используем для упрощения записи). Возвращаясь к исходной функции получим:
(Логарифм произвольной постоянной есть произвольная постоянная, что и используем для упрощения записи). Возвращаясь к исходной функции получим: ,
, , где С – произвольная постоянная.
, где С – произвольная постоянная. , где С(х) подлежащая определению дифференцируемая функция от х. Для нахождения С(х) нужно подставить у в исходное уравнение, что приводит к соотношению
, где С(х) подлежащая определению дифференцируемая функция от х. Для нахождения С(х) нужно подставить у в исходное уравнение, что приводит к соотношению 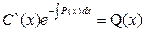 откуда
откуда  , где
, где 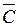 – произвольная постоянная. Искомое общее решение неоднородного уравнения примет вид
– произвольная постоянная. Искомое общее решение неоднородного уравнения примет вид (9.5).
(9.5).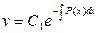 (4). Подставляя (4) с учетом (3) в (2) получим
(4). Подставляя (4) с учетом (3) в (2) получим  , откуда
, откуда 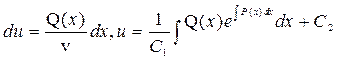 и
и
 и
и 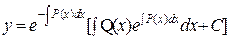 .
. , откуда, интегрируя, найдем
, откуда, интегрируя, найдем 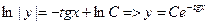 . Решение исходного уравнения ищем в виде у = С(х)е–tgx. Подставляя в исходное уравнение у` = C`(x)e–tgx – C(x)e–tgx (1/cos2x) получим:
. Решение исходного уравнения ищем в виде у = С(х)е–tgx. Подставляя в исходное уравнение у` = C`(x)e–tgx – C(x)e–tgx (1/cos2x) получим:  и
и 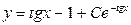
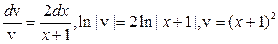 . Подставим в (1): u`(x+1)2 = (x + 1)3 =>
. Подставим в (1): u`(x+1)2 = (x + 1)3 =>


