
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приложения определенного интеграла к задачам практики.Содержание книги
Поиск на нашем сайте
Легко видеть, что площадь фигуры, ограниченной кривыми y = f1(x) и y = f2(x); 0 £ f 2(х) £ f1(x) и прямыми х = а и х = b определится соотношением
 (6.9). (6.9).
В полярных координатах площадь криволинейного сектора, ограниченная кривой r = r(j) и двумя полярными радиусами j = a и j = b(a < b) определится выражением а площадь фигуры, ограниченной кривыми r1(j), r2(j), r2(j) £ r1(j) и радиусами j = a и j = b выражением
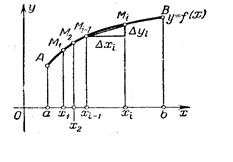 2. Длина дуги плоской кривой. Пусть на плоскости дана кривая y = f(x). Найдем длину дуги АВ этой кривой между прямыми х = а и х = b (рис.6.4.). Возьмем на дуге точки А, М1, …, Мi, …, В с абсциссами х0 =а, х1, …xi, …,xn= b и проведем хорды А М1, М1М2, …, Мi–1Mi, …, Mn–1 B, длины которых обозначим через DSi. Получим ломаную АМ1М2 …Мi …В, вписанную в дугу АВ. Длина ломаной равна 2. Длина дуги плоской кривой. Пусть на плоскости дана кривая y = f(x). Найдем длину дуги АВ этой кривой между прямыми х = а и х = b (рис.6.4.). Возьмем на дуге точки А, М1, …, Мi, …, В с абсциссами х0 =а, х1, …xi, …,xn= b и проведем хорды А М1, М1М2, …, Мi–1Mi, …, Mn–1 B, длины которых обозначим через DSi. Получим ломаную АМ1М2 …Мi …В, вписанную в дугу АВ. Длина ломаной равна 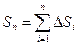 . Длиной S дуги АВ называется предел, к которому стремится длина вписанной ломаной, когда длина ее наибольшего звена стремится к нулю: . Длиной S дуги АВ называется предел, к которому стремится длина вписанной ломаной, когда длина ее наибольшего звена стремится к нулю: 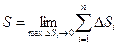 . .
Если на отрезке [a, b] функции f(x) и f `(x) непрерывны (кривая – гладкая), то этот предел существует и равен Если гладкая кривая задана в полярных координатах уравнением r = r(j) (a £ j £b), длина дуги равна 3. Вычисление объема тела по параллельным сечениям. Если площадь сечения тела плоскостью, перпендикулярной оси Ох, может быть выражена как функция от х, т.е. в виде S = S(x), то объем части тела, заключенной между плоскостями х = а и x = b, определится формулой 4. Объем тела вращения. Если криволинейная трапеция, ограниченная кривой y = f(x) и прямыми х = а и х = b, вращается вокруг оси Ох, то объем тела вращения определится соотношением Если вокруг оси Ох вращается фигура, образованная кривыми y = f1(x) и y = f2(x) (0 £ f1(x) £ f2(x)) и прямыми х = а и х = b, то объем тела вращения
5. Поверхность тела вращения. Если дуга гладкой кривой y = f(x) (а £ х £ b) вращается вокруг оси Ох, то площадь поверхности вращения вычисляется по формуле 6. Работа и давление. Работа переменной силы F = f(x), действующей по оси Ох на отрезке [a, b] вычисляется по формуле
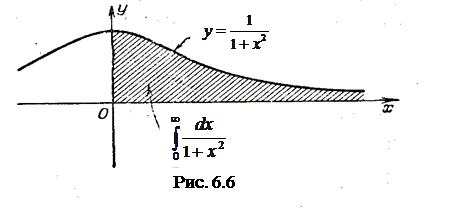
Пример: Какое давление испытывает прямоугольная пластина длиной а и шириной b (a > b), если она наклонена к поверхности жидкости под углом a и ее большая сторона находится на глубине h (рис.6.5)? Площадь выделенной на глубине х элементарной полоски равна Несобственные интегралы. Интеграл с бесконечными пределами. Рассмотрим интеграл и называют несобственным интегралом от функции f(x) на интервале [a, ¥). Если этот предел существует и конечен- интеграл называют сходящимся; если же предел не существует или равен бесконечности – расходящимся. Геометрический смысл в случае f(x) ³ 0 – площадь неограниченной области, заключенной между линиями y = f(x), х = а и у = 0 (ось Ох). Пример: (рис.6.6)
Аналогично определяются интегралы: и Бывает достаточно установить, сходится или расходится данный интеграл и оценить его значение. Это позволяют сделать следующие теоремы:
1. Если для всех х ³ а выполняется неравенство о £ f(x) £ j(х) и если 2. Если для всех х ³ а выполняется неравенство f(x) ³ j(х) ³ 0, причем 3. Если интеграл Пример: исследовать сходимость
Интеграл от неограниченной функции. Пусть функция y = f(x) определена и непрерывна при а £ х < с, а в точке с испытывает бесконечный разрыв. Интеграл называют несобственным интегралом от неограниченной функции. Если этот предел существует и конечен – интеграл сходящийся, если нет – расходящийся. Аналогично определяются интегралы
(при а < x £ c и Несобственный интеграл (6.19``) называют сходящимся, если существуют оба предела в правой части равенства, и расходящимся, если не существует хотя бы один из них. Для решения вопроса о сходимости несобственных интегралов от разрывных функций и оценки их значений полезны следующие теоремы: 1. Если на отрезке [a, с] функции f(x) и j(х) разрывны в точке с, причем во всех точках этого отрезка j(х) ³ f(x) ³ 0 и Пример: Сходится ли сходится, и, соответственно, сходится исходный интеграл. Тесты 3.10. 1) 0; 2) 3.11. 1) 0; 2) 3.12. 1) 3.13. 1) 3.14. 1) 3.15. Сходится ли 1) 0; 2) 3.16. Сходится ли 1) 0; 2) –3; 3) 2p. 3.17. 1) 3.18. 1) Сходится; 2) Расходится. 3.19. Площадь фигуры, ограниченной линиями 1) 7; 2) –3,5; 3) 4,5; 4) 6,2. 3.20. Объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиями 1) 2)
|
|||||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 242; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.006 с.) |

 1. Площадь плоской фигуры. Площадь криволинейной трапеции, ограниченной кривой y = f(x), прямыми х = а и х = b и отрезком [a, b], (рис.6.3) вычисляется по формуле
1. Площадь плоской фигуры. Площадь криволинейной трапеции, ограниченной кривой y = f(x), прямыми х = а и х = b и отрезком [a, b], (рис.6.3) вычисляется по формуле  (6.8).
(6.8).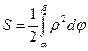 (6.10),
(6.10),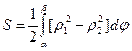 (6.10`).
(6.10`).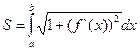 (6.11).
(6.11). (6.12).
(6.12).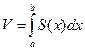 (6.13)
(6.13) (6.14).
(6.14). (6.15).
(6.15). (6.16).
(6.16).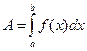 (6.17)
(6.17)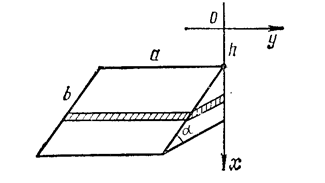
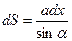 . Следовательно,
. Следовательно, 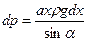 (r – плотность жидкости). Отсюда находим
(r – плотность жидкости). Отсюда находим 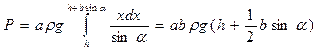 .
. . При переменном b он является непрерывной функцией b. Предел этой функции при b ® ¥ обозначают
. При переменном b он является непрерывной функцией b. Предел этой функции при b ® ¥ обозначают 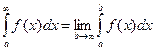 (6.18)
(6.18)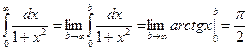 .
.
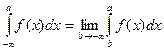 (6.18`)
(6.18`) (6.18``).
(6.18``).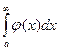 сходится, то сходится и
сходится, то сходится и 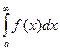 , причем
, причем  сходится, то сходится и
сходится, то сходится и 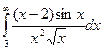 . Подинтегральная функция знакопеременная. Рассмотрим
. Подинтегральная функция знакопеременная. Рассмотрим 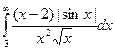 . Очевидно, что
. Очевидно, что 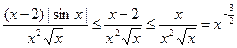 ;
; 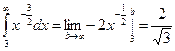 . Исходный интеграл сходится абсолютно.
. Исходный интеграл сходится абсолютно.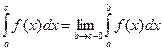 (6.19)
(6.19)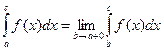 (6.19`)
(6.19`)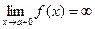 ), и, если функция имеет бесконечный разрыв в точке с внутри отрезка [a, b],
), и, если функция имеет бесконечный разрыв в точке с внутри отрезка [a, b], 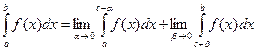 (6.19``).
(6.19``). сходится, то
сходится, то 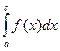 также сходится; 2. Если на отрезке [a, с] функции f(x) и j(х) разрывны в точке с, причем во всех точках этого отрезка f(x) ³ j(х) ³ 0 и
также сходится; 2. Если на отрезке [a, с] функции f(x) и j(х) разрывны в точке с, причем во всех точках этого отрезка f(x) ³ j(х) ³ 0 и  сходится, то сходится (абсолютно) и
сходится, то сходится (абсолютно) и 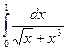 ? Подинтегральная функция разрывна при х = 0. В указанном интервале
? Подинтегральная функция разрывна при х = 0. В указанном интервале 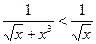 . Несобственный интеграл
. Несобственный интеграл 
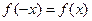 ;
; 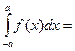
 ; 3)
; 3) 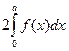 .
.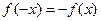 ;
; 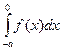 ; 3)
; 3) 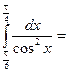
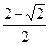 ; 2)
; 2) 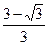 ; 3)
; 3) 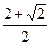 ; 4)
; 4)  .
.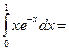
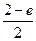 ; 2)
; 2) 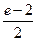 ; 3)
; 3) 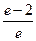 ; 4)
; 4) 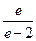 .
.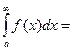
 ; 2)
; 2) 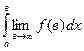 ; 3)
; 3) 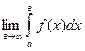 .
. и, если да, то равен:
и, если да, то равен: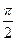 ; 3) 1.
; 3) 1.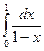 и, если да, то равен:
и, если да, то равен: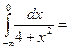
 ; 2)
; 2) 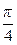 ; 3)
; 3) 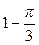 ; 4)
; 4)  .
.
 и
и 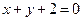 , равна (кв.ед):
, равна (кв.ед):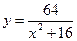 и
и 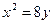 составляет (куб.ед.):
составляет (куб.ед.): ; 3)
; 3)  ;
;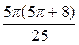 ; 4)
; 4) 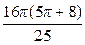 .
.


