
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Собственные значения и собственныеСодержание книги
Поиск на нашем сайте
ФУНКЦИИ ОПЕРАТОРОВ 73. Пусть Решение. Подействуем оператором
74. Покажите, что собственной функцией оператора 75. Найдите собственные функции операторов: а) 76. Найдите собственные значения и собственные функции оператора 77. Покажите, что две разные собственные функции эрмитовского оператора ортогональны. 78. Покажите, что волна де Бройля 79. Покажите, что волны де Бройля 80. Эрмитовский оператор задан в виде матрицы 81. Покажите, что если оператор симметрии системы 82. Какой физический смысл имеет ортогональность собственных функций оператора? А нормированость? 83. В чём состоит физический смысл вырождения собственных функций оператора
5. УРАВНЕНИЕ ШРЕДИНГЕРА.
84. Чем отличается уравнение Шредингера от уравнения диффузии? 85. Почему в левой части уравнения Шредингера стоит частная, а не полная производная по t? 86. Что называется полным набором величин? Сколько величин входит в полный набор? 87. Чем отличается полный набор величин в квантовой механике от полного набора величин в классической механике? 88. Что такое интеграл движения? Какая разница в истолковании интегралов движения в квантовой и классической механике? 89. Что понимают под стационарным состоянием в квантовой механике? Чем это толкование отличается от классического? 90. Если стационарное состояние в квантовой механике меняется со временем, почему оно называется стационарным? 91. Как стационарное квантовое состояние зависит от времени? 92. Выясните зависимость от времени средней величины <A> не зависящего от времени оператора а) не стационарно; б) стационарно. 93. Запишите уравнение Шредингера в энергетическом представлении. 94. Запишите уравнение Шредингера 95. Запишите гамильтониан для следующих микросистем: а) Li, б) Be, в) Li2, г) 96. Покажите, что точный гамильтониан молекул изомеров одинаков. 96а. Почему гамильтонианы молекул изомеров, написанные в адиабатическом приближении, различаются? 97. Покажите, что: а) точный гамильтониан молекулы не меняется при перестановке любой пары частиц молекулы; б) точный гамильтониан левой и правой частей уравнения химической реакции одинаков. 97а. Покажите, что гамильтонианы молекул изомеров, написанные в адиабатическом приближении, изменяются при перестановке различных ядер. 98. Покажите, что из уравнения Шредингера следует закон сохранения массы. 99. Покажите, что из уравнения Шредингера следует закон сохранения электрического заряда. 100. Что в квантовой механике называют: а) потенциальной ямой? б) потенциальным барьером? в) потенциальной стенкой? 101. Напишите уравнение Шредингера для стационарных состояний частицы, имеющей энергию Е и движущейся в потенциале вида (рис. 6). Решение. в) U(x) = - U2 ·(1 - х/а) при 0 £ х £ а, U(x) = U1, при х > а; г) при том же уравнении U(x) = U0, при x < 0; х > 2(b + R); U(x) = 0, при 0 £ х £ b; b + 2R £ х £ 2(b + R); U(x) = - и) в этой задаче можно обойтись одной переменной: расстоянием по окружности. Тогда можно обозначить, например, l = rq. Учитывая, что в одномерном уравнении Шредингера от переменной l можно перейти к переменной q, то есть
уравнение Шредингера можно записать так:
где 102. Обоснуйте качественно вид решений уравнения Шредингера для потенциалов предыдущей задачи. Чем отличаются решения уравнения Шредингера для систем а-г от уравнения Шредингера для частицы в прямоугольной потенциальной яме с бесконечно высокими стенками. 103. Придумайте одномерный потенциал, отличный от а-и задачи 101, и запишите для него уравнение Шредингера. 104. Что такое условия сшивания для волновой функции и каков их физический смысл? Запишите условия сшивания для волновой функции задачи 101 (и). 105. Какие решения временного уравнения Шредингера называют стационарными? Покажите, что такие решения получаются в том случае, когда U не зависит от времени явно. 106. Как изменится волновая функция Y(х, t), описывающая стационарные состояния, если изменить начало отсчета потенциальной энергии на некоторую величину DU? 107. Найдите решения временного уравнения Шредингера для свободной частицы, движущейся с импульсом р в положительном направлении оси Х. 108. То же, что и в предыдущей задаче, но частица движется с импульсом 109. Покажите, что энергия свободно движущейся частицы может иметь любые значения (непрерывный спектр). 110. Частица массы m находится в одномерной прямоугольной потенциальной яме шириной l с бесконечно высокими стенками. Покажите, что собственные значения энергии частицы и ее нормированные собственные функции (0 < x < l) имеют вид:
Решение. Уравнение Шредингера внутри ямы имеет вид:
где
Коэффициенты С1 и С2 находим из граничных условий: y(0)=0; y(l)=0. Из первого граничного условия получаем С1= -С2и y(х)=2i С1 sin kx; из второго граничного условия имеем sinkl=0, kl=np, где n=±1,±2,... Значения n=0 отбрасываем, так как при этом значении y(х) тождественно равно нулю во всех точках внутри ямы, что соответствует отсутствию такого состояния. k = np/l; yn(x) = Сsin (npx/l). Здесь мы воспользовались принципом суперпозиции, умножив Y(х) на постоянное число -0,5i. Коэффициент С находим из условия нормировки: 111. Частица массы m находится в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. Найдите энергию Е частицы в стационарном состоянии: а) описываемом волновой функцией б) если ширина ямы l и число узлов волновой функции Y(х) равно N. 112. Частица находится в одномерной потенциальной прямоугольной яме с бесконечно высокими стенками. Ширина ямы l. Найдите нормированные y-функции стационарных состояний частицы, взяв начало отсчета координаты х в середине ямы. 113. Частица находится в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. Найдите: а) массу частицы, если ширина ямы l и разность энергий 3-го и 2-го энергетических уровней равна DЕ; б) квантовое число n энергетического уровня частицы, если интервалы энергии до соседних с ним уровней (верхнего и нижнего) относятся как h:1, где h=1,4. 114. Частица массы m находится в основном состоянии в одномерной потенциальной яме шириной l с бесконечно высокими стенками. Найдите: а) силу давления, которую оказывает частица на стенку; б) работу, которую нужно совершить, чтобы медленно сжать яму в h раз. 115. Частица находится в основном состоянии в одномерной потенциальной яме шириной l с бесконечно высокими стенками. Найдите вероятность пребывания частицы в области l/3 < x < 2l/3. 116. Частица массы m находится в основном состоянии в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. Максимальное значении плотности вероятности местонахождения частицы равно Pm. Найдите ширину l ямы и энергию Е частицы в данном состоянии. 117. Частица массы m находится в двухмерной прямоугольной потенциальной яме с бесконечно высокими стенками. Координаты x, y частицы лежат в пределах 0<x<a, 0<y<b, где a и b - стороны ямы. Найдите собственные значения энергии и нормированные собственные функции частицы. 118. Определите в условиях предыдущей задачи вероятность нахождения частицы с наименьшей энергией в области 0<x<a/3, 0<y<b/3. 119. Частица массы m находится в двухмерной квадратной яме с бесконечно высокими стенками. Сторона ямы равна l. Найдите значения энергии Е частицы для первых четырех уровней. 120. Частица массы m находится в основном состоянии в двухмерной квадратной потенциальной яме с бесконечно высокими стенками. Найдите энергию Е частицы, если максимальное значение плотности вероятности местонахождения частицы равно Pm. 121. Частица массы m находится в трехмерной прямоугольной потенциальной яме с абсолютно непроницаемыми стенками. Длины ребер ямы равны a, b, c. Найдите собственные значения энергии частицы. 122. Что называется квантовым осциллятором? Чем отличается квантовый гармонический осциллятор от классического?
ВЫРОЖДЕНИЕ
123. Что называется вырожденным состоянием? Покажите, что если функции y1 и y2 являются собственными функциями оператора 124. Почему возбужденные состояния атома водорода вырождены? 125. Покажите, что если гамильтониан системы не меняется при некоторой операции симметрии, то состояние системы вырождено. 126. Подсчитайте кратность вырождения состояния электрона в атоме водорода при n=3: а) без учета спина; б) с учетом спина. 127. Почему в трехмерной прямоугольной потенциальной яме состояния электрона вырождены?
МАТРИЧНАЯ ФОРМА УРАВНЕНИЙ
128. Как записывается оператор в матричной форме? Что понимают под матричным элементом оператора? 129. Что представляет собой матрица оператора в собственном базисе? 130. Дайте определение эрмитовской матрицы: симметричной, положительно определенной. Почему матрица гамильтониана должна быть эрмитовской? 131. Что понимают под диагонализацией матрицы и зачем необходимо диагонализировать матрицы операторов физических величин? 132. Как можно привести матрицу оператора к диагональному виду? 133. Найдите собственные значения матрицы 134. Что такое собственный вектор матрицы? Найдите собственные векторы матрицы задачи 133. АТОМ ВОДОРОДА
135. Почему задачу о движении электрона в атоме Н удается решить точно, а для атома гелия это не возможно? 136. Запишите наиболее общий вид волновой функции, описывающей электрон в поле протона. Почему угловая часть этой функции зависит от квантовых чисел l и m? Почему радиальная часть данной функции зависит от n и l? 137. Найдите наиболее вероятное расстояние электрона 1S от ядра в атоме Н. То же для электрона в состоянии 2S. 138. Найдите среднее расстояние 1S-электрона в атоме водорода от ядра. 139. Постройте угловую зависимость от угла q орбитали электрона атома водорода 140. Координатная часть волновой функции электрона в 2S-состоянии атома водорода имеет вид:
где b - постоянная, a0 - радиус первой Боровской орбиты. Постройте: а) график этой функции в зависимости от r; б) график зависимости вероятности нахождения электрона от расстояния r до ядра. Установите положения максимумов плотности вероятности в единицах радиуса Боровской орбиты (r/a0). 141. Координатная часть волновой функции электрона в 3S-состоянии атома водорода имеет вид:
где b-постоянная, a0 -радиус первой Боровской орбиты. Постройте: а) график этой функции в зависимости от r; б) график зависимости плотности вероятности нахождения электрона от расстояния r до ядра. Установите положения максимумов плотности вероятности в единицах радиуса Боровской орбиты (r/a0). 142. Радиальная часть волновой функции электрона атома водорода в состоянии 2рz имеет вид:
где b - постоянная, a0 - радиус первой Боровской орбиты. Построить: а) график этой функции в зависимости от r; б) график зависимости плотности вероятности нахождения электрона от расстояния r до ядра. Установите положения максимумов плотности вероятности в единицах радиуса Боровской орбиты (r/a0). 143. Радиальная часть волновой функции электрона в состоянии 3рz атома водорода имеет вид:
где b - постоянная, a0 - радиус первой Боровской орбиты. Построить: а) график этой функции в зависимости от r; б) график зависимости плотности вероятности нахождения электрона от расстояния r до ядра. Установите положения максимумов плотности вероятности в единицах радиуса Боровской орбиты (r/a0). 144. Постройте зависимость вероятности нахождения электрона в состоянии 1S от его расстояния r до ядра. 145. Постройте зависимость орбиталей 1S, 2S от углов q и j. Что означает изображение 1S-AO в виде сферы? Почему сфера для 2S-AO имеет бóльшие размеры, чем сфера, изображающая 1S-AO? 146. Постройте угловые зависимости 147. Почему полная энергия электрона в атоме водорода отрицательна? Что означала бы положительность этой энергии? 148. В атоме водорода уровни энергии электрона при n>1 вырождены по орбитальному квантовому числу l, а в многоэлектронных атомах это вырождение снимается. Почему? 149. Один из эффективных методов преобразования матриц к диагональному виду - метод вращений. Покажите, что матрицу Н= 150. Найдите частоту перехода электрона в атоме водорода между уровнями 1S®2P. ТЕОРИЯ ВОЗМУЩЕНИЙ
151. Что понимают под оператором возмущения? 152. В каком смысле говорят о необходимости малости возмущения? 153. Чему равна поправка к энергии системы в первом и во втором приближениях теории возмущений? 154. Состояние некоторой системы описывается волновыми функциями y1, y2, y3, y4, и соответствующими собственными значениями Е1=1, Е2=2, Е3=3, Е4=4. Матричные элементы оператора возмущения равны: W11=0,4; W22=0,3; W33=0,2; W44=0,1; W12=W13=0,1; W23=0,2; W14=W24=0. Найти: а) поправки к уровням энергии в первом и во втором приближениях теории возмущений; б) поправки первого приближения к волновым функциям; в) точные собственные значения возмущенной задачи; г) нормированные волновые функции в первом приближении теории возмущений.
|
||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 391; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.186.247 (0.009 с.) |

 . При каком значении Ln функция Yn = sin nx является решением уравнения
. При каком значении Ln функция Yn = sin nx является решением уравнения 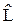 Yn = Ln Yn?
Yn = Ln Yn? n cos nx = - n2 sin nx; Ln = - n2.
n cos nx = - n2 sin nx; Ln = - n2. предыдущей задачи является функция Y(x) = с1 sin nx + с2 cos nx, где с1 и с2 - произвольные постоянные.
предыдущей задачи является функция Y(x) = с1 sin nx + с2 cos nx, где с1 и с2 - произвольные постоянные. ; б)
; б)  .
. , если для оператора
, если для оператора  они равны En и Yn.
они равны En и Yn.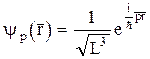 является собственной функцией оператора кинетической энергии частицы
является собственной функцией оператора кинетической энергии частицы 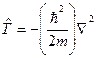 .
. и
и  ортогональны, но относятся к одному и тому же собственному значению
ортогональны, но относятся к одному и тому же собственному значению 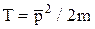 . Каков физический смысл вырождения состояний оператора кинетической энергии?
. Каков физический смысл вырождения состояний оператора кинетической энергии? . Определите собственные значения и собственные функции оператора
. Определите собственные значения и собственные функции оператора 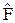 .
.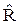 оставляет неизменным гамильтониан, то состояния системы вырождены.
оставляет неизменным гамильтониан, то состояния системы вырождены.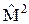 ?
?
 , если состояние частицы:
, если состояние частицы: , е) Н2О.
, е) Н2О.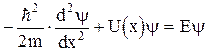 , где U(x) = U0, при x < 0,
, где U(x) = U0, при x < 0, , при b < x < b + 2R;
, при b < x < b + 2R; ,
, ,
, , а 0 £ q £ 2p.
, а 0 £ q £ 2p.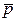 в произвольном направлении.
в произвольном направлении.
 или
или  , (1)
, (1)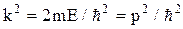 . Решение уравнения (1) имеет вид
. Решение уравнения (1) имеет вид .
. dx=1, откуда
dx=1, откуда  , а из условия
, а из условия  находим
находим  .
. , где k - заданная постоянная, х - расстояние от одного края ямы;
, где k - заданная постоянная, х - расстояние от одного края ямы;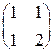 .
. в плоскости XZ.
в плоскости XZ.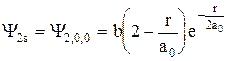 ;
;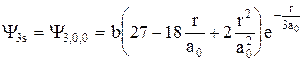 ;
; ;
; ;
;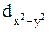 и
и  -AO на плоскостях.
-AO на плоскостях. можно привести к диагональному виду преобразованием подобия с матрицей поворота плоскости системы декартовых координат на 45°.
можно привести к диагональному виду преобразованием подобия с матрицей поворота плоскости системы декартовых координат на 45°.


