
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Измерения. Соотношения неопределенности
45. Сформулируйте постулат об измерении. 46. Пусть частица находится в состоянии y. Какова должна быть эта функция, чтобы некоторая физическая величина в результате измерения не давала разброса значений? 47. Как узнать теоретически, дает ли в состоянии y величина L разброс значений? 48. Пусть при единичном измерении интересующей нас величины L мы получили значение L=Lk. Можно ли на основании этого утверждать, что до этого измерения частица находилась в таком состоянии, что L равнялась Lk? 49. Пусть частица находится в состоянии y(x,t), а функции íjn(x)ý являются собственными функциями некоторого оператора
Ответьте: а) зависят ли коэффициенты Сn от х? б) зависят ли коэффициенты Сn от t? в) какой физический смысл имеют коэффициенты Сn? г) как из (1) выразить Сn? д) каковы математические основы записи (1)? е) что является физической основой записи (1)? 50. Частица находится в состоянии
где Ответьте: а) какие величины будут получаться при измерении L? б) какова вероятность получить при измерении значения L1, L2, L3, L4, L5, L6, L7? 51. Волновая функция частицы не удовлетворяет уравнению
Может ли в результате измерения получиться величина Lk? С какой вероятностью? 52. Общей собственной функцией операторов
Каковы следствия этого факта? Что это значит? Каков будет результат измерения 53. Пусть величина в некотором состоянии может принимать два значения - L1 и L2. Будут ли вероятности их одинаковы? 54. Можно ли одновременно точно измерить полную энергию частицы Е и ее потенциальную энергию U? Кинетическую энергию Т и потенциальную U? 55. Могут ли одновременно точные значения иметь величины x и pх? 56. Показать, что измерение координаты x частиц с помощью узкой щели шириной b вносит неопределенность в их импульсы Dрх такую, что Dх · Dрx ³ h. Решение. Измерение координаты x частиц путем сужения щели b приводит к дифракции частиц (рис. 3), при которой появляется неопределенность в импульсе Dрх вдоль оси x: Dрх»
Dрх
b Рис. 3. на щели, тем меньше Dl и больше Dрх»
Dх · Dрх» h.
57. Плоский поток частиц падает нормально на диафрагму с двумя узкими щелями, образуя на экране дифракционную картину (рис. 4). Показать, что попытка определить, через какую щель прошла та или иная частица (например, с помощью введения индикатора И), приводит к разрушению дифракционной картины. Для простоты считать углы дифракции малыми.
Х
z I(x)
И
Рис. 4.
Решение. Сравним неопределённость Dpx, вносимую при измерении индикатором И, с той (Dp’x), которая необходима, чтобы дифракционная картина не разрушилась. Чтобы установить, через какую щель прошла частица, ее x-координата должна быть определена индикатором И с погрешностью Dх < Dрх ³ 58. Сравнить скорость электрона на первой Боровской орбите с неопределенностью скорости электрона в атоме водорода, полагая размер атома порядка 0,1 нм. Решение. Неопределенность в координате электрона Dх £ 1 = 0,1 нм, тогда Dvх ³ h/ml» 106 м/с. Скорость же электрона найдем из условия Бора о том, что в первой орбите электрона должна укладываться одна длина волны, т. е. l = 2pr = h/mv; v = h/mr @ 106м/c, т. е. v» Dv. 59. Оценить минимальную кинетическую энергию электрона, локализованного в области размером l = 0,1 нм. Решение.
» 150 Эв. 60. Электрон с кинетической энергией Т = 10 Эв локализован в области размером l = 1 мкм. Оценить относительную неопределенность скорости электрона. 61. Оценить минимальную энергию Еmin гармонического осциллятора, имеющего массу m (потенциал U=kx2/2, частота w=(k/m)1/2), используя соотношение неопределенности. 62. Оценить с помощью соотношения неопределенности энергию связи электрона в основном состоянии атома водорода и соответствующее расстояние электрона до ядра.
Решение. Энергия электрона Е = Так как r - размер области локализации электрона, для оценки р имеем р~h/r. Е @ Найдем min этого выражения: (¶Е/¶r) = 0.
Есв ~-mе4/2h2 = - 13,6 Эв. 63. Оценить минимальную возможную энергию электронов в атоме Не и соответствующее расстояние от электрона до ядра. Решение. Обозначим заряд ядра Ze, а размеры областей локализации электронов - r1 и r2. Тогда для оценки импульсов имеем: p1 ~ h/r1; p2 ~ h/r2, так что кинетическая энергия электрона -
Примечание: Минимальная возможная энергия электрона будет тогда, когда минимальна энергия кулоновского отталкивания электронов, т.е. когда электроны атома будут находиться на максимально возможном расстоянии друг от друга. Эта энергия отталкивания соответствует оценке
Для полной энергии электронов, поэтому справедлива оценка. Е(r1; r2) = Считая r1 = r2 и используя (¶ Е /¶ r1) = 0, находим:
где величина 13,6эВ=
Ответ: -83,3 эВ 64. Атом испустил фотон с длиной волны l=600 нм за время t=18-8 с. Оценить неопределенность Dх, с которой можно установить координату фотона в направлении его движения, а также относительную неопределенность его длины волны. Решение. Dх~сt = 3 м; (Dl/l) = сt/l; DЕDt = hct/Dl ³ h; Dl £ сt. 65. Монохроматический параллельный пучок электронов нормально падает на диафрагму с энергией Е=100 Эв, в которой узкая щель (рис. 5). На расстоянии L=100 см от диафрагмы расположен экран. Оцените ширину щели, при которой ширина изображения на экране будет минимальной. Решение. Пусть b - ширина щели, а D¢ - уширение, связанное с неопределенностью импульса Dру, вызванного дифракцией прохождения через щель. Положив Dу» b,имеем:
p = D¢ = Lq = L D = D¢ + b = b +
Dр р q D

Е b b
L
Рис. 5.
66. Проверьте принцип неопределенности на примере основного состояния электрона в одномерной прямоугольной яме с бесконечно высокими стенками. 67. Пользуясь принципом неопределенности, оцените энергию основного состояния иона Li+. 68. Какая возникает неопределенность в энергии частицы массой m при ее локализации в области размером l см? 69. Частица массой m движется в одномерной прямоугольной яме шириной l с бесконечно высокими стенками. Неопределенность в координате частицы Dх = l, импульс же частицы известен точно из ее полной энергии. Не противоречит ли это неравенству Гейзенберга? 70. Не противоречит ли принципу неопределенности состояние электрона в атоме с нулевым моментом количества движения? Указание. Чтобы ответить на вопрос, запишите выражение для оператора кинетической энергии электрона, движущегося в поле центральных сил, в сферической системе координат. 71. Оцените величину кулоновского отталкивания электронов в атоме Не. 72. Два атома водорода сближаются из бесконечности на конечное расстояние. Как изменяются уровни энергии в системе?
|
||||||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 335; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.84.155 (0.031 с.) |
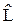 . Запишем разложение:
. Запишем разложение: . (1)
. (1) ,
, - собственные функции оператора
- собственные функции оператора 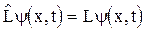 .
.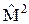 и
и  электрона в атоме является функция:
электрона в атоме является функция: .
. , где Dl - неопределенность в де бройлевской длине волны частицы, имеющая порядок Dl»b. Чем меньше шири-
, где Dl - неопределенность в де бройлевской длине волны частицы, имеющая порядок Dl»b. Чем меньше шири-
 Х р’
Х р’ р j
р j
 . Неопределенность в координате частицы Dl» b. Отсюда:
. Неопределенность в координате частицы Dl» b. Отсюда: q
q , где d - расстояние между щелями. Это значит, что в соответствии с принципом неопределенности измерение вносит неопределенность Dpx в px- проекцию импульса
, где d - расстояние между щелями. Это значит, что в соответствии с принципом неопределенности измерение вносит неопределенность Dpx в px- проекцию импульса . Но условие того, что дифракционная картина не разрушится, состоит в следующем: Dр¢х << pQ, где Dр¢х» h/l, а l - де Бройлевской длина волны частицы; причём Q = l/d. Таким образом, Dр¢х<<h/d, а вносимая индикатором неопределенность - Dрх >> Dр¢х, то есть много больше той, при которой дифракционная картина сохранилась бы.
. Но условие того, что дифракционная картина не разрушится, состоит в следующем: Dр¢х << pQ, где Dр¢х» h/l, а l - де Бройлевской длина волны частицы; причём Q = l/d. Таким образом, Dр¢х<<h/d, а вносимая индикатором неопределенность - Dрх >> Dр¢х, то есть много больше той, при которой дифракционная картина сохранилась бы. ,
,
 .
. .
. ; rmin =
; rmin =  =a=0,529
=a=0,529  - радиус первой Боровской орбиты.
- радиус первой Боровской орбиты. .
. .
.
 13,6 эВ,
13,6 эВ, постоянная Ридберга. Так как Z=2,то
постоянная Ридберга. Так как Z=2,то эВ. Эксперимент даёт -79 эВ.
эВ. Эксперимент даёт -79 эВ. ; Dр» h/b,
; Dр» h/b, ,
, » 2b = 8,8 мкм,
» 2b = 8,8 мкм, = 0;
= 0;  ; b =
; b =  » 4,4 мкм.
» 4,4 мкм. D’
D’


