
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Идеальные газы и основные газовые законыСодержание книги
Поиск на нашем сайте
Оглавление Введение……………………………………………………………….4 1. Техническая термодинамика…………………………………… 5 1.1. Идеальные газы и основные газовые законы………………………….5 1.2. Газовые смеси……………………………………………………………8 1.3. Теплоемкость газов………………………………………………….…12 1.4. Основные функции состояния рабочего тела. Первый закон термодинамики………………………………………………………………...15 1.5. Основные процессы изменения состояния идеальных газов………..20 1.6. Второй закон термодинамики…………………………………………29 1.7. Примеры решения задач……………………………………………….35 1.8. Контрольные задания к разделу 1……………………………………..46 2. Реальные газы. Водяной пар. Влажный воздух……………..50 2.1. Процессы получения и изменения состояния водяного пара………..51 2.2. Параметры влажного воздуха. J-d диаграмма влажного воздуха……54 2.3. Процессы истечения и дросселирования газов и паров...……………58 2.4. Циклы паросиловых установок………………………………………..64 2.5. Примеры решения задач……………………………………………….73 2.6. Контрольные задания к разделу 2…………………………………….76 3. Теплообменные процессы………………………………………..77 3.1. Теплопроводность………………………………………………………77 3.2. Конвективный теплообмен и теплопередача…………………………84 3.3. Лучистый теплообмен………………………………………………….90 3.4. Теплообменные аппараты…………………………………….………..93 3.5. Примеры решения задач……………………………………………….94 3.6. Контрольные задания к разделу 3…………………………………….102 4. Массообменные процессы……………………………...……….105 4.1. Общие понятия…………………………………………………………106 4.2. Основные уравнения массообменных процессов……………………108 4.3. Совместные процессы тепло и массообмена……………………..….110 4.4. Расчет тепло – массообменных аппаратов…………….……………..117 4.5. Примеры решения задач………………………………………………125 4.6. Контрольные задания к разделу 4………….…………………………132 Приложения………………………………………………………….134 Приложение 1.Множители и приставки для образования десятичных кратных и дольных единиц и их наименование ……………………………134 Приложение 2. Международная система единиц (СИ)…………………..134 Приложение 3. Молекулярные массы, плотности при нормальных
условиях и газовые постоянные некоторых газов……………………..…...135 Приложение 4. Насыщенный водяной пар (по температурам)………….135 Приложение 5. Насыщенный водяной пар (по давлениям)…………..…136 Приложение 6. I-d диаграмма влажного воздуха……………………...…139 Приложение 7. Физические свойства воды на линии насыщения...……140 Приложение 8.Физические свойства сухого воздуха………………...…141 Приложение 9.Термодинамические свойства воды и водяного пара в состоянии насыщения…………………………………………...………….142 Введение Тепло- и массообменные процессы происходят практически во всех аппаратах инженерных сетей, обеспечивающих создание и поддержание требуемых параметров микроклимата. Знание теоретических основ термодинамики, тепловых и массообменных процессов необходимо для решения задач, связанных с проектированием и эксплуатацией систем теплоснабжения и отопления, водоснабжения и водоотведения, вентиляции и кондиционирования воздуха. Поэтому изучение тепло- и массообменных процессов необходима для студентов специальностей «теплогазоснабжение и вентиляция», «городское строительство и хозяйство», промышленное и гражданское строительство», «водоснабжение и водоотведение» по направлению подготовки Строительство (270800.62). Для студентов по направлению подготовки Техносферная безопасность (280700.62) изучение тепловых и массообменных процессов необходимо для осуществления контроля безопасной эксплуатации теплообменных, теплогенерирующих аппаратов, котельных агрегатов, сушильных установок и другого оборудования с целью инженерной защиты окружающей среды. Основное назначение учебного издания – помочь студентам выработать навыки применения теории в решении конкретных задач. Каждый раздел включает теоретическую часть, в которой приведены основные формулы, определения и справочные сведения, необходимые для решения задач. Рассмотрены примеры решения наиболее типичных задач и даны задания для самостоятельного изучения. Причем, в пособии представлены задания различной сложности. Задания с одной звездочкой обязательны для студентов квалификации подготовки – бакалавр, с двумя звездочками – для подготовки специалистов, с тремя звездочками – для магистров.
Техническая термодинамика Газовые смеси Под газовой смесью понимается смесь газов, не вступающих между собой в химические реакции. Составляющие смесь отдельные газы называются компонентами. Каждый компонент смеси распространяется по всему объему смеси. Давление, которое имел бы каждый компонент, входящий в состав смеси, если бы он находился один в том же объеме и при той же температуре, что и смесь, называется парциальным давлением компонента (от латинского pars – часть). По закону Дальтона давление смеси равно сумме парциальных давлений ее компонентов, т. е.:
Pсм = P1 + P2 + P3 +... + Pn =
где Рсм – давление газовой смеси; Р1, Р2, Р3, Рn – парциальные давления компонентов смеси. Итак, каждый компонент смеси, занимая весь объем смеси, находится под своим парциальным давлением. Но если этот компонент поместить под давлением Рсм при той же температуре смеси Tсм, то он займет объем Vi меньший, чем объем Vсм. Этот объем Vi называют приведенным или парциальным. Объем смеси равен сумме парциальных объемов ее компонентов:
V = V1 + V2 + V3 + … + Vn =
где V – полный объем смеси газов, м3; V1, V2, V3,…,Vn – парциальные объемы компонентов, м3, приведенные к условиям смеси, т. е. Рсм и Тсм. Состав газовой смеси чаще всего задается массовым или объемным способом. Массовая доля определяется отношением массы отдельного газа, входящего в смесь, к массе всей смеси:
где М1, М2, М3, …, Мn - масса отдельных газов, кг и М – масса всей смеси, кг. Объемной долей газа называют отношение объема каждого компонента, входящего в смесь, к объему всей газовой смеси при условии, что объем каждого компонента отнесен к давлению и температуре смеси (приведенный объем):
где V1, V2, V3, …, Vn – приведенные объемы компонентов газов, входящих в смесь, м3; V – общий объем газовой смеси, м3. Очевидно, что:
M1+M2+M3+…+Mn = M,
m1+m2+m3+…+mn = 1,
а также: V1+V2+V3+…+Vn = V,
r1+r2+r3+…+rn = 1.
Для перевода массовых долей в объемные пользуются формулой:
Перевод объемных долей в массовые производится по формуле:
Плотность смеси определяется из выражения:
или, если известен массовый состав, по формуле:
Удельный объем смеси представляет величину, обратную ρсм, поэтому, если дан объемный состав смеси, то:
Если же известен массовый состав, то:
Из уравнения (1.17) легко получается значение так называемой кажущейся молекулярной массы газовой смеси:
или через массовый состав:
Таблица 1.2. Теплоёмкость газов Теплоемкостью (точнее удельной теплоемкостью) называют количество теплоты, которое необходимо сообщить телу (газу), чтобы изменить температуру какой-либо количественной единицы на 1° С (1К). Количество теплоты в системе СИ измеряют в Дж или кДж. В зависимости от количественной единицы вещества различают массовую теплоемкость С – кДж/(кг·К), объемную теплоемкость С’–кДж/(м3·К) и киломольную теплоемкость μС – кДж/(кмоль·К). Поскольку в 1 м3 в зависимости от параметров состояния содержится различная масса газа, то объемную теплоемкость всегда относят к 1 м3 газа при нормальных условиях (РН = 760 мм рт. ст., tН = 0° С). Массовая, киломольная и объемная теплоемкости связаны между собой следующими зависимостями:
где μ – молекулярная масса или количество кг в киломоле данного вещества, кг/кмоль;
где 22,4 – объем киломоля любого идеального газа в нормальных физических условиях (следствие из закона Авогадро), м3н /кмоль;
C’= С·ρн, (1.29)
где ρН – плотность данного вещества при нормальных условиях, кг/м3н. Теплоемкость идеальных газов зависит от атомности, характера процесса и температуры. Теплоемкость реальных газов, кроме перечисленных выше факторов, зависит еще и от давления. Зависимость теплоемкости от температуры обычно выражают формулой:
C = a + bt + et2, (1.30)
где t–температура в °С; a, b, е – численные коэффициенты, определяемые экспериментально. Аналогичные зависимости получены не только для массовых, но и для других видов теплоемкости (объемных, киломольных). Различают среднюю и истиннуютеплоемкости. Средняятеплоемкость в интервале температур t1 – t2 равна:
где q1-2 – количество теплоты, подведенное в данном процессе, кДж/кг; t1, t2 – температура в начале и в конце процесса, °С. Если выражение (1.31) записать для бесконечно малого количества теплоты dq и интервала температур dt, то получим формулу так называемой истинной теплоемкости С при данной температуре:
Из выражения (1.32) dq = Cdt, а для всего процесса 1–2 количество теплоты q1-2 будет равно:
Это же количество теплоты можно выразить через среднюю теплоемкость, что следует из (1.31):
Имеется еще одна формула для подсчета q1-2:
Применение этого выражения удобно при наличии таблиц средних теплоемкостей В некоторых случаях требуется, пользуясь таблицами средних теплоемкостей
В теплотехнике особое значение имеют два случая нагревания (охлаждения): при постоянном давлении (изобарный процесс) и при постоянном объеме (изохорный процесс). Обоим этим случаям соответствуют изобарные и изохорные теплоемкости, имеющие в обозначениях индексы «p» «v». Изобарные теплоемкости: Изохорные теплоемкости: Между теплоемкостями при постоянном давлении и постоянном объеме существует следующая зависимость: -для массовых теплоёмкостей:
-для мольных теплоемкостей:
Для приближенных расчетов и при невысоких температурах можно принимать следующие значения мольных теплоемкостей (табл. 1.3). В технической термодинамике большое значение имеет отношение теплоемкостей при постоянном давлении и постоянном объеме, обозначаемое буквой k и называемое показателем адиабаты:
Принимая теплоемкость постоянной, на основании данных табл. 1.3 можно получить для одноатомных газов k=1,67; для двухатомных газов k=1,4; для трехатомных газов k=1,29.
Таблица.1.3. Приближенные значения киломольных теплоемкостей газов при постоянном объеме и постоянном давлении (C = const)
Если в процессе участвуют М кг или Vн м3 газа, то подсчет количества тепла производится по формулам:
и:
Теплоемкость газовой смеси определяется на основании следующих формул: массовая теплоемкость смеси:
oбъемная теплоемкость смеси:
мольная теплоемкость смеси:
где i – номер компонента смеси; n – число компонентов смеси. В этих выражениях mi, ri – соответственно массовая и объемная доля i-го компонента газовой смеси;
Первый закон термодинамики В технической термодинамике используются три основные функции состояния: внутренняя энергия, энтальпия и энтропия. Эти функции зависят только от состояния рабочего тела, их изменение в ходе термодинамического процесса не зависит от хода процесса. Указанные функции обозначаются соответственно буквами U, u; I, i; S, s. Если функция относится к М кг рабочего тела, то она обозначается прописной буквой, если к 1 кг – то строчной буквой. Внутренняя энергия – функция состояния закрытой термодинамической системы, определяемая тем, что ее приращение в любом процессе, происходящем в этой системе, равно сумме теплоты, сообщенной системе, и работы, совершенной над ней. Если рабочее тело – идеальный газ, то внутренняя энергия зависит только от температуры. Для процесса идеального газа изменение внутренней энергии ∆u1-2 равно:
Приближенная формула (
Условно принимают, что при нормальных условиях (t = 0o C) внутренняя энергия равна 0, тогда в данном состоянии, характеризуемом температурой t, внутренняя энергия u равна:
Приближенная формула (
ЭНТАЛЬПИЯ ГАЗОВ Заменяя в основном уравнении первого закона:
Величину pdv через d (pv) – vdp, получаем:
Выражение u+ pv является параметром состояния. В технической термодинамике этот параметр называют энтальпией и обозначают буквой i. Таким образом,
и, следовательно, основное уравнение первого закона, выраженное через энтальпию, имеет вид:
Для идеальных газов:
Следовательно,
где В теплотехнических расчетах обычно требуется знать изменение энтальпии, а не ее абсолютное значение, поэтому начало отсчета (0 К или 0о С) для конечного результата (
Интегрируя уравнение (1.50) при P = const, получаем:
Таким образом, количество тепла в процессе Р=const численно можно определить как разность энтальпии конечного и начального состояния.
ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ Первый закон термодинамики устанавливает эквивалентность при взаимных превращениях механической и тепловой энергии и математически может быть выражен следующим образом:
Q=L, (1.53)
где Q – количество тепла, превращенного в работу; L – работа, полученная за счет тепла Q. Количества тепла Q и работы L измерены в данном случае в соответствии с системой единиц СИ – в одних и тех же единицах – в джоулях. Существуют другие внесистемные единицы измерения соотношение между которыми приведены в табл. 1.4. Джоуль (Дж) – единица измерения механической работы (энергии) в системе единиц СИ представляет собой работу, совершаемую силой, равной 1 Н, на пути в 1 м, пройденном телом под действием этой силы по направлению, совпадающему с направление силы. Логическим следствием закона сохранения и превращения энергии является целесообразность измерения всех видов энергии одной и той же единицей. Поэтому за единицу измерения тепловой энергии также принимают джоуль, который представляет собой такое ее количество, которое появляется в результате превращения механической работы 1 Дж в тепло. Так как за единицу работы принят Дж, то единицей мощности будет являться Дж/сек. Эта единица носит название ватт (Вт). В технике применяют более крупные единицы энергии (работы) и мощности: кило джоуль (кДж), мегаджоуль (МДж), киловатт (кВт), мегаватт (МВт), киловатт-час (кВт·ч). Таблица 1.4. Второй закон термодинамики Второй закон термодинамики определяет направление, в котором протекают процессы, устанавливает условия преобразования тепловой энергии в механическую, а также определяет максимальное значение работы, которая может быть произведена тепловым двигателем. Второй закон термодинамики математически может быть выражен следующим образом:
Таблица. 1.5 Примеры решения задач Примеры решения задач к разделу 1.1 1. Давление в паровом котле P = 0,4 бар при барометрическом давлении B1 = 725 мм рт. ст. Чему будет равно избыточное давление в котле, если показание барометра повысится до B2 = 785 мм. рт. ст., а состояние пара в котле останется прежним? Барометрическое давление приведено к 00.
Решение Абсолютное давление в котле
Избыточное давление при показании барометра В2 = 785 мм рт. ст.
2. Во сколько раз объем определенной массы газа при -200 С меньше, чем при +200 С, если давление в обоих случаях одинаковое?
Решение При постоянном давлении объем газа изменяется по уравнению (1.9):
следовательно,
3. Баллон с кислородом емкостью 20 л находится под давлением 10 МПа при 150 С. После израсходования части кислорода давление понизилось до 7,6 МН/м2, а температура упала до 100 С. Определить массу израсходованного кислорода.
Решение Из характеристического уравнения:
PV = MRT
Имеем:
Следовательно, до расходования кислорода масса его составляла:
а после израсходования:
Таким образом, расход кислорода: 2,673 – 2,067 = 0,606 кг. 4. Сосуд емкостью V=10 м3 заполнен 25 кг углекислоты. Определить абсолютное давление в сосуде, если температура в нем t = 270 C.
Решение Из характеристического уравнения
PV = MRT
Имеем
Примеры решения задач к разделу 1.2 1. Атмосферный воздух имеет примерно следующий массовый состав: Определить объемный состав воздуха, его газовую постоянную, кажущуюся молекулярную массу и парциальные давления кислорода и азота, если давление воздуха по барометру В =760 мм рт. ст. Решение По уравнению (1.15) получаем
Газовая постоянная воздуха определяется по уравнению (1.23):
Кажущаяся молекулярная масса смеси определяется из уравнения (1.21):
или из уравнения (1.24):
Отсюда:
Парциальные давления определяем из уравнения (1.26):
следовательно,
2. Смесь газов состоит из водорода и окиси углерода. Массовая доля водорода Определить газовую постоянную смеси и ее удельный объем при нормальных условиях.
Решение Из уравнения (1.23):
Удельный объем газовой смеси найдем из характеристического уравнения Pυ = RT:
Примеры решения задач к разделу 1.3 1. Воздух в количестве 6м3 при давлении р1=3 бар и температуре t1 = 25o C нагревается при постоянном давлении до t2= 130о С. Определить количество подведенного к воздуху тепла, считая с = const. Для данного случаяиспользуем формулу (1.69):
Масса газа определится из уравнения (1.5):
а объем газа при нормальных условиях – из уравнения (1.11):
На основании формул (1.27) и (1.28) и табл. 1.3 имеем:
Следовательно,
или:
Примеры решения задач к разделу 1.4 1. В котельной электрической станции за 20 ч работы сожжены 62 т каменного угля, имеющего теплоту сгорания 28900 кДж/кг (6907 ккал/кг). Определить среднюю мощность станции, если в электрическую энергию превращено 18% тепла, полученного при сгорании угля. Решение Количество тепла, превращенного в электрическую энергию за 20 ч работы:
Эквивалентная ему электрическая энергия или работа:
Следовательно, средняя электрическая мощность станции:
2. Паросиловая установка мощностью 4200 кВт имеет к.п.д. Определить часовой расход топлива, если его теплота сгорания:
Решение По формуле (1.54):
отсюда:
Часовой расход топлива составит:
G= Примеры решения задач к разделу 1.5 1. В закрытом сосуде заключен газ при разрежении P1=50 мм. рт. ст. и температуре t1= 70o C. Показание барометра – 760 мм. рт. ст. До какой температуры нужно охладить газ, чтобы разрежение стало равным P2 = 100 мм. рт. ст.?
Решение Так как процесс происходит при V=const, то согласно формуле (1.61):
Подставляя значения, получаем:
отсюда:
2. В закрытом сосуде емкостью Принимая теплоемкость воздуха постоянной, определить, какое давление и какая температура устанавливается после этого в сосуде.
Решение Пользуясь уравнением состояния, определяем массу воздуха в сосуде:
Количество тепла, отводимого от воздуха в процессе, определяется уравнением (1.63):
откуда:
Значение Из соотношения параметров в изохорном процессе:
Имеем:
3. 1 кг воздуха при температуре Определить конечный объем, затрачиваемую работу и количество тепла, отводимого от газа. Решение Определяем начальный объем воздуха из уравнения состояния:
Так как в изотермическом процессе:
то конечный объем
Работа, затрачиваемая на сжатие 1 кг воздуха, получается из уравнения (1.73):
Количество тепла, отводимого от газа, равно работе,
4. 1 кг воздуха при начальной температуре Определить конечный объем, конечную температуру и затрачиваемую работу. Решение Из соотношения параметров в адиабатном процессе по уравнению (1.82) находим:
откуда:
Принимая k = 1,4, получаем:
Затраченная работа по уравнению (1.85):
Конечный объем определяется из уравнения состояния:
5. 1 кг воздуха при P1 = 5 бар и t1 = 111o C расширяется политропно до давления P2 = 1 бар. Определить конечное состояние воздуха, изменение внутренней энергии, количество подведенного тепла и полученную работу, если показатель политропы n = 1,2.
Решение Определяем начальный удельный объем воздуха:
Конечный удельный объем воздуха находим из уравнения (1.96):
Конечную температуру проще всего найти из характеристического уравнения:
Величину работы находим из уравнения (1.102):
Изменение внутренней энергии:
Количество тепла, сообщенного воздуху, по уравнению (1.109):
9. 1,5 кг воздуха сжимают политропно от P1 = 0,9 бар и t1 =18o C до P2 = 10 бар; температура при этом повышается до t2 = 125o C. Определить показатель политропы, конечный объем, затраченную работу и количество отведенного тепла.
Решение По формуле (1.115):
отсюда:
Конечный объем определяем из характеристического уравнения:
Затраченная работа по уравнению (1.107):
Количество отведенного тепла по уравнению (1.110):
Примеры решения задач к разделу 1.6 1. Определить энтропию 1 кг кислорода при P=8 бар и t=250о С. Теплоемкость считать постоянной.
Решение По формуле (1.121):
Так как для двухатомных газов R = 8,314 кдж/(кмоль
2. 1 кг кислорода при температуре t1 = 127o C расширяется до пятикратного объема; температура его при этом падает до t2 = 27o C. Определить изменение энтропии. Теплоемкость считать постоянной.
Решение По уравнению (1.123):
3. 10 м3 воздуха, находящегося в начальном состоянии при нормальных условиях, сжимают до конечной температуры 400о С. Сжатие проводится: 1) изохорно, 2) изобарно, 3) адиабатно и 4) политропно с показателем политропы n = 2,2. Считая значение энтропии при нормальных условиях равным нулю и принимая теплоемкость воздуха постоянной, определить энтропию воздуха в конце каждого процесса.
Решение Находим массу 10 м3 воздуха при нормальных условиях:
Определяем изменение энтропии в каждом из перечисленных процессов: 1) Изохорное сжатие:
2) Изобарное сжатие:
3) Адиабатное сжатие:
4) политропное сжатие:
1.8. Контрольные задания к разделу 1 Контрольные задания к разделу 1.1-1.2 1*. Разрежение в газоходе парового котла, измеряемое тягомером, равно Р мм вод. ст. Определить абсолютное давление газов, если показание барометра 730 мм рт. ст., и выразить его в МПа. 2*. Объемный состав газообразного топлива следующий: H2, %, CH4, %. Определить среднюю молекулярную массу и газовую постоянную смеси.
3*. Определить массу 5 м3 водорода 5 м3 кислорода и 5 м3 углекислоты при давлении P бар и температуре 1000 С. 4*. Какова будет плотность окиси углерода при t0 С и 710 мм рт. ст., если при 00 C и 760 мм рт. ст. она равна 1,251 кг/м3? 5*. Дымовые газы, образовавшиеся в топке парового котла, охлаждаются с t0 С до 2500 С. Во сколько раз уменьшается их объем, если давление газов в начале и конце газоходов одинаково? 6**.. В цилиндрическом сосуде диаметром d м; и высотой h=2,4 м находится воздух при t 0С, давление воздуха Pmax=0,865 МПа, Рбар=101858 Па. Определить массу воздуха в сосуде и плотность. 7**. В резервуаре объемом 10 м3 находится газовая смесь, состоящая из n1 кг кислорода и n2 кг азота. Температура смеси равна 27 °С. Определить парциальные давления компоненто
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 183; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.13.192 (0.016 с.) |

 , (1.13)
, (1.13) , (1.14)
, (1.14)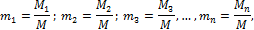
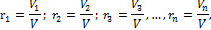
 (1.15)
(1.15) . (1.16)
. (1.16) (1.17)
(1.17) , кг/м3. (1.18)
, кг/м3. (1.18) (1.19)
(1.19) (1.20)
(1.20) , (1.21)
, (1.21) (1.22)
(1.22)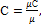 (1.27)
(1.27) (1.28)
(1.28) , (1.31)
, (1.31) . (1.32)
. (1.32) . (1.33)
. (1.33) . (1.34)
. (1.34)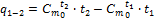 . (1.35)
. (1.35) .
. . Для этого из (1.34) и (1.35) можно получить формулу:
. Для этого из (1.34) и (1.35) можно получить формулу: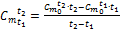 . (1.36)
. (1.36)
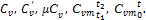
 , (1.37)
, (1.37) . (1.38)
. (1.38) . (1.39)
. (1.39) , (1.40)
, (1.40) . (1.41)
. (1.41) (1.42)
(1.42) (1.43)
(1.43) (1.44)
(1.44) ,
, 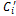 ,
,  – соответственно массовая, объемная и мольная теплоемкость i-го компонента;
– соответственно массовая, объемная и мольная теплоемкость i-го компонента;  ,
,  ,
, 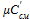 – соответственно массовая, объемная и мольная теплоемкость газовой смеси.
– соответственно массовая, объемная и мольная теплоемкость газовой смеси.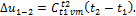 (1.45)
(1.45)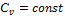 ):
):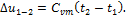 (1.46)
(1.46) (1.47)
(1.47) ):
): (1.48)
(1.48) .
.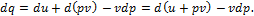
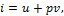 (1.49)
(1.49)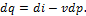 (1.50)
(1.50)
 (1.51)
(1.51)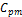 – средняя массовая теплоемкость при постоянном давлении в пределах от 0 до T.
– средняя массовая теплоемкость при постоянном давлении в пределах от 0 до T.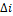 ) не имеет значения.
) не имеет значения. (1.52)
(1.52) (1.117)
(1.117)






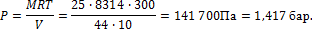
 = 23,2%;
= 23,2%;  = 76,8%.
= 76,8%.


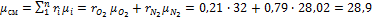 ,
,

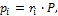




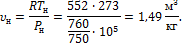





 ,
,

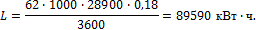

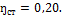

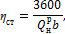





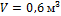 содержится воздух при давлении
содержится воздух при давлении  и температуре
и температуре  В результате охлаждения сосуда воздух, содержащийся в нем, теряет 105 кДж.
В результате охлаждения сосуда воздух, содержащийся в нем, теряет 105 кДж.


 полученно из выражения
полученно из выражения  (для двухатомных газов).
(для двухатомных газов). .
.
 и начальном давлении
и начальном давлении  сжимается изотермически до конечного давления
сжимается изотермически до конечного давления 
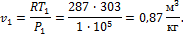

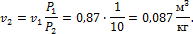



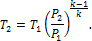





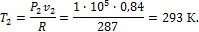





 .
.

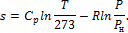
 , а
, а град), то:
град), то: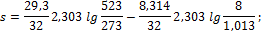
 .
.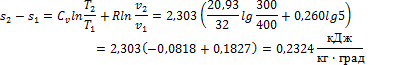


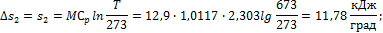

 .
.


