
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение перемещений в статически определимых системах
Для заданных схем балок и рам (рис 5.1 и 5.2) с размерами и нагрузками приведенными в таблице 8, которые отвечают шифру студента по формуле Мора или по правилу Верещагина О.М., необходимо: - построить изогнутую ось балки и вычислить угол поворота на консоли; - для схемы ломаного бруса (рамы) определить линейное перемещение поперечного сечения А и угол поворота поперечного сечения В.
Таблица 8
Рисунок 5.1
Рисунок 5.2 Пример. Для заданной схемы балки (рис. 5.3) построить изогнутую ось балки и определить угол поворота в точке D, EIz - const.
1 Строим эпюру моментов от действия внешней нагрузки МF. SM A = 0, RB×10 + 8 - 15×12 - 2×2×11 = 0, RB = 21,6 кH. SM B = 0, RA×10 - 8 + 15×2 + 2×2×1 = 0, RA = - 2,6 кH. SY = 0, -2,6 + 21,6 -2×2 - 15 = 0.
0≤ x 1 ≤10 м MF=-8-2,6×x1, x1=0, MF=-8 кНм, x1=5м, MF=-21 кНм, x1=10м, MF=-34 кНм.
0≤ x 2 ≤2 м MF=-15х2-2x2(х2/2) =-15х2- x2=0, MF= 0, x2=1м, MF=-16 кНм, x2=2м, MF=-34 кНм. 2 Построение линии прогибов. Для этого определяем перемещения в вертикальном направлении для характерных точек С и D. а) в точке С прикладываем силу F = 1 рис. 5.3(а). От действия этой силы строим эпюру RA = RB = 0,5.
0≤ x 3 ≤5 м
Рисунок 5.3 x3=0,
Определяем перемещение в точке С путем перемножения эпюры MF и
б) в точке D прикладываем силу F=1 см. рис. 5.3(б). От действия этой силы строим эпюру
0≤ x 4 ≤10 м 0≤ x 5 ≤2 м
x4 = 0, x4 = 10 м, Перемножая эпюры MF и
Для построения изогнутой оси балки проводим линию, параллельную оси балки и в выбранном масштабе откладываем полученные значения перемещений в точках С и D. Необходимо помнить, если перемещение со знаком минус, то оно откладывается в направлении, противоположном единичной силе, а на опорах А и В вертикальные перемещения равняются нулю. Соединив плавной кривой полученные четыре точки получим изогнутую ось балки или линию изгиба см. рис. 5.3(в).
3 Вычисляем угол поворота в точке D. Для этого прикладываем единичный момент М = 1 в этой точке и строим эпюру SМВ = 0, -
0≤ x 6 ≤10 м 0≤ x 7 ≤2 м
x6 = 0, x6 = 10,
Перемножив эпюры MF и
Знак «плюс» указывает на то, что поворот сечения в точке D осуществляется по часовой стрелке, то есть в направлении единичного момента.
Последовательность решения этой задачи такая же, как и в предыдущем примере. 1 Определяем опорные реакции и строим эпюру от внешней нагрузки MF (рис.5.5). ∑X=0, - Hc - 70·5 = 0, Hc = - 350 кН.
∑ М c =0, -RB·5+70·5·2,5+70·3,6·1,8 = 0, RВ = 266 кН.
Рисунок 5.4 ∑Y=0,
0≤x 1 ≤3,6м
 , ,
0≤x 2 ≤5м
MF=-266·x2,
0≤ y 1 ≤5 м
 ), ),
Рисунок 5.5
2 Вычисляем линейное вертикальное перемещение в точке А (рис.5.6). Для этого в точке А прикладываем вертикально силу F = 1 и от ее действия строим эпюру
RB×5 - 1×3,6 = 0, RB = 0,72.
SY = 0, -RC + 0,7 + 1 = 0, RC = 1,72. 0≤ x 1 ≤3,6 м
x1=0, x1=3,6м, 0≤ x 2 ≤5 м
x2=0, x2=5м,
Рисунок 5.6 Знак ²минус² указывает на то, что перемещение сечения в точке А происходит в направлении, противоположном единичной силе.
3 Определяем угол поворота поперечного сечения в точке В. Для этого в точке В прикладываем момент М = 1 и строим эпюру SM C = 0, RB×5 - 1 = 0, RB = 0,2. S M В = 0, НC×5 - 0,2×5 + 1 = 0, НC = 0.
0≤ x 1 ≤5 м
x1=5м,
То есть поворот сечения на опоре В происходит по часовой стрелке.
КОНТРОЛЬНОЕ ЗАДАНИЕ № 9 Определение перемещений Для заданной схемы рамы (рис. 5.8) найти вертикальное перемещение сечения А - Vа и угол поворота сечения В - Өв от действия равномерно распределенной нагрузки с интенсивностью - g и сосредоточенной силой F = Данные берем из таблицы 9. Таблица 9
Рисунок 5.8
1. Строим эпюру от внешней нагрузки М F (рис 5.10) 0 ≤ x1 ≤ 2,9м
0 ≤ y1 ≤ 2,9м
Рисунок 5.9
0 ≤ x2 ≤ 2,4м МF =62·2,9- x2 = 0 М F = -38,8 кН·м x2 = 2,4м М F = -550,5 кН·м 2. Вычисляем вертикальное пере-мещение в точке А-Vа. Для этого в точке А прикладываем вертикально силу F = 1 и от ее действия строим эпюру умножаем на эпюру МF на Рисунок 5.10 одноименных элементах.
Рисунок 5.11 0 ≤ Х1 ≤ 2,4м
При перемножении эпюр используем правило Верещагина.
Знак „минус” указывает на то, что перемещение сечения в точке А происходит в направлении противоположном единичной силе. 3 Определяем угол поворота поперечного сечения в точке В. Для этого в точке В прикладываем момент М = 1 и строим эпюру Для определения угла поворота сечения - Өв, перемножаем эпюры М F (рис. 5.10) и
Рисунок 5.12 0 ≤ Х2 ≤ 5,3м __ МВ = +1
То есть поворот сечения в точке В происходит по часовой стрелке.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 869; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.197.198 (0.058 с.) |



 ,
, .
. = 0, x3=5м,
= 0, x3=5м,  на одноименных участках по правилу Верещагина с использованием таблицы 1.
на одноименных участках по правилу Верещагина с использованием таблицы 1.
 .
. SМВ = 0,
SМВ = 0,  ,
, 
 определяем перемещение в точке С.
определяем перемещение в точке С.
 ,
, 
 , определяем угол поворота сечения в точке D.
, определяем угол поворота сечения в точке D.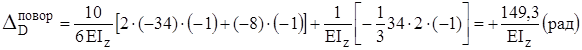
 Пример. Для заданной схемы рамы (рис.5.4) определить линейное перемещение поперечного сечения А и угол поворота поперечного сечения В.
Пример. Для заданной схемы рамы (рис.5.4) определить линейное перемещение поперечного сечения А и угол поворота поперечного сечения В.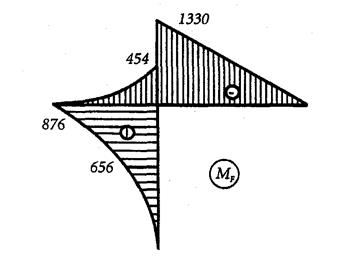 -RC-70·3,6-266 = 0, RC = 518 кН.
-RC-70·3,6-266 = 0, RC = 518 кН. . Полученную эпюру
. Полученную эпюру  SM C = 0,
SM C = 0, = 1×х1,
= 1×х1,


 (рис. 5.7). Для определения угла поворота сечения перемножаем эпюры MF и
(рис. 5.7). Для определения угла поворота сечения перемножаем эпюры MF и 

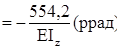
 .
.
 Пример. Для заданной рамы (рис. 5.9) вычислить вертикальное перемещение сечения А-Vа и угол поворота сечения В - Өв .
Пример. Для заданной рамы (рис. 5.9) вычислить вертикальное перемещение сечения А-Vа и угол поворота сечения В - Өв . МF=-52
МF=-52  М F = -62 y1
М F = -62 y1 

 (рис. 5.11). Полученную эпюру
(рис. 5.11). Полученную эпюру 


 (рис. 5.12).
(рис. 5.12).




