
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Подбор сечения балки и проверка ее прочности
Для заданных схем балок (рис.3.3) с размерами и нагрузками, которые следует взять соответственно собственному шифру из таблицы 4, подобрать двутавровое сечение балки и для него выполнить проверку прочности по наибольшим напряжениям, а также в опасном сечении балки для опасной точки сечения.
Таблица 4
Рисунок 3.3
КОНТРОЛЬНОЕ ЗАДАНИЕ № 5 Изгиб консольной балки
Для заданных схем балок (рис. 3.4) с размерами и нагрузками, которые следует взять соответственно собственному шифру из таблицы 5, необходимо: 1 Построить эпюры изгибающих моментов – Мz и поперечных сил – Qy. 2 Подобрать прямоугольное поперечное сечение, соотношение сторон которого известно, а расчетное сопротивление на изгиб равняется: R = 14 МПа = 1,4 кН/см2 3 Определить наибольшее касательное напряжение τmax.
Таблица 5
Рисунок 3.4
Пример. Для заданной балки (рис 3.5) построить эпюры Мz и Qy; подобрать прямоугольное поперечное сечение, соотношение сторон h/b = 1,4; расчетное сопротивление на изгиб R = 14 МПа = 1,4 кН/см2; определить наибольшее касательное напряжение τmax.
0 ≤х1≤ 1,2м
Qy= +8·х1 х1 = 0 Qy = 0 х1 =1,2м Qy =+9,6кН
Qy = 8·1,2 – 60 = - 50,4 кН
Рисунок 3.5
2 Подбираем прямоугольное поперечное сечение при h/b = 1,4 Rизг = 1,4 кН/см2
3 Определяем наибольшее касательное напряжение τ max (рис. 3.6).
Qymax = 50,4кН b = 26,6см
Рисунок 3.6
Szполусечение = 26,6·18,6·9,3 = 4601,3 см3
τmax = 0,08 кН/см2
КОНТРОЛЬНОЕ ЗАДАНИЕ №6 Изгиб однопролетной балки
Для заданных схем балок (рис. 3.7) с размерами и нагрузкой, которые следует взять соответственно собственному шифру из таблицы 6 необходимо: 1 Построить эпюры изгибающих моментов Mz и поперечных сил Qy. 2 Подобрать двутавровое поперечное сечение при расчетном сопротивлении R = 220 МПа = 22кН/см2 3 Проверить прочность балки на срез при Rсрез. = 130 МПа = 13кН/см2
Рисунок 3.7
Таблица 6
Пример. Для заданной балки (рис 3.8) построить эпюры Mz и Qy; подобрать двутавровое поперечное сечение при расчетном сопротивлении R = 22кН/см2; проверить прочность балки на срез Rсрез = 13кН/см2
1 Строим эпюры Qy и Mz. Определяем опорные реакции
∑Мв = 0 - Rа ·5,1+16·2,5·3,85+20·7,9=0 Rа = +61,2кН ∑Ма = 0 + Rв ·5,1-16·2,5·1,25+20·2,8=0 Rв = -1,2кН ∑Fу = 0 -20+61,2-16·2,5-1,2=0 0 ≤ x1 ≤ 2,6м
Mz = -1,2·х1 Qy= +1,2кН 0 ≤ x2 ≤ 2,8м
Mz = -20·х2 0 ≤ x3 ≤ 2,5м
2 Подбираем сечение двутаврового профиля при R = 22кН/см2
По сортаменту (приложение А) принимаем двутавр
3 Проверяем прочность на срез Rсрез = 13кН/см2
Условие прочности по касательным напряжениям выполняется.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 656; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.208.183 (0.015 с.) |


 1 Строим эпюры Qy и Мz с использованием правила знаков приведенного на рис. 1.8
1 Строим эпюры Qy и Мz с использованием правила знаков приведенного на рис. 1.8

 0 ≤ x2 ≤ 0,8м
0 ≤ x2 ≤ 0,8м Мz = - 8 · 1,2 (х2 + 0,6) + 60 х2 + 45
Мz = - 8 · 1,2 (х2 + 0,6) + 60 х2 + 45 см3
см3 ;
; 
 ; 0,3 b3 = 5682 см2
; 0,3 b3 = 5682 см2 см, b = 26,6см, h = 37,2см.
см, b = 26,6см, h = 37,2см.






 Qy= -20кН
Qy= -20кН Qy= -20+61,2-16· х3
Qy= -20+61,2-16· х3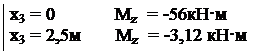 Mz = -20·(х3 +2,8)+61,2·х3 -
Mz = -20·(х3 +2,8)+61,2·х3 - 

 №22, у которого Iz = 2790см4, Szполусечение = 143 см3, d = 0,54 см.
№22, у которого Iz = 2790см4, Szполусечение = 143 см3, d = 0,54 см.




